Kryptologia postkwantowa
Jednym z ważniejszych osiągnięć informatyki opartej o komputer kwantowy, które zresztą eksponujemy w tym numerze Delty, jest opracowanie efektywnego (wielomianowego od rozmiaru danych) algorytmu na rozkład dużych liczb na czynniki pierwsze. Wspaniały, budzący zachwyt wynik. Nie dość, że przepiękny, korzystający z bardzo ładnego fragmentu matematyki, to jeszcze pozwalający wierzyć, że komputer kwantowy złożony z 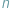 kubitów jest istotnie lepszy od komputera klasycznego, zawierającego pamięć o
kubitów jest istotnie lepszy od komputera klasycznego, zawierającego pamięć o 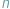 bitach. Albo inaczej: że (też prezentowany w tym numerze) model obliczeń komputera kwantowego ma istotnie większą siłę wyrazu (przy założeniu wielomianowego czasu działania) niż klasyczny model Turinga czy inne równoważne.
bitach. Albo inaczej: że (też prezentowany w tym numerze) model obliczeń komputera kwantowego ma istotnie większą siłę wyrazu (przy założeniu wielomianowego czasu działania) niż klasyczny model Turinga czy inne równoważne.
Co to znaczy w praktyce?
To znaczy, że wierzymy, iż istnieją problemy, które komputer kwantowy, mający 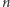 kubitów i wielomianowy od
kubitów i wielomianowy od  czas na działanie, rozwiąże, ale już komputer klasyczny, obdarzony analogicznymi zasobami (
czas na działanie, rozwiąże, ale już komputer klasyczny, obdarzony analogicznymi zasobami ( 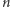 bitów pamięci i wielomianowy czas), im nie podoła. Hipotetycznym przykładem takiego problemu jest właśnie rozkład liczb na czynniki pierwsze. Dzięki Peterowi Shorowi wiemy, że komputer kwantowy radzi sobie z tym zadaniem. Z drugiej strony: nikt jeszcze nie potrafił pokazać, jak to zadanie rozwiązać (efektywnie) na komputerze klasycznym.
bitów pamięci i wielomianowy czas), im nie podoła. Hipotetycznym przykładem takiego problemu jest właśnie rozkład liczb na czynniki pierwsze. Dzięki Peterowi Shorowi wiemy, że komputer kwantowy radzi sobie z tym zadaniem. Z drugiej strony: nikt jeszcze nie potrafił pokazać, jak to zadanie rozwiązać (efektywnie) na komputerze klasycznym.
Wszystko, co powyżej, wydaje się tylko i wyłącznie zestawem dobrych wiadomości. Jednak nie do końca! W dziedzinie kryptologii istnienie lepszych niż klasyczne komputerów może powodować problemy. No bo przecież bezpieczeństwo większości protokołów kryptologicznych opiera się na założeniu, że jakiś problem jest bardzo trudny. Gdy nagle dostajemy nowe potężne narzędzie, może się przecież okazać, że pewne problemy nagle stają się już łatwe! Nie jest to wcale czcze gadanie, co od razu pokazuje algorytm Shora: przecież szyfrowanie RSA opiera się na trudności faktoryzacji, więc nie będzie ono miało sensu w świecie postkwantowym.
Kryptolodzy stoją więc przed konkretnym wyzwaniem. Chcąc przygotować świat na nadejście komputerów kwantowych, muszą projektować protokoły oparte na trudności problemów innych niż rozkład na czynniki pierwsze. Takie inne założenia w świecie kryptologów oczywiście istnieją: często zakładamy chociażby trudność problemu logarytmu dyskretnego (np. w protokole Diffiego-Hellmana), czy problemu logarytmu w grupie krzywych eliptycznych (np. w podpisie cyfrowym ECDSA). Niestety! Oba te założenia również potrafimy rozwiązywać efektywnie za pomocą (hipotetycznego) komputera kwantowego...
Czytelnik Pełen Obaw zapewne w tym miejscu zastanawia się, czy może nie jest przypadkiem tak, że po prostu komputer kwantowy zaatakuje skutecznie wszystkie potencjalne protokoły kryptologiczne, bo, na przykład, będzie potrafił rozwiązać szybko każdy problem z klasy NP. Większość badaczy nie jest jednak aż tak pesymistyczna w tym temacie. To znaczy, o ile wierzy się, że komputer kwantowy jest lepszy od klasycznego, to jednak intuicja informatyków powszechnie skłania ich ku hipotezie, że nie jest on w stanie szybko rozwiązywać problemów NP-zupełnych.
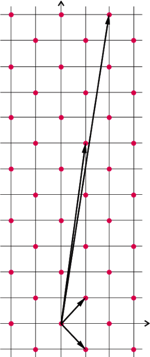
Powyższy pogląd daje nadzieję na bezpieczną kryptologię postkwantową. Co więcej, mamy już kandydatów na problemy, które wydają się trudne dla komputera kwantowego. Mamy także gotowy dość szeroki wachlarz konkretnych protokołów opartych na tych założeniach. Przykładów takich protokołów tutaj podawać tym razem nie będziemy, ale chcemy przynajmniej zaprezentować problem, który przyjmujemy jako trudny w świecie postkwantowym. (Co oznacza, że badacze tej dziedziny starają się redukować do niego inne protokoły.) Opowiemy o problemie najmniejszego wektora w kracie (shortest vector problem, w skrócie SVP).
Załóżmy, że mamy dane 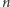 wektorów
wektorów 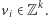 Kratą całkowitoliczbową rozpiętą przez te wektory nazywamy zbiór
Kratą całkowitoliczbową rozpiętą przez te wektory nazywamy zbiór
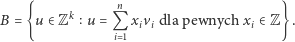
Pytamy teraz o najkrótszy (w sensie zwykłej metryki euklidesowej) niezerowy wektor w zbiorze 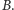 Problem ten (oczywiście dla odpowiednio dobranych parametrów
Problem ten (oczywiście dla odpowiednio dobranych parametrów 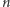 i
i 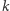 oraz umiejętnie wylosowanych wektorów
oraz umiejętnie wylosowanych wektorów 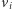 ) uchodzi za bardzo trudny nawet dla komputera kwantowego.
) uchodzi za bardzo trudny nawet dla komputera kwantowego.
Popatrzmy jeszcze przez chwilę na bardzo małe instancje problemu SVP. Proponuję dwie zagadki. Najpierw zerknijmy na zestaw: 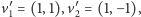 a następnie na:
a następnie na: 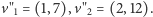
Pytamy, oczywiście, o najmniejszy niezerowy wektor w kratach rozpiętych przez te zestawy wektorów.
W pierwszym przypadku dość łatwo zauważyć (i udowodnić), że najmniejszymi wektorami (poza dwoma innymi, symetrycznymi względem zera) są właśnie wejściowe 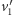 i
i 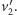 Co ciekawe, w drugiej zagadce, mimo że wejściowe wektory wyglądają groźniej, to rozpinana przez nie krata jest dokładnie tą samą kratą (czemu?), więc najmniejsze wektory to ponownie
Co ciekawe, w drugiej zagadce, mimo że wejściowe wektory wyglądają groźniej, to rozpinana przez nie krata jest dokładnie tą samą kratą (czemu?), więc najmniejsze wektory to ponownie 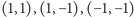 oraz
oraz 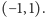
Podane przykłady mają na celu ilustrację jeszcze jednej własności problemu SVP. Otóż dla ustalonej kraty istnieją różne zestawy wektorów ją definiujące (tzw. bazy), co więcej: problem SVP dla różnych baz tej samej kraty może być istotnie trudniejszy. Czytelnik Domyślny, któremu kojarzy się to z kryptografią opartą o klucze prywatne i publiczne, nie myli się. Czytelnikowi Sumiennemu proponujemy znalezienie takich liczb całkowitych 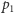 i
i 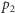 oraz
oraz 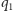 i
i 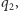 aby było
aby było
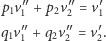
Odpowiedź jest tutaj.
PS. Czytelnik-Profan może być z kolei zaniepokojony nadużywaniem w tym tekście zwrotów takich jak wydaje się, pozwalający wierzyć itp. Nie jest to jednak przypadek, a o tym, że kryptologia to nauka dla ludzi dużej wiary, próbowałem przekonać Czytelników już w numerze 10/2017 Delty.
