Na szczęście, opracowałem pewien plan. Podzielę się tą informacją ze służbami specjalnymi. Wybrałem trzy: ABW, CIA i Mosad. Czy mogę jednak w pełni ufać służbom specjalnym? Chyba nie. Dlatego chcę dostarczyć im takie informacje, żeby żadna pojedyncza instytucja nie mogła samodzielnie odkryć nawet kawałka mojej tajemnicy. Co więcej, chcę to zrobić tak, by nawet dwie z nich, jeśli się potajemnie zmówią, nie zdołały odtworzyć ani litery z mojego sekretu. System musi być taki, że dopiero gdy wszystkie trzy służby udostępnią sobie dostarczone przeze mnie informacje, będą w stanie odtworzyć cokolwiek z tajemnicy. Co więcej, chcę, żeby wówczas odtworzyły już wszystko, bo mam nadzieję, że stanie się to jedynie na wypadek mojej śmierci.

Pozostaje pytanie: jak to zrobić? A może nawet właściwsze w tej sytuacji: czy to się w ogóle da zrobić? Okazuje się, że szczęśliwie się da. Zachęcam Ambitnych Czytelników do próby samodzielnego stworzenia takiego systemu.

A robi się to tak. Przedstawiam mój sekret w postaci ciągu zero-jedynkowego. Bitem będziemy nazywać dowolną cyfrę takiego ciągu, czyli zero lub jedynkę. Nietrudno zauważyć, że mogę znaleźć takie przedstawienie bez problemu, na przykład każdą literę alfabetu przedstawiam w postaci ciągu sześciu bitów, da się to zrobić, bo liter alfabetu jest nie więcej niż 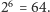Teraz mogę się więc skupić na tym, jak podzielić pewien ciąg bitów na trzy kawałki. Nie mogę po prostu przekazać pierwszej jednej trzeciej ABW, drugiej CIA, a trzeciej Mosadowi, bo w sposób oczywisty bez wysiłku każdy z nich znałby sporą część tajemnicy.

Żeby wyjaśnić system, konieczne jest zdefiniowanie funkcji 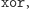która jako argumenty bierze pewną liczbę bitów, a zwraca jeden. Definiujemy ją jako

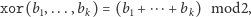
czyli resztę z dzielenia sumy bitów przez dwa. Możemy rozszerzyć funkcję 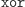w taki sposób, że jako argumenty bierze ona pewną liczbę ciągów bitowych jednakowej długości, powiedzmy dla ustalenia uwagi, długości 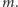Wtedy

gdzie przez oznaczamy 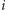-tą literę słowa Czyli, innymi słowy, nowy 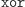po prostu xoruje argumenty litera po literze. Przykładowo

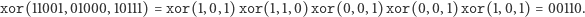
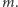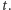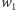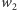A teraz system - jest banalnie prosty! Powiedzmy, że moja tajemnica przedstawiona w postaci ciągu bitów ma długość Jej wartość oznaczmy przez Najpierw losuję dwa losowe ciągi bitów i długości 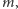to będą te przeznaczone dla ABW i CIA. Teraz definiuję trzeci ciąg, dla Mosadu, 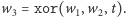Tylko dlaczego to działa?

Zauważmy najpierw, że 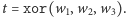Żeby się przekonać, że to prawda, spójrzmy na 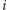-ty bit. Wiemy, że A więc suma oraz jest parzysta. Z tego zaś wynika, że Gdy powtórzymy rozumowanie dla każdego 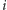między 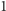a 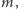otrzymamy, że faktycznie 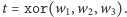Czyli ABW, CIA i Mosad współpracując, mogą odtworzyć moją tajemnicę.

Trzeba jednak jeszcze sprawdzić, czy istotnie żadne dwie służby bez trzeciej łącząc swoje siły, nie będą w stanie odkryć żadnej informacji. Jasne jest, że ABW i CIA mają ciągi losowe, więc nie zrobią z nimi niczego sensownego bez Mosadu. Pozostają pozostałe pary - skupmy się na parze CIA i Mosad, bo sytuacja jest identyczna dla pary ABW i Mosad. Przyjrzyjmy się 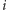-temu bitowi. Wyobraźmy sobie, że CIA i Mosad patrzą na swoje bity i widzą To im jednak nie daje żadnej wiedzy o bo może być tak, że oraz tak, że - każda z tych dwóch opcji jest równie prawdopodobna. Podobnie dla każdej kombinacji i oraz dla każdego innego indeksu 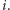Polecamy Czytelnikom Ambitnym doprecyzowanie tego argumentu.

Nietrudno zauważyć, że opisany system da się uogólnić na dowolne 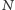służb. Jeszcze ciekawszym pytaniem jest, co zrobić, gdy chcę, by dowolne 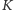z 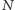służb, spotykając się, odtworzyło całą tajemnicę, ale już żadne 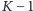służb nie mogło odkryć niczego. Wtedy potrzebne są bardziej zaawansowane techniki, pisaliśmy o tym w Delcie 2/2011.