Kocha, lubi, szyfruje...
W fizyce szkolnej nieustannie przewijającym się motywem są dwa znane miasta: miasto A oraz miasto B. W kryptografii takimi gwiazdami są Alicja i Bob, którzy ciągle się komunikują, uwierzytelniają, a zwykle przeszkadza im w tym złowroga Ewa.
Tym razem jednak zadanie stojące przed Alicją i Bobem jest wyjątkowo trudne. Chcą sprawdzić, czy się nawzajem kochają, jednak bez ujawniania swoich uczuć. Co przez to rozumiemy? Otóż chcemy opracować następujący protokół komunikacyjny.
Alicja posiada bit 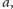 który informuje o tym, czy kocha Boba, czy nie (to oznacza, że
który informuje o tym, czy kocha Boba, czy nie (to oznacza, że 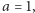 jeśli Alicja jest zakochana w Bobie, jeśli zaś nie jest, to
jeśli Alicja jest zakochana w Bobie, jeśli zaś nie jest, to 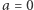 ). Analogicznie, Bob posiada bit
). Analogicznie, Bob posiada bit 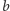 opisujący jego uczucia względem Alicji. Oczywiście teraz ich wzajemna miłość może być opisana w tej notacji przez wyrażenie
opisujący jego uczucia względem Alicji. Oczywiście teraz ich wzajemna miłość może być opisana w tej notacji przez wyrażenie 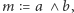 które jest równe
które jest równe  tylko wtedy, gdy
tylko wtedy, gdy 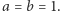 Naszym celem jest opracowanie takiego protokołu, w wyniku którego Alicja na końcu będzie znała
Naszym celem jest opracowanie takiego protokołu, w wyniku którego Alicja na końcu będzie znała  oraz
oraz 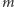 (i nic więcej!), natomiast Bob
(i nic więcej!), natomiast Bob 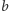 oraz
oraz 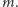 Intuicja stojąca za takimi założeniami jest następująca: chcemy uniknąć krępującej sytuacji, gdy, na przykład, Alicja kocha Boba, ale Bob nie odwzajemnia tych uczuć, a dowiaduje się o uczuciu Alicji. Innymi słowy: jeśli Bob wie, że
Intuicja stojąca za takimi założeniami jest następująca: chcemy uniknąć krępującej sytuacji, gdy, na przykład, Alicja kocha Boba, ale Bob nie odwzajemnia tych uczuć, a dowiaduje się o uczuciu Alicji. Innymi słowy: jeśli Bob wie, że 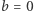 oraz
oraz 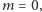 to nie powinien umieć wyznaczyć
to nie powinien umieć wyznaczyć 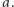
Powyższe założenia łatwo uzyskać, gdy dopuścimy trzecią zaufaną stronę, która, gdy pozna  i
i 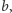 obliczy
obliczy 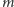 oraz przekaże tę informację obu zainteresowanym osobom. Nasze zadanie jest jednak bardziej ambitne, ponieważ pożądany efekt chcemy uzyskać za pomocą protokołu, w którym jedynymi stronami są Alicja i Bob. Zadanie samo w sobie wydaje się trudne, a wręcz można by przypuszczać, że tak określony protokół nie jest możliwy do zrealizowania. Pokażemy jednak, że jest to możliwe, ale przy pewnych założeniach obliczeniowych. Mamy tu na myśli klasyczne założenia dotyczące szyfrowania algorytmem RSA: a więc, że strona posiadająca jakąś wiadomość zaszyfrowaną oraz klucz publiczny bez znajomości klucza prywatnego nie jest w stanie odtworzyć wiadomości jawnej. Należy tu poczynić uwagę, że bez założeń tego typu (tj. bez ograniczeń obliczeniowych, inaczej mówiąc: bezpiecznie teorio-informacyjnie) żądanego protokołu nie da się skonstruować.
oraz przekaże tę informację obu zainteresowanym osobom. Nasze zadanie jest jednak bardziej ambitne, ponieważ pożądany efekt chcemy uzyskać za pomocą protokołu, w którym jedynymi stronami są Alicja i Bob. Zadanie samo w sobie wydaje się trudne, a wręcz można by przypuszczać, że tak określony protokół nie jest możliwy do zrealizowania. Pokażemy jednak, że jest to możliwe, ale przy pewnych założeniach obliczeniowych. Mamy tu na myśli klasyczne założenia dotyczące szyfrowania algorytmem RSA: a więc, że strona posiadająca jakąś wiadomość zaszyfrowaną oraz klucz publiczny bez znajomości klucza prywatnego nie jest w stanie odtworzyć wiadomości jawnej. Należy tu poczynić uwagę, że bez założeń tego typu (tj. bez ograniczeń obliczeniowych, inaczej mówiąc: bezpiecznie teorio-informacyjnie) żądanego protokołu nie da się skonstruować.
Wróćmy teraz do naszej Alicji i naszego Boba, którzy już za chwilę zaczną ze sobą rozmawiać.
Szukany protokół opiera się na idei tak zwanego transferu utajnionego (ang. oblivious transfer). Jest to bardzo ciekawy i użyteczny protokół, niejednokrotnie wykorzystywany jako cegiełka do budowy innych protokołów. Założenia są następujące: Alicja posiada parę liczb 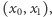 a Bob bit
a Bob bit 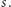 Po zakończeniu protokołu Alicja nie dowie się niczego nowego, natomiast Bob pozna liczbę
Po zakończeniu protokołu Alicja nie dowie się niczego nowego, natomiast Bob pozna liczbę 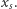 Taki protokół istnieje, pokażemy go później. Natomiast korzystając z transferu utajnionego, możemy już łatwo wykonać nasz docelowy protokół.
Taki protokół istnieje, pokażemy go później. Natomiast korzystając z transferu utajnionego, możemy już łatwo wykonać nasz docelowy protokół.
Niech mianowicie Alicja przyjmie:

a Bob:

W pierwszej fazie testu na miłość wykonujemy klasyczny transfer utajniony dla podanych parametrów. W jego wyniku Bob otrzymuje wartość 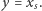 Wówczas wysyła ją Alicji i jest to wynik naszego protokołu.
Wówczas wysyła ją Alicji i jest to wynik naszego protokołu.
Łatwo sprawdzamy poprawność: jeśli 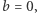 to wynikiem protokołu jest
to wynikiem protokołu jest 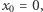 co jest zgodne z oczekiwaniami, gdyż
co jest zgodne z oczekiwaniami, gdyż

niezależnie od wartości 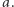 W drugim przypadku
W drugim przypadku 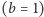 wynikiem jest
wynikiem jest 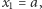 co również jest poprawną odpowiedzią, gdyż:
co również jest poprawną odpowiedzią, gdyż:

Transfer utajniony
W tej części pokażemy, jak zrealizować transfer utajniony. Jako narzędzia potrzebujemy szyfrowania z kluczem publicznym i prywatnym - dobrym przykładem jest tu wspomniany już algorytm RSA. Przypomnijmy założenia: Alicja posiada parę liczb 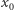 oraz
oraz 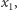 natomiast Bob ustala bit
natomiast Bob ustala bit 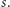 Teraz:
Teraz:
- 1.
- Alicja inicjalizuje algorytm RSA, tzn. wybiera liczbę
 oraz klucze
oraz klucze 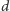 i
i 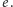 Zakładamy, że
Zakładamy, że 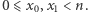 Swój klucz publiczny, czyli parę
Swój klucz publiczny, czyli parę 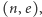 wysyła do Boba.
wysyła do Boba. - 2.
- Alicja losuje niezależnie dwie różne liczby
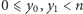 oraz wysyła je Bobowi.
oraz wysyła je Bobowi. - 3.
- Bob losuje liczbę
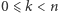 i oblicza
i oblicza 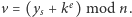 Bob wysyła wartość
Bob wysyła wartość  do Alicji.
do Alicji. - 4.
- Alicja oblicza kolejno:
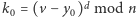 oraz
oraz 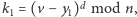
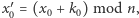
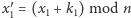 oraz wysyła Bobowi
oraz wysyła Bobowi 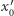 i
i 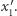
- 5.
- Bob potrafi obliczyć
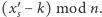
Sprawdźmy, że obliczona przez Boba wartość to rzeczywiście 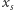 :
:

Aby opisany protokół był użyteczny, potrzebne są dwie własności:
- *
- Alicja nie poznaje bitu
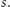 Ten fakt jest prosty - wynika z symetrii. To znaczy: z punktu widzenia Alicji nie ma w protokole żadnego rozróżnienia między
Ten fakt jest prosty - wynika z symetrii. To znaczy: z punktu widzenia Alicji nie ma w protokole żadnego rozróżnienia między 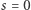 a
a 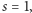 gdyż jedyny komunikat otrzymany od Boba (wartość
gdyż jedyny komunikat otrzymany od Boba (wartość  ) jest - z punktu widzenia Alicji - losowy i niezależny od wartości
) jest - z punktu widzenia Alicji - losowy i niezależny od wartości 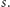
- **
- Bob nie poznaje liczby
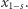
Pełny dowód (**) pominiemy i pozostawimy Czytelnikowi: wskazówka jest taka, że należy pokazać (metodą nie wprost), że gdyby można było złamać nasz protokół (a więc Bob dowiedziałby się czegoś na temat 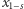 ), to złamać potrafilibyśmy również RSA. Rozumowania tego typu są bardzo częste w dowodach w kryptografii, czasem nazywamy je symulacją jednego protokołu przez drugi.
), to złamać potrafilibyśmy również RSA. Rozumowania tego typu są bardzo częste w dowodach w kryptografii, czasem nazywamy je symulacją jednego protokołu przez drugi.
Na sam koniec warto dodać, że opisany tutaj problem jest tylko drobnym przykładem na to, co potrafimy robić. Otóż okazuje się, że funkcja 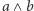 została wybrana zupełnie arbitralnie: tak naprawdę można podać protokół obliczający wartość dowolnej funkcji opisanej za pomocą obwodu logicznego. Wówczas ilość potrzebnej informacji, którą wymienią między sobą Alicja i Bob, jest proporcjonalna do liczby węzłów wspomnianego obwodu. Zainteresowanego Czytelnika zachęcamy do dalszych poszukiwań.
została wybrana zupełnie arbitralnie: tak naprawdę można podać protokół obliczający wartość dowolnej funkcji opisanej za pomocą obwodu logicznego. Wówczas ilość potrzebnej informacji, którą wymienią między sobą Alicja i Bob, jest proporcjonalna do liczby węzłów wspomnianego obwodu. Zainteresowanego Czytelnika zachęcamy do dalszych poszukiwań.
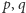 i oblicza
i oblicza 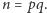 Następnie wyznacza liczbę
Następnie wyznacza liczbę  względnie pierwszą z
względnie pierwszą z 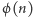 (czyli liczbą liczb względnie pierwszych z
(czyli liczbą liczb względnie pierwszych z 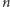 i mniejszych od
i mniejszych od 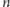 ) oraz jej odwrotność
) oraz jej odwrotność 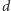 modulo
modulo 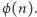 Jej kluczem publicznym jest para
Jej kluczem publicznym jest para 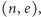 a kluczem prywatnym para
a kluczem prywatnym para 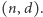 Szyfrowanie wiadomości
Szyfrowanie wiadomości 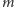 odbywa się według wzoru
odbywa się według wzoru 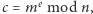 a odszyfrowywanie według wzoru
a odszyfrowywanie według wzoru