Nagrody Abela w roku 2020

Za co Hillel Furstenberg (Uniwersytet Hebrajski w Jerozolimie) oraz Gregory Margulis (Uniwersytet Yale w New Haven) otrzymali tegoroczną nagrodę?

Badania naukowe tegorocznych laureatów Nagrody Abela koncentrują się na głębokich zastosowaniach teorii ergodycznej w różnych zagadnieniach dotyczących teorii liczb, geometrii, aproksymacji czy kombinatoryki. Teoria ergodyczna, która jest częścią szerszej teorii układów dynamicznych, wyrosła około 100 lat temu z zagadnień czysto fizycznych. 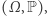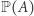W teorii tej zajmujemy się przestrzeniami probabilistycznymi $(Ω$ gdzie $|P(A)$ jest prawdopodobieństwem zdarzenia 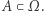$A$ Zazwyczaj 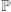$P$ jest określone tylko dla pewnej rodziny podzbiorów zbioru 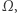$Ω$ zwanych zbiorami mierzalnymi. Na 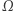$|Ω$ mamy dodatkowo określone przekształcenie 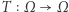$T Ω$ zachowujące prawdopodobieństwo 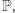$P,$ tzn. 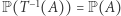$P(T −1(A))$ dla podzbiorów mierzalnych 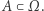$|A$ Przekształcenie 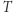$|T$ mówi nam, jak przebiega ewolucja punktów 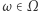$|ω$ w czasie:

ω

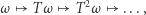zachowywanie prawdopodobieństwa zaś to pewne "prawo fizyczne" - ewolucja w naszym układzie dynamicznym 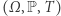$(Ω$ odbywa się z zachowaniem "objętości", tzn. z zachowaniem prawdopodobieństwa 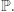$|P.$ Popatrzmy na bardzo prosty przykład układu dynamicznego. Niech 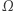$|Ω$ będzie okręgiem jednostkowym, tzn. 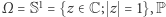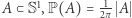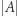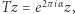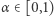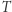niech $Ω$ zaś prawdopodobieństwem wyznaczonym przez żądanie, aby dla każdego łuku $|A$ (gdzie przez $A$ oznaczyliśmy długość łuku) i niech $2π iα |Tz = e z,$ gdzie $α ∈ [0,1)$ ( $|T$ jest obrotem o kąt 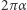$2π α$ ). Ten przykład jest charakterystyczny dla sytuacji, w której mamy dodatkową strukturę przestrzeni 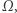$Ω$ tzn. mamy zadane "dobre" przekształcenie 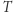$|T$ "dobrej" przestrzeni 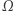$Ω$ i próbujemy opisać wszystkie możliwe prawdopodobieństwa niezmiennicze (w przykładzie powyżej można pokazać, że wskazane przez nas prawdopodobieństwo jest jedynym prawdopodobieństwem niezmienniczym, gdy $|α$ jest liczbą niewymierną). Natomiast sama teoria ergodyczna bada rozmieszczenie ( "geometrię") orbit punktów w przestrzeni, tzn. 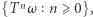zbiorów $n {T ω ,$ interesuje się własnościami "mieszającymi" (co jest wstępem do badania chaosu w układzie). Możemy np. 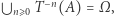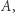pytać, czy $| nE0T−n(A) ,$ a dokładniej - pytać, czy z prawdopodobieństwem 1 orbita punktu $ω$ trafi do ustalonego zbioru $A,$ takiego że 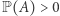$P(A) |$ (mówimy wtedy, że 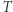$T$ jest przekształceniem ergodycznym). 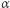W powyższym przykładzie przekształcenie $|T$ jest ergodyczne wtedy i tylko wtedy, gdy $α$ jest liczbą niewymierną. Możemy sprawdzać warunek mieszania dla podzbiorów mierzalnych $|A,$ :

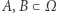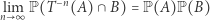lim P(T −n(A) n ∞

(a więc intuicyjnie zbiór 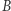$|B$ po pewnym czasie rozmazuje się po całej przestrzeni, przy czym jest on w każdym zbiorze 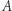$A$ proporcjonalnie do swojej miary). Ergodyczność i mieszanie to przykłady własności, które dla pewnych układów zachodzą, a dla innych nie zachodzą. Ale są też własności (dodajmy nieoczywiste), które zachodzą w każdym układzie dynamicznym. Dla przykładu w każdym układzie dynamicznym 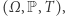$( |Ω$ dla dowolnego zbioru mierzalnego 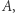$A,$ prawie każdy punkt 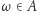$|ω$ powróci do zbioru $A$ nieskończenie wiele razy (ten fakt, zwany twierdzeniem o powracaniu, został odkryty przez Poincarégo jeszcze w XIX wieku). Znacznie głębsze jest słynne twierdzenie ergodyczne Birkhoffa (sprzed 90 lat), które mówi nam, że typowe punkty (tzn. 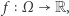punkty z pewnego zbioru o prawdopodobieństwie 1) "chodzą" po przestrzeni regularnie w tym sensie, że jeśli weźmiemy jakikolwiek "pomiar" na naszej przestrzeni (wyrażany przez funkcję $f | Ω$ powiedzmy "mierzalną" i ograniczoną), to średnie 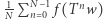$−1 |1N-PNn 0 f(T nw)$ mają granicę, gdy 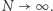$∞. N |$ A gdy układ 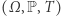$|(Ω$ jest dodatkowo ergodyczny, to granica ta będzie równa "średniej" funkcji 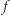$| f$ po całej przestrzeni (tzn. otrzymamy całkę funkcji $f$ względem prawdopodobieństwa $|P$ ).

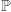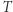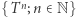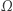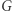Powyżej mówiliśmy o sytuacji, w której mamy do czynienia z jednym przekształceniem $T$ (choć właściwie rozpatrujemy zbiór $|{Tn;n ∈ N}$ ), ale można sobie wyobrażać, że na $|Ω$ działa rodzina przekształceń $},{T ;g ∈G g$ gdzie $G$ ma jakąś dodatkową strukturę. Dla przykładu możemy myśleć, że 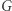$G$ jest pewną rodziną macierzy o wyznaczniku różnym od zera, zamkniętą ze względu na mnożenie i branie elementu odwrotnego - jest to więc szczególny przypadek struktury, którą w matematyce nazywa się grupą. 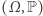Wtedy rodzina $} {T ;g ∈ G g$ jest pewną reprezentacją grupy $|G$ w zbiorze układów dynamicznych przestrzeni $(Ω$ (zakładamy zachowywanie struktur, tzn. zakładamy, że $|Tgh = Tg ○Th$ dla $g, h∈ G$ ). 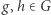I znowu możemy zadawać różne ciekawe pytania ergodyczne, których próbkę widzieliśmy powyżej, gdy "czas" $G$ był równy $|N.$ Czy taka abstrakcyjna teoria, która przecież musiała wypracować trudne metody, aby dowodzić w miarę ogólnych twierdzeń, może mieć cokolwiek wspólnego z bardziej "przyziemnymi" problemami matematyki? Okazuje się, że tak. Geniusz Hillela Furstenberga polegał m.in. na tym, że zaproponował on już w latach 70. XX wieku dalsze rozwijanie teorii ergodycznej w duchu twierdzeń dotyczących wielokrotnego powracania czy też zbieżności niekonwencjonalnych średnich ergodycznych. Widział on, że - może nieco wbrew swoim "fizycznym" korzeniom - twierdzenia teorii ergodycznej dają się interpretować jako twierdzenia o kombinatorycznych własnościach podzbiorów zbioru "czasów", w szczególności podzbiorów zbioru liczb naturalnych. 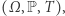Furstenberg udowodnił na przykład, że dla dowolnego układu dynamicznego $(Ω$ dowolnej liczby naturalnej 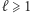$|ℓ⩾ 1$ i dowolnego zbioru 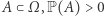$|A$ mamy

P(A

(*)

dla nieskończenie wielu 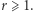$|r⩾ 1.$ Udowodnił on również, że powyższe twierdzenie jest równoważne pewnemu twierdzeniu opisującemu kombinatoryczne własności "dużych" podzbiorów liczb naturalnych. Zanim jednak przedstawimy jego pełne sformułowanie, potrzebujemy następującej definicji:

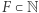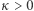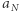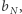Definicja 1 (górnej dodatniej gęstości Banacha). Powiemy, że zbiór $F ⊂ N$ ma własność GGBD, jeśli istnieje stała $κ > 0$ oraz dwa ciągi liczbowe $|aN$ i $bN ,$ które mają (dla każdego naturalnego 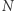$N$ ) następujące własności: 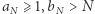$|a ⩾1,b > N N N$ i $-1 F ∩ [a ,a + b ] ⩾ κ. bN N N N$

A oto i samo twierdzenie:

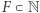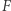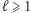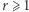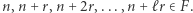
Twierdzenie. Jeśli $F ⊂ N$ ma własność GGBD, to zbiór $F$ zawiera postępy arytmetyczne dowolnej długości. Tzn. dla dowolnej liczby naturalnej $|ℓ⩾ 1$ istnieje takie $|r⩾ 1$ oraz $|n⩾ 1,$ że $|n,n +r,n + 2r,...,n+ ℓr ∈F.$

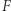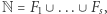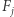W pewnym sensie widać, że zbiór $|F$ nie może być "dowolny", jakaś struktura całego zbioru liczb naturalnych w nim pozostała. Można spostrzec, że gdy $N = F1 ∪...∪ Fs,$ gdzie zbiory $|F j, j = 1,...,s$ są parami rozłączne, to któryś z tych zbiorów musi mieć własność GGBD, a więc w którymś ze zbiorów $Fj$ musiała "przeżyć" struktura zbioru 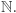$|N.$ Może jeszcze tytułem ciekawostki dodajmy, że aby udowodnić powyższe twierdzenie, udowodnione wcześniej przez matematyka węgierskiego Endre Szemerédiego (laureata Nagrody Abela w roku 2012) metodami czysto kombinatorycznymi, w (??) potrzebujemy "jedynie", żeby przekroje 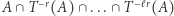$A$ były niepuste. Tak to już jednak bywa, że aby wykazać niepustość zbioru, tzn. istnienie "dobrej" konfiguracji bez wskazywania konkretnej konfiguracji, trzeba rozwinąć ogromną teorię wskazującą na powód niepustości.

Gdy chcemy dowodzić bardziej specyficznych własności teorioliczbowych czy też kombinatorycznych, często możemy zawęzić klasę układów dynamicznych, których pewne własności ergodyczne (o ile uda nam się je udowodnić) mają ciekawe i może bardziej intuicyjne implikacje. Niezwykle owocną rolę odgrywają tu tzw. układy dynamiczne pochodzenia algebraicznego, które są określone na pewnych strukturach ilorazowych grup macierzowych, a reprezentacja grupy 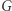$G$ pochodzi od "obrotów" wyznaczonych przez mnożenie macierzy (obroty niewymierne są tu bardzo prostym, bo jednowymiarowym, przykładem takich działań). Zilustrujmy to podejście słynną hipotezą Oppenheima o formach kwadratowych sprzed 90 lat, której prawdziwość udowodnił Gregory Margulis (laureat medalu Fieldsa z 1978 roku). 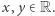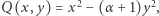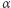Tytułem wprowadzenia popatrzmy na przypadek form zależących od dwóch zmiennych $x, y∈ R.$ Otóż można spostrzec, że wzór $|Q(x,$ gdzie $α$ jest złotą proporcją, tzn. 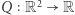$1 √ -- α = 2 ( 5 + 1)$ definiuje funkcję $|Q$ o następujących własnościach: (i) 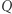$|Q$ jest formą kwadratową, (ii) 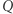$Q |$ przyjmuje zarówno wartości dodatnie, jak i ujemne ( 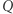$Q|$ nie jest ani dodatnio ani ujemnie określona), a ponadto (iii) 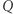$|Q$ nie jest proporcjonalna do formy o współczynnikach wymiernych. Jeśli teraz $x, | y ≠0$ są liczbami całkowitymi, to (wobec $|α2 = α + 1$ )

Q(x,

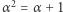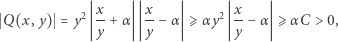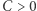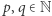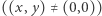gdyż złota liczba jest źle aproksymowalna liczbami wymiernymi: $| α − pq ⩾ C/q2$ dla pewnej stałej $C |$ i dowolnych $p,q ∈N$ ! Zatem wartości formy $| Q$ przyjmowane na argumentach całkowitych $| ((x, y)≠ (0,0))$ są odgraniczone od zera. Słynna hipoteza Oppenheima stanowiła, że jeśli użyjemy więcej zmiennych niż dwie, np. rozpatrując 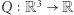$Q$ spełniające własności (i)-(iii) podane powyżej, to takiego odgraniczenia od zera nie możemy uzyskać. Jakie tutaj układy dynamiczne będą odpowiadały za rozwiązanie problemu? Dowód Margulisa polegał na studiowaniu orbit grupy przekształceń zachowujących formę i klasyfikacji miar niezmienniczych, które możemy uzyskać na domknięciu orbit w tzw. przestrzeni jednorodnej odpowiedniej grupy macierzy o wyznaczniku 1.

Wybitne osiągnięcia tegorocznych laureatów nagrody Abela (i ich uczniów) pokazują, jak nowe, często zaskakujące, idee prowadzą do przełomowych odkryć stanowiących o postępie w nauce.