Czy można wyobrazić sobie inną metodę uzyskiwania dostępu do skrzynki pocztowej? Taką, by nie trzeba było podawać hasła? W końcu stanowi to pewne zagrożenie dla naszego bezpieczeństwa: jeśli ktoś przechwyci, w ten czy inny sposób, nasze hasło i nazwę użytkownika, to uzyska nieograniczony dostęp do naszych zasobów – listów, dokumentów, historii przejrzanych stron – czego zapewne sobie nie życzymy.

Dowody z wiedzą zerową

Z pomocą przychodzą wtedy tzw. dowody z wiedzą zerową. Są to protokoły pozwalające na potwierdzenie faktu znajomości pewnej informacji bez ujawniania jej. Dla lepszego zilustrowania tego typu protokołów rozpatrzmy następujący przykład weryfikacji tożsamości w banku:

Przykład 1

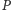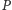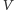W protokole tym będzie brało udział dwóch „graczy” – pierwszy będzie chciał potwierdzić swoją tożsamość i oznaczany będzie literą  (od angielskiego słowa Prover; gracz ten jest nazywany także klientem), drugi będzie weryfikował informacje przesyłane przez gracza  i oznaczany będzie literą  (od angielskiego słowa Verifier; inna nazwa tego gracza to weryfikator).

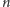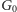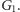W protokole wykorzystywane są dwa grafy o  wierzchołkach,  i  Gracz 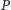 będzie starał się udowodnić, że są one izomorficzne. Należy tu nadmienić, że stwierdzenie, czy dane dwa grafy są izomorficzne, jest w ogólnym przypadku problemem trudnym obliczeniowo i nie jest znane jego rozwiązanie działające w czasie wielomianowym.

Ale jaki związek ma dowodzenie izomorficzności grafów z uwierzytelnianiem? Możemy przyjąć, że w bazie danych banku znajduje się informacja z imieniem i nazwiskiem gracza 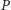 oraz grafam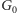i  i 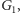 znanymi publicznie, podanymi przez gracza 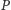 podczas zakładania konta. Gracz 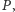 chcąc przekonać bank, że on to on, przedstawia się, a następnie wykazuje, że jest osobą, która potrafi udowodnić izomorficzność grafów 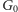 i 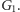 Mógłby to, oczywiście, zrobić, zdradzając permutację 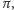 jednak po takim zabiegu nic nie stałoby na przeszkodzie, by nieuczciwy gracz 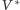 po poznaniu permutacji podszył się pod klienta 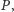 wypłacając w jego imieniu dużą ilość gotówki. 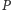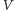Zamiast tego gracze  i  przeprowadzą między sobą 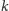 razy następujący protokół (oznaczmy go jako ):

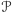(1)

Klient 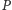 wybiera losową permutację 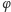 zbioru 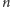 -elementowego i przesyła do weryfikatora 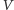 graf

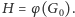
(2)

Weryfikator 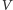 przysyła graczowi 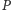 losowy bit

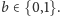
(3)

Jeśli otrzymany przez gracza 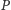 bit ma wartość 0, to wybiera on nową permutację 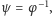 a w przeciwnym przypadku 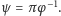 Gracz 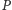 wysyła następnie permutację 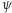 do weryfikatora

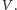
(4)

Weryfikator 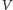 sprawdza teraz, czy 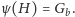 Jeśli tak, to uznaje, że gracz 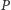 pomyślnie przeszedł proces weryfikacji. Jeśli nie, odrzuca jego próbę i przerywa protokół.

Od takiego protokołu będziemy wymagać trzech rzeczy. Po pierwsze, protokół przeprowadzony przez uczciwego gracza 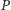 musi zostać zaakceptowany. Po drugie, próba udowodnienia nieprawdziwego twierdzenia (w tym przypadku – próba wykazania, że dwa nieizomorficzne grafy są izomorficzne) powinna powodować zatrzymanie i brak akceptacji protokołu (z prawdopodobieństwem bliskim 1). Podobnie będzie z próbą udowodnienia prawdziwego twierdzenia przy braku znajomości przez gracza permutacji wyznaczającej izomorfizm. Trzecią własnością jest wiedza zerowa, tj. weryfikator 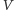 po wykonaniu (nawet wielokrotnym) protokołu 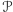 nie może podszyć się pod gracza

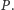
Na początku wykażemy, że jeśli klient 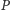 jest uczciwy, to weryfikator 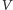 zaakceptuje jego próbę uwierzytelnienia się. Otóż jeżeli bit wysłany przez weryfikatora 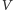 w drugim kroku protokołu miał wartość 0, to uczciwy klient 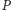 odpowiedział na niego permutacją 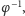 co daje 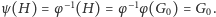 Załóżmy teraz, że przesłany bit miał wartość 1. Klient 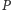 wysyła wtedy permutację 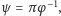 więc 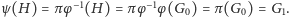 Zatem w obu przypadkach 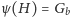 i weryfikator 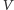 akceptuje wykonanie protokołu.

Wykażemy teraz, dlaczego protokół 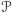 zostanie przerwany przez weryfikatora 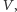 jeśli oszust 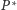 będzie próbował przekonać go do nieprawdziwego twierdzenia. Przyjmijmy więc, że klient 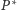 został pozytywnie zweryfikowany przez 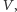 podczas gdy grafy 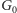 i 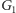 nie są izomorficzne. Załóżmy, że w każdym z 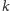 wykonań protokołu oszust umiał odpowiedzieć poprawnie, zarówno wtedy, gdy zadany w drugim kroku bit miał wartość 0, jak i 1. 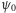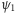Niech  i  oznaczają funkcje 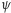 otrzymane w trzecim kroku algorytmu, gdy zadany przez weryfikatora 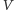 bit miał odpowiednio wartość 0 i 1. 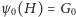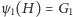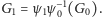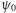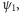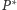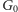Mamy wtedy  i  oraz  Czyli, znając  i  oszust  jest w stanie wskazać izomorfizm pomiędzy grafami  i 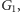 co nie jest możliwe. Mogło oczywiście być tak, że w każdym z 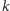 wykonań protokołu gracz 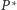 poprawnie zgadł wartość bitu, o jaki zostanie zapytany przez sprawdzającego 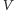 (łatwo wykazać, że stworzenie takiego grafu 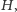 iż oszust 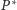 jest w stanie poprawnie odpowiedzieć na dokładnie jedną wartość bitu 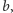 nie stanowi problemu, jednak wtedy szansa na powodzenie tej iteracji protokołu wynosi dokładnie 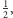 gdyż takie jest prawdopodobieństwo, że weryfikator 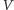 wylosuje bit 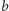 o ustalonej wartości). Jednak to zdarzenie ma prawdopodobieństwo równe 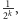 a więc dla odpowiednio dużego 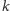 jest zaniedbywalnie małe.

Powyższe rozumowanie wykazuje również, iż nieuczciwy gracz 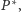 który próbuje przekonać weryfikatora 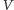 do tego, że zna permutację 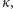 taką że 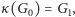 mimo braku tej wiedzy, też nie zakończy protokołu sukcesem (tj. zaakceptowaniem przez weryfikatora ).

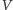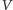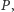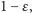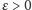Aby wykazać, że weryfikator  w podanym protokole nie dowiaduje się niczego istotnego o sekrecie gracza  tj. mimo wielokrotnego przeprowadzenia protokołu nie jest w stanie podszyć się pod niego, wprowadza się pojęcie symulatora działającego w czasie wielomianowym (z prawdopodobieństwem równym  gdzie  jest zaniedbywalnie małe). Symulator 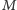 wykonuje protokół z weryfikatorem 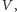„podszywając się” pod 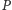 (  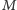nie ma dostępu do prywatnych informacji gracza 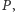 a jedynie zna jego odpowiedzi na pewną liczbę zapytań w procesie weryfikacji). 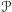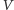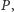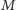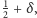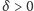Protokół  jest bezpieczny, gdy weryfikator  nie jest w stanie stwierdzić, czy operacje, które wykonuje, przeprowadza z prawdziwym graczem  czy z symulatorem  (prawdopodobieństwo, że odpowie dobrze, jest równe  gdzie  jest zaniedbywalnie małe). Formalny opis symulatora 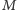 i przeprowadzenie pełnego rozumowania wymaga

wprowadzenia dużej ilości nowej terminologii i zostanie w tym artykule pominięte. Zainteresowani Czytelnicy są zachęcani do przeczytania literatury podanej na końcu artykułu.

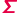-protokoły

Zaprezentowany powyżej protokół musiał być wykonywany wiele razy pod rząd, by można go było użyć do weryfikacji, ponieważ poprawne „przejście” jego pojedynczej iteracji przez nieuprawnionego gracza ma szansę powodzenia

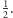
Aby ograniczyć liczbę iteracji do minimum (czytaj: do jednej), wprowadzono protokoły, w których gracz weryfikujący 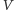 przesyła w drugim kroku zamiast pojedynczego bitu 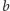 ciąg 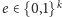 zwany wyzwaniem, który traktujemy jako liczbę naturalną zapisaną binarnie. Ilustracją tej metody może być protokół zaprezentowany poniżej:

Przykład 2

Niech 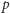 i 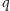 będą liczbami pierwszymi, takimi że 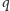 jest dzielnikiem  i niech 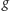 będzie elementem rzędu 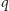 w grupie 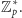 Ponadto niech 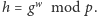 W zaprezentowanym protokole wartośc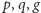i  i 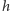 są publiczne, a gracz 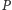 będzie przekonywać gracza 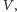 że zna wartość 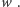 Zrobi to w następujący sposób:

(1)

Gracz 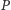 wybiera losowo liczbę  z ciała 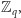 a następnie wysyła graczowi 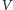 liczbę

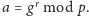
(2)

Weryfikator 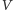 wybiera losowe wyzwanie 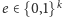 i wysyła je graczowi

(3)

Gracz 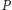 oblicza 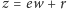 i wysyła tę wartość weryfikatorowi.

(4)

Weryfikator sprawdza, czy 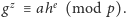 Jeśli tak, akceptuje protokół, a jeśli nie, przerywa go.

Przede wszystkim zauważmy, że uczciwy gracz 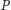 zostanie zawsze zaakceptowany przez gracza 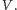 Jak łatwo sprawdzić, 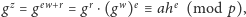 co jest zgodne z ostatnim punktem protokołu.

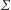 -protokoły mają jeszcze jedną interesującą własność: jeśli gracz 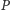 potrafi przy danym 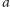 odpowiedzieć na dwa różne wyzwania  i 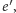 to potrafi znaleźć świadka 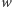 (a zatem odpowiedzieć na dowolne wyzwanie). Przyjmując, że odpowiedzią gracza 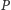 na wyzwanie  było 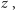 a odpowiedzią na wyzwanie 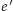 było 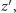 mamy:

Dzieląc jedno równanie przez drugie i mając na uwadze fakt, że 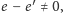 otrzymamy

W ten sposób uzyskaliśmy 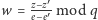 (dzielenie rozumiemy tutaj jako mnożenie przez odwrotność modulo 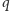). Zatem jeśli gracz 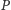 nie zna sekretu 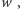 to jest w stanie odpowiedzieć poprawnie na co najwyżej jedno wyzwanie weryfikatora 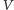 (na jakie wyzwanie konkretnie będzie chciał odpowiadać, wybiera, tworząc wiadomość ). Prawdopodobieństwo, że gracz 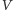 wyśle mu wybrane przez niego wyzwanie 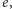 wynosi 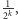 a więc jest zaniedbywalnie małe.

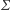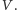Warto w tym miejscu zaznaczyć, że -protokoły nie mają wspomnianej wcześniej własności bycia protokołem z wiedzą zerową. Są nimi, jeśli przyjmiemy dodatkowe założenie – o uczciwości weryfikatora  Wydaje się, że jest ono niezbyt praktyczne, ale własność ta jest wystarczająca do budowy wielu bardziej złożonych konstrukcji, które mają zastosowanie w realnym świecie. Na przykład, można dzięki nim zbudować efektywny system obsługi płatności elektronicznych, który zapewnia taką samą anonimowość jak płacenie gotówką. Ale to już całkiem inna historia...