Bardzo oszczędne drzewa (II)
Skoro dotychczas szło nam tak dobrze, spróbujmy pójść za ciosem i zaproponować bardzo oszczędną reprezentację drzew już niekoniecznie binarnych (ale wciąż ukorzenionych)...
Skoro dotychczas szło nam tak dobrze, spróbujmy pójść za ciosem i zaproponować bardzo oszczędną reprezentację drzew już niekoniecznie binarnych (ale wciąż ukorzenionych)...
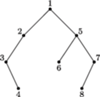
Rys. 1
Wiele struktur danych w komputerze można reprezentować w postaci drzewa binarnego. Aby przechować takie drzewo w pamięci komputera, należy dla każdego węzła zapamiętać numer jego lewego i prawego syna oraz, jeśli to potrzebne, numer węzła będącego jego ojcem. Wystarczą nam do tego trzy tablice.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku omówimy dwa zadania z Potyczek Algorytmicznych 2012. Pomimo krótkich rozwiązań, zadania te wymagały od zawodników niemałej dozy pomysłowości.
Algorytmy Informatyczny kącik olimpijski
Tym razem w kąciku zadanie Świetliki, z którym mierzyli się finaliści Potyczek Algorytmicznych 2013.
Algorytm to sposób rozwiązania pewnego problemu. Informatyka i matematyka od dawna badają różnego rodzaju problemy, szukając dla nich algorytmów, najczęściej możliwie szybkich. My jednak tym razem postąpimy wręcz przeciwnie: zajmiemy się algorytmami wyjątkowo wolnymi.
Algorytmy Informatyczny kącik olimpijski
Tym razem omówimy zadanie o drogach stanowych (State Roads) z pierwszej rundy zawodów Yandex.Algorithm 2013. Zadanie to można sformułować w języku teorii grafów, a do tego w ujęciu dynamicznym...
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zmierzymy się z zadaniem Karty z Potyczek Algorytmicznych 2013. Oryginalne sformułowanie zadania dotyczyło kart perforowanych, my jednak przedstawimy je nieco inaczej, przy okazji wprowadzając niejawnie kilka nieznaczących uproszczeń.

Wipipedia
Zapewne każdy z nas dobrze zna muszkę owocówkę (drosophila melanogaster, co tłumaczy się dosłownie jako ciemnobrzucha miłośniczka rosy). Dla większości ta dobra znajomość niekoniecznie musi budzić dobre skojarzenia – być może z uwagi na jej natrętny muszy charakter i masową obecność letnią porą w pobliżu nieopatrznie zostawionych bez przykrycia słodkich owoców. Niemal równie powszechna jest wiedza o jej zasługach naukowych w dziedzinie genetyki. Mało kto zdaje sobie sprawę z tego, że to nie pies Łajka, a właśnie muszka była pierwszą ziemską istotą, która wybrała się w podróż kosmiczną. Ale czy ktoś uwierzy, że muszka pomogła również w rozwiązywaniu pewnego problemu z pogranicza matematyki i informatyki?
Ten numer Delty jest zdominowany przez tematykę skojarzeń w grafach. Dla
przypomnienia: graf nieskierowany to zbiór wierzchołków połączonych krawędziami,
skojarzenie zaś w tym grafie to taki podzbiór krawędzi
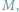 że każdy
wierzchołek grafu jest incydentny z co najwyżej jedną krawędzią z
że każdy
wierzchołek grafu jest incydentny z co najwyżej jedną krawędzią z
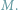
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Dwóch generałów, które pochodzi z Uniwersyteckich Zawodów Informatycznych organizowanych przez Uniwersytet Jagielloński, a konkretnie z konkursu z października 2009 roku.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Delayed search, które pojawiło się w 2004 r. w konkursie Internet Problem Solving Contest, organizowanym co roku przez Słowaków. Zadanie jest wariacją na temat znanej zabawy „zgadnij, o jakiej liczbie myślę”...
Algorytmy Informatyczny kącik olimpijski
W tym kąciku omówimy Dwa torty – kolejne zadanie z finałowej rundy Potyczek Algorytmicznych 2012.
Jedną z najczęściej wykonywanych operacji w geometrii obliczeniowej jest sortowanie
biegunowe (zwane też kątowym) zbioru
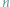 punktów na płaszczyźnie
względem wybranego punktu. Innymi słowy, chcemy uporządkować punkty
punktów na płaszczyźnie
względem wybranego punktu. Innymi słowy, chcemy uporządkować punkty
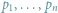 według współrzędnej kątowej w układzie biegunowym zaczepionym
w wybranym punkcie
według współrzędnej kątowej w układzie biegunowym zaczepionym
w wybranym punkcie
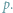 Stosując jeden z efektywnych algorytmów sortowania,
operację tę można zrealizować w czasie
Stosując jeden z efektywnych algorytmów sortowania,
operację tę można zrealizować w czasie
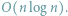
Czy programy liniowe mają coś wspólnego z informatyką? Okazuje się, że bardzo wiele. Po pierwsze, istnieją (bardzo ciekawe!) efektywne algorytmy rozwiązujące programy liniowe. Ponadto, programy liniowe są kluczowym narzędziem w optymalizacji kombinatorycznej, algorytmach aproksymacyjnych czy algorytmach online...
Algorytmy Informatyczny kącik olimpijski
Jednym z klasycznych problemów algorytmicznych jest tzw. problem plecakowy...
Kiedy rozwiązujemy jakiś problem informatyczny, często naszym celem jest podanie jak
najefektywniejszego algorytmu. Jednak czasem możemy natknąć się przy
tym na „ścianę” – danego problemu nie da się rozwiązać tak efektywnie, jak
byśmy tego chcieli. Najpowszechniej znanym przykładem opisanego zjawiska jest
klasa problemów NP-zupełnych. O problemach z tej klasy (a należy do niej
wiele naturalnych i praktycznych zagadnień) podejrzewa się, że nie da się ich
rozwiązać w czasie wielomianowym względem rozmiaru danych wejściowych.
Niestety, tylko podejrzewa się, a rozstrzygnięcie tej hipotezy (znanej też jako
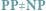 ?) jest obecnie najsłynniejszym otwartym problemem informatyki
teoretycznej.
?) jest obecnie najsłynniejszym otwartym problemem informatyki
teoretycznej.
Algorytmy Informatyczny kącik olimpijski
Tym razem zajmiemy się zadaniem z finałów Akademickich Mistrzostw Świata w Programowaniu Zespołowym 2012, które odbyły się w Warszawie. Zadanie zatytułowane Infiltration zostało rozwiązane przez 31 spośród 112 drużyn i było średnim pod względem trudności zadaniem na tych zawodach.
Na artykule Problemy 3sum-trudne w geometrii autor podał trzy wersje problemu PolygonContainment, które są uważane za trudne – nie umiemy ich rozwiązać w czasie (istotnie) lepszym niż kwadratowy. Uważni Czytelnicy na pewno zauważyli, że nie jest tam wspomniane o wersji, w której wielokąty są wypukłe i dopuszczamy dowolne przesunięcia (ale nie obroty). Ten brak jest w pełni uzasadniony, gdyż tę wersję problemu można rozwiązać w czasie liniowym względem liczby wierzchołków wielokątów, co pokażemy poniżej.
O zadaniu z Akademickich Mistrzostw Polski w Programowaniu Zespołowym (2012)
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Quadrilaterals z obozu w Petrozawodsku
w 2006 roku. Na płaszczyźnie dane jest
 punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
Dany jest graf nieskierowany
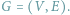 Kliką nazwiemy taki podzbiór
wierzchołków
Kliką nazwiemy taki podzbiór
wierzchołków
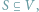 że każde dwa wierzchołki w zbiorze
że każde dwa wierzchołki w zbiorze
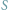 są
połączone krawędzią w grafie
są
połączone krawędzią w grafie
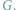 Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Algorytmy Informatyczny kącik olimpijski
Zadanie Odśnieżanie z zeszłorocznego Obozu Naukowo-Treningowego im. A. Kreczmara
można sformułować w języku teorii grafów następująco. W nieskierowanym,
ważonym, spójnym grafie
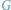 wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
Podziały liczb są ciekawymi obiektami kombinatorycznymi o dosyć skomplikowanych
własnościach. W tym artykule przedstawimy dwa algorytmy zliczania takich
obiektów. Pierwszy prosty algorytm będzie działał w czasie
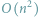 i pamięci
i pamięci
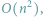 natomiast drugi, pochodzący od Eulera i oparty na tzw. liczbach
pentagonalnych, w czasie
natomiast drugi, pochodzący od Eulera i oparty na tzw. liczbach
pentagonalnych, w czasie
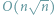 i pamięci
i pamięci
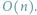
Algorytmy Informatyczny kącik olimpijski
W niedawno wydanej książce W poszukiwaniu wyzwań – zbiorze zadań
z konkursów programistycznych – Filip Wolski opisał rozwiązanie zadania Dwa
przyjęcia z finału XII Olimpiady Informatycznej. W zadaniu tym występuje
 osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...
osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...