Delta mi!

Jakiś czas temu koleżanki i koledzy z redakcji Delty poprosili mnie, żebym opisał, czym zajmuję się naukowo, i przedstawił pewien ciekawy wynik, który udało mi się wraz ze współpracownikami niedawno uzyskać. Pisząc ten tekst, postaram się przybliżyć tę właśnie dziedzinę, która mi osobiście wydaje się interesująca chyba dlatego, że rozważa problemy o bardzo prostym sformułowaniu geometrycznym, a mimo to jest w niej więcej znaków zapytania niż odpowiedzi. Badania często okazują się ciekawą kombinatoryką, popartą jednak zwykle geometrycznymi intuicjami. Wiele fundamentalnych pytań otwartych można sformułować bardzo szybko, jedno z nich przybliżę na końcu tego tekstu.

W informatyce wielokrotnie spotykamy się z sytuacjami, gdy tworzone algorytmy są w pewnym stopniu inspirowane przyrodą. Mamy na przykład algorytmy genetyczne, mrówkowe, rojowe czy symulowane wyżarzanie. Okazuje się, że obliczenia mogą być nie tylko inspirowane przez przyrodę, ale również przez przyrodę wykonywane!

W czasach niepewności, wielkich zmian, kryzysów ludzie więcej myślą o sprawach ostatecznych. Czy to nie zbliża się koniec cywilizacji, a może nawet całego świata? W dawnych czasach dobrym wzorem ładu i uporządkowania był Kosmos w dostatecznie dużej skali. No bo przecież nie Ziemia, ze swoją przyziemną nieprzewidywalnością - ale już jej wspólna podróż z Księżycem wokół Słońca, od "zawsze" taka sama, mogłaby stanowić jakiś punkt odniesienia. Albo jeszcze lepiej: popatrzmy na cały Układ Słoneczny! Czy jego leniwie przemierzające przestrzeń planety są oazą spokoju, przewidywalności i stabilności - jeśli nie na wieczność, to może przynajmniej na miliony, lub lepiej miliardy, lat?

W tym kąciku zajmiemy sią zadaniem z finału Potyczek Algorytmicznych 2009.

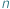Zaczniemy od takiego zadania: dla danego -literowego słowa chcemy znaleźć liczbę jego różnych podciągów. Innymi słowy, chcemy odpowiedzieć na pytanie, ile różnych słów możemy uzyskać poprzez wykreślanie niektórych liter ze słowa 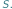Dla przykładu rozważmy słowo ABAA. Ma ono dokładnie 10 różnych podciągów: słowo puste, A, B, AA, AB, BA, AAA, ABA, BAA oraz ABAA. Dla uproszczenia będziemy rozważać słowa złożone z liter A i B, ale nasze rozwiązania będą działać dla dowolnego 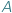-literowego alfabetu.

Tym razem omówimy zadanie Yet Another Substring Reverse, które pojawiło się na portalu www.codeforces.com.

Wiele zadań konkursowych proponowanych podczas zawodów programistycznych wymaga od uczestników zakodowania zawiłych algorytmów czy skomplikowanych struktur danych. Właśnie takie zadania nie raz i nie dwa, ale wielokrotnie prezentujemy w niniejszej rubryce. Dziś jednak opowiemy o pewnym bardzo specyficznym typie zadań olimpijskich, które zwykle sprowadzają się do znalezienia zwartego wzoru opisującego odpowiedź na pytanie zawarte w zadaniu...

Tym razem omówimy zadanie "Theater Tickets", które pojawiło się w konkursie Zinc 2018 organizowanym przez firmę Codility.

Korzystając z popularnych serwisów internetowych, błyskawicznie znajdziemy najkrótszą trasę między dwoma miastami. A co, gdybyśmy chcieli znaleźć najkrótszą trasę, która pozwoli po wyruszeniu z domu odwiedzić wszystkie interesujące nas miasta i wrócić do punktu wyjścia?

Tym razem omówimy zadanie "Beautiful Password", które pojawiło się na konkursie Cuprum 2018 organizowanym przez firmę Codility.

W tym odcinku omówimy rozwiązanie zadania "Cyfrowy ciąg", które pojawiło się w eliminacjach do zawodów Romanian Master of Informatics.

Podczas odbywającego się w 1900 roku w Paryżu Drugiego Międzynarodowego Kongresu Matematyków jeden z referatów wygłosił wybitny niemiecki matematyk David Hilbert. W swoim wystąpieniu zawarł on listę dwudziestu trzech zagadnień matematycznych stanowiących, jego zdaniem, szczególne wyzwanie dla matematyków w rozpoczynającym się XX wieku. Większość z nich doczekała się rozwiązania. Inne, jak słynna hipoteza Riemanna, pozostają otwarte, inspirując kolejne pokolenia naukowców.

W tym odcinku omówimy rozwiązanie zadania XORanges, które pojawiło się na trzecich zawodach European Junior Olympiad in Informatics (Maribor, Słowenia).

W tym odcinku omówimy rozwiązanie zadania "123-Pairs", które pojawiło się na "Code Festival 2016".

Czy pokazując poprawność algorytmu, warto sięgnąć po matematyczne twierdzenia? Jak najbardziej! Przekonamy się o tym, rozważając problem zbalansowanego rozwoju w 2-wymiarowych systemach dodawania wektorów ( Vector Addition Systems - VAS), ubrany w historyjkę o zawodniku i trenerze.

W tym odcinku omówimy rozwiązanie zadania "Kwadraty liczb naturalnych", które pojawiło się na finale Zawodów Indywidualnych XIII Młodzieżowej Olimpiady Informatycznej.

W tym odcinku omówimy rozwiązanie zadania "Telekomunikacja", które pojawiło się na drugim etapie Zawodów Drużynowych XIII Młodzieżowej Olimpiady Informatycznej.

W tym odcinku omówimy rozwiązanie zadania "Trzej znajomi", które pojawiło się na drugim etapie XIII Młodzieżowej Olimpiady Informatycznej.

W tym odcinku omówimy rozwiązanie zadania "Domino", które pojawiło się w 2018 roku w ramach X International Autumn Tournament in Informatics w Szumen, w Bułgarii.

W tym odcinku omówimy rozwiązania dwóch zadań z pierwszego etapu XIII Młodzieżowej Olimpiady Informatycznej.

Jak mierzyć trudność problemów? Trudność albo, inaczej mówiąc, ich skomplikowanie, złożoność. To nie jest łatwe pytanie. Aby móc na nie chociaż nieco sensownie odpowiedzieć, skupimy się tu na tzw. problemach decyzyjnych, czyli takich, na które odpowiedź zawsze brzmi "tak" lub "nie". Żeby określić, jak złożone są te problemy, przyjmuje się zasadę, że problem jest tak trudny, jak jego najlepsze rozwiązanie. Innymi słowy mówimy, że złożoność problemu jest równa złożoności najlepszego algorytmu, który go rozwiązuje.

Tym razem omówimy zadanie Liczby prawie pół-pierwsze, które pojawiło się na Sobotnim Kole Naukowym (25.11.2017) organizowanym przez Stowarzyszenie Talent w III Liceum Ogólnokształcącym w Gdyni.

Tym razem omówimy dwa zadania: Wyspę z IX OIG oraz Liczydło z XII OIG.