Podróże w 
Jakiś czas temu koleżanki i koledzy z redakcji Delty poprosili mnie, żebym opisał, czym zajmuję się naukowo, i przedstawił pewien ciekawy wynik, który udało mi się wraz ze współpracownikami niedawno uzyskać. Pisząc ten tekst, postaram się przybliżyć tę właśnie dziedzinę, która mi osobiście wydaje się interesująca chyba dlatego, że rozważa problemy o bardzo prostym sformułowaniu geometrycznym, a mimo to jest w niej więcej znaków zapytania niż odpowiedzi. Badania często okazują się ciekawą kombinatoryką, popartą jednak zwykle geometrycznymi intuicjami. Wiele fundamentalnych pytań otwartych można sformułować bardzo szybko, jedno z nich przybliżę na końcu tego tekstu.
Niedawno w Delcie 7/2020 pisałem o podróżach w 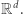 Można też równoważnie powiedzieć, że były to podróże w
Można też równoważnie powiedzieć, że były to podróże w 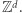 Jedną z konsekwencji omawianego tam lematu Steinitza był fakt mówiący, że jeśli układ
Jedną z konsekwencji omawianego tam lematu Steinitza był fakt mówiący, że jeśli układ  równań liniowych o
równań liniowych o  zmiennych i wartościach bezwzględnych wszystkich współczynników występujących w równaniach ograniczonych przez
zmiennych i wartościach bezwzględnych wszystkich współczynników występujących w równaniach ograniczonych przez  ma rozwiązanie, to ma rozwiązanie niewielkie. Konkretnie rzecz biorąc, ma takie rozwiązanie
ma rozwiązanie, to ma rozwiązanie niewielkie. Konkretnie rzecz biorąc, ma takie rozwiązanie  że jego norma (tzn. maksimum z wartości bezwzględnych współrzędnych) jest ograniczona przez
że jego norma (tzn. maksimum z wartości bezwzględnych współrzędnych) jest ograniczona przez 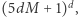 nie zależy w ogóle od liczby równań
nie zależy w ogóle od liczby równań 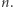 Ten fakt z kolei implikuje, że pytania o podróże w
Ten fakt z kolei implikuje, że pytania o podróże w  stają się stosunkowo łatwe. Rozważmy następujący problem osiągalności w
stają się stosunkowo łatwe. Rozważmy następujący problem osiągalności w 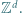 Dany jest zbiór wektorów
Dany jest zbiór wektorów 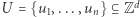 oraz wektory początkowy
oraz wektory początkowy  i końcowy
i końcowy 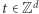 takie, że normy wszystkich
takie, że normy wszystkich  oraz
oraz  są ograniczone przez
są ograniczone przez 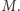 Pytamy, czy istnieje taka podróż składająca się z przystanków w punktach
Pytamy, czy istnieje taka podróż składająca się z przystanków w punktach 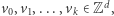 że zaczyna się ona w
że zaczyna się ona w  (czyli
(czyli 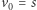 ), kończy w
), kończy w 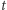 (czyli
(czyli 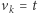 ), a każdy krok jest przesunięciem o któryś wektor
), a każdy krok jest przesunięciem o któryś wektor 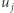 (czyli dla każdego
(czyli dla każdego 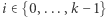 istnieje
istnieje 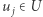 taki, że
taki, że 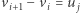 ). Jak łatwo zauważyć, jest to równoważne pytaniu, czy istnieją współczynniki
). Jak łatwo zauważyć, jest to równoważne pytaniu, czy istnieją współczynniki 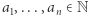 (określające, ile razy użyjemy w trakcie podróży każdego z wektorów), takie że
(określające, ile razy użyjemy w trakcie podróży każdego z wektorów), takie że 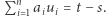 Z faktu powyżej wynika, że jeśli istnieje podróż z
Z faktu powyżej wynika, że jeśli istnieje podróż z  do
do 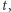 to istnieje taka podróż długości co najwyżej
to istnieje taka podróż długości co najwyżej 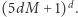 To w szczególności powoduje, że problem osiągalności w
To w szczególności powoduje, że problem osiągalności w 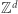 należy do klasy NP, możemy zgadnąć współczynniki
należy do klasy NP, możemy zgadnąć współczynniki 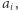 które są reprezentowane przez liczby o wielomianowo wielu bitach, i sprawdzić, że rzeczywiście spełniają równość
które są reprezentowane przez liczby o wielomianowo wielu bitach, i sprawdzić, że rzeczywiście spełniają równość 
Dziś rozważymy problem osiągalności w 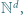 bardzo podobny do problemu osiągalności w
bardzo podobny do problemu osiągalności w 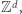 a jednak, jak się okaże, o zupełnie innych własnościach. Podobnie jak poprzednio w problemie osiągalności w
a jednak, jak się okaże, o zupełnie innych własnościach. Podobnie jak poprzednio w problemie osiągalności w 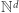 dany jest zbiór wektorów
dany jest zbiór wektorów 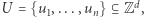 wektor początkowy
wektor początkowy  i końcowy
i końcowy 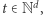 każdy z nich o normie ograniczonej przez
każdy z nich o normie ograniczonej przez 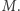 Również pytamy o istnienie takiej podróży
Również pytamy o istnienie takiej podróży 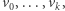 że
że 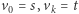 oraz każdy krok
oraz każdy krok 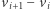 jest równy pewnemu wektorowi
jest równy pewnemu wektorowi 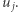 Wymagamy jednak, żeby każdy punkt podróży
Wymagamy jednak, żeby każdy punkt podróży 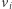 miał wszystkie współrzędne nieujemne, czyli
miał wszystkie współrzędne nieujemne, czyli  Innymi słowy, cała nasza podróż ma się zmieścić w dodatniej ćwiartce układu współrzędnych (dla
Innymi słowy, cała nasza podróż ma się zmieścić w dodatniej ćwiartce układu współrzędnych (dla 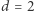 ), a ogólnie w dodatnim ortancie
), a ogólnie w dodatnim ortancie  Okazuje się, że problem osiągalności w
Okazuje się, że problem osiągalności w  jest dużo trudniejszy od swojego odpowiednika w
jest dużo trudniejszy od swojego odpowiednika w 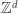 i wciąż daleki od matematycznego zrozumienia.
i wciąż daleki od matematycznego zrozumienia.
Bardzo często rozważa się pewne eleganckie uogólnienie problemu osiągalności w 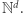 Dodajemy do naszych rozważań stany, intuicyjnie rzecz biorąc, oznacza to, że w każdym punkcie naszej podróży jesteśmy w jednym ze skończenie wielu trybów, zwanych stanami. Opis problemu składa się wtedy również z podania skończonego zbioru stanów
Dodajemy do naszych rozważań stany, intuicyjnie rzecz biorąc, oznacza to, że w każdym punkcie naszej podróży jesteśmy w jednym ze skończenie wielu trybów, zwanych stanami. Opis problemu składa się wtedy również z podania skończonego zbioru stanów 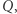 a każdy krok podróży określany jest nie tylko wektorem z
a każdy krok podróży określany jest nie tylko wektorem z 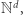 a raczej trójką
a raczej trójką 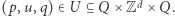 Taka trójka
Taka trójka 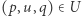 oznacza, że jeśli jestem w stanie
oznacza, że jeśli jestem w stanie 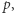 to mogę przesunąć się o wektor
to mogę przesunąć się o wektor  i zmienić stan na
i zmienić stan na 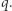 Wprowadzenie stanów tylko pozornie komplikuje sprawę. System z wektorami w
Wprowadzenie stanów tylko pozornie komplikuje sprawę. System z wektorami w 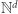 i
i  stanami można stosunkowo łatwo zasymulować systemem o wektorach z
stanami można stosunkowo łatwo zasymulować systemem o wektorach z 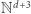 i bez stanów. Dodajemy do systemu trzy współrzędne i wtedy konfigurację: stan
i bez stanów. Dodajemy do systemu trzy współrzędne i wtedy konfigurację: stan 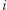 -ty, wektor
-ty, wektor 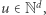 reprezentujemy jako wektor
reprezentujemy jako wektor 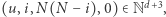 który na pierwszych
który na pierwszych 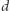 współrzędnych ma wektor
współrzędnych ma wektor  Przy odrobinie sprytu jesteśmy w stanie zakodować również ruchy w systemie ze stanami w tych
Przy odrobinie sprytu jesteśmy w stanie zakodować również ruchy w systemie ze stanami w tych 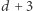 współrzędnych (przy czym jednemu ruchowi w oryginalnym systemie odpowiadać będzie pewien ciąg ruchów w jego reprezentacji). Ostatnia współrzędna nie jest używana przy kodowaniu stanów, ale przydaje się przy implementacji ruchów. Dociekliwy Czytelnik może spróbować dopowiedzieć sobie szczegóły.
współrzędnych (przy czym jednemu ruchowi w oryginalnym systemie odpowiadać będzie pewien ciąg ruchów w jego reprezentacji). Ostatnia współrzędna nie jest używana przy kodowaniu stanów, ale przydaje się przy implementacji ruchów. Dociekliwy Czytelnik może spróbować dopowiedzieć sobie szczegóły.

Rys. 1
Żeby poczuć nieco, jak ciekawe własności mogą mieć takie systemy, rozważmy przykład pokazany na rysunku 1 System ten ma dwa stany: 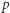 i
i 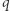 oraz cztery możliwe ruchy oznaczone strzałkami i ich etykietami. Przyjrzyjmy się, jaką podróż możemy wykonać, startując ze stanu
oraz cztery możliwe ruchy oznaczone strzałkami i ich etykietami. Przyjrzyjmy się, jaką podróż możemy wykonać, startując ze stanu  i punktu
i punktu 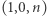 ; będziemy oznaczali taką konfigurację
; będziemy oznaczali taką konfigurację 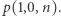
Na początek możemy wykonać następującą trasę:
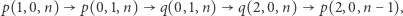 |
i jesteśmy z powrotem w stanie 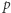 z trzecim licznikiem o jeden mniejszym, ale za to pierwszym dwa razy większym. Możemy wykonać analogiczną trasę ponownie
z trzecim licznikiem o jeden mniejszym, ale za to pierwszym dwa razy większym. Możemy wykonać analogiczną trasę ponownie

gdzie przez 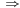 oznaczamy kilka ruchów pod rząd. Powtarzając tę procedurę, możemy dotrzeć do konfiguracji
oznaczamy kilka ruchów pod rząd. Powtarzając tę procedurę, możemy dotrzeć do konfiguracji 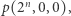 a stąd bardzo prosto do dowolnej konfiguracji postaci
a stąd bardzo prosto do dowolnej konfiguracji postaci  gdzie
gdzie  Nietrudno zauważyć, że konfiguracji, do których można dojść z
Nietrudno zauważyć, że konfiguracji, do których można dojść z  jest skończenie wiele, a konkretnie rzecz biorąc, wykładniczo wiele względem
jest skończenie wiele, a konkretnie rzecz biorąc, wykładniczo wiele względem 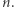 Ciekawym pytaniem (choć nie otwartym) jest, jak duży może być zbiór konfiguracji osiągalnych z jednej ustalonej konfiguracji w przypadku, gdy jest on skończony. Zachęcam Czytelników do konstrukcji systemu, w którym taki zbiór jest podwójnie wykładniczy względem wielkości początkowej konfiguracji oraz wielkości systemu (w szczególności liczb na strzałkach). Przy pewnym wysiłku można skonstruować system, który ma ten zbiór konfiguracji wielkości rzędu wieży dwójek wysokości
Ciekawym pytaniem (choć nie otwartym) jest, jak duży może być zbiór konfiguracji osiągalnych z jednej ustalonej konfiguracji w przypadku, gdy jest on skończony. Zachęcam Czytelników do konstrukcji systemu, w którym taki zbiór jest podwójnie wykładniczy względem wielkości początkowej konfiguracji oraz wielkości systemu (w szczególności liczb na strzałkach). Przy pewnym wysiłku można skonstruować system, który ma ten zbiór konfiguracji wielkości rzędu wieży dwójek wysokości 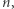 czyli
czyli  a nawet dużo większy (rzędu
a nawet dużo większy (rzędu  funkcje
funkcje 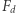 omówię poniżej).
omówię poniżej).
Problem osiągalności w 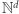 jest badany w informatyce teoretycznej od lat 70. XX wieku. Znany jest w delikatnie się różniących, ale równoważnych wersjach, pod nazwą problemu osiągalności w sieciach Petriego bądź problemu osiągalności w systemach zwanych Vector Addition Systems (brak tu powszechnie używanej polskiej nazwy). Warto podkreślić, dlaczego ten problem jest w ogóle rozważany w informatyce teoretycznej. Mianowicie sieci Petriego są jednym z podstawowych modeli programów współbieżnych, a zostały wprowadzone w latach 30. przez Carla Petriego w kontekście modelowania reakcji chemicznych. Gdy mamy w pewnym systemie
jest badany w informatyce teoretycznej od lat 70. XX wieku. Znany jest w delikatnie się różniących, ale równoważnych wersjach, pod nazwą problemu osiągalności w sieciach Petriego bądź problemu osiągalności w systemach zwanych Vector Addition Systems (brak tu powszechnie używanej polskiej nazwy). Warto podkreślić, dlaczego ten problem jest w ogóle rozważany w informatyce teoretycznej. Mianowicie sieci Petriego są jednym z podstawowych modeli programów współbieżnych, a zostały wprowadzone w latach 30. przez Carla Petriego w kontekście modelowania reakcji chemicznych. Gdy mamy w pewnym systemie  różnych substancji chemicznych, to określając liczbę ich cząsteczek liczbami naturalnymi, możemy opisać sytuację wektorem w
różnych substancji chemicznych, to określając liczbę ich cząsteczek liczbami naturalnymi, możemy opisać sytuację wektorem w 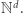 W takiej sytuacji reakcja chemiczna, która rozkłada 3 cząsteczki pierwszej substancji na 2 cząsteczki drugiej substancji i 4 cząsteczki trzeciej substancji, a czwartej substancji w ogóle nie dotyczy, może być przedstawiona jako zmiana o wektor
W takiej sytuacji reakcja chemiczna, która rozkłada 3 cząsteczki pierwszej substancji na 2 cząsteczki drugiej substancji i 4 cząsteczki trzeciej substancji, a czwartej substancji w ogóle nie dotyczy, może być przedstawiona jako zmiana o wektor 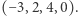 Podobnie możemy modelować inne systemy, w których równocześnie istnieje wiele zasobów. Mogą to być towary dostępne na giełdzie lub liczby procesów odpowiedniego typu w danym programie. Problem osiągalności odpowiada więc na pytanie, czy zaczynając z danego układu, można po pewnej liczbie modyfikacji dojść do pewnego innego układu. To pytanie jest przydatne przy automatycznej weryfikacji programów komputerowych: możemy zapytać, czy zaczynając z konfiguracji początkowej, można po pewnej liczbie kroków otrzymać określoną konfigurację błędną. Ta obserwacja jest jednym w ważnych powodów zainteresowania informatyki teoretycznej sieciami Petriego i ich problemem osiągalności. Ma jednak duże znaczenie również fakt, że problem osiągalności w
Podobnie możemy modelować inne systemy, w których równocześnie istnieje wiele zasobów. Mogą to być towary dostępne na giełdzie lub liczby procesów odpowiedniego typu w danym programie. Problem osiągalności odpowiada więc na pytanie, czy zaczynając z danego układu, można po pewnej liczbie modyfikacji dojść do pewnego innego układu. To pytanie jest przydatne przy automatycznej weryfikacji programów komputerowych: możemy zapytać, czy zaczynając z konfiguracji początkowej, można po pewnej liczbie kroków otrzymać określoną konfigurację błędną. Ta obserwacja jest jednym w ważnych powodów zainteresowania informatyki teoretycznej sieciami Petriego i ich problemem osiągalności. Ma jednak duże znaczenie również fakt, że problem osiągalności w 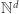 jest też po prostu bardzo naturalnym zagadnieniem geometrycznym.
jest też po prostu bardzo naturalnym zagadnieniem geometrycznym.
Co zaskakujące, przez dłuższy czas nie było wiadomo, czy w ogóle istnieje jakikolwiek algorytm rozwiązujący problem osiągalności w 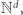 innymi słowy, czy problem ten jest rozstrzygalny. Pierwszy algorytm został zaproponowany przez Ernsta Mayra w roku 1978, po około dziesięciu latach badań. Nie było jednak znane żadne ograniczenie na złożoność obliczeniową tego problemu. Inaczej mówiąc, wiadomo było, że algorytm działa bardzo wolno, ale nawet trudno powiedzieć, jak wolno. Pomimo wielu lat badań nad podobnymi problemami najlepszy aktualnie znany algorytm, opublikowany w 2019 roku przez Leroux i Schmitza, działa w czasie rzędu
innymi słowy, czy problem ten jest rozstrzygalny. Pierwszy algorytm został zaproponowany przez Ernsta Mayra w roku 1978, po około dziesięciu latach badań. Nie było jednak znane żadne ograniczenie na złożoność obliczeniową tego problemu. Inaczej mówiąc, wiadomo było, że algorytm działa bardzo wolno, ale nawet trudno powiedzieć, jak wolno. Pomimo wielu lat badań nad podobnymi problemami najlepszy aktualnie znany algorytm, opublikowany w 2019 roku przez Leroux i Schmitza, działa w czasie rzędu 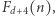 gdzie
gdzie  to rozmiar danych wejściowych, a
to rozmiar danych wejściowych, a  to wymiar przestrzeni
to wymiar przestrzeni  Funkcje
Funkcje 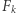 to przykład bardzo szybko rosnących funkcji, zdefiniowanych (w jednej z wersji definicji) następująco:
to przykład bardzo szybko rosnących funkcji, zdefiniowanych (w jednej z wersji definicji) następująco: 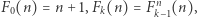 czyli
czyli 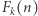 to
to 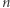 -krotne złożenie funkcji
-krotne złożenie funkcji 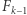 na argumencie
na argumencie 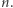 Mamy wówczas
Mamy wówczas

gdzie w  wieża dwójek jest wysokości
wieża dwójek jest wysokości 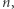 a liczba
a liczba  i następne są już dość trudne do wyobrażenia. Widać więc, że faktycznie najlepszy znany dziś algorytm dla problemu osiągalności jest bardzo wolny.
i następne są już dość trudne do wyobrażenia. Widać więc, że faktycznie najlepszy znany dziś algorytm dla problemu osiągalności jest bardzo wolny.
To nie znaczy jednak, że każdy algorytm musi być tak wolny. Znane są pewne dolne ograniczenia na złożoność problemu, ale jest tu wiele znaków zapytania. Już w roku 1976 Richard Lipton udowodnił, że problem osiągalności w 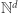 jest
jest  -trudny, czyli z grubsza rzecz biorąc, że żaden algorytm nie może działać szybciej niż w pamięci wykładniczej. W szczególności nie może działać w czasie szybszym niż podwójnie wykładniczy. Jednak przez wiele lat dość powszechną hipotezą było, że taki algorytm działający w czasie podwójnie wykładniczym powinien istnieć. Wielu osobom wydawało się prawdopodobne, że jeśli istnieje podróż od konfiguracji startowej
-trudny, czyli z grubsza rzecz biorąc, że żaden algorytm nie może działać szybciej niż w pamięci wykładniczej. W szczególności nie może działać w czasie szybszym niż podwójnie wykładniczy. Jednak przez wiele lat dość powszechną hipotezą było, że taki algorytm działający w czasie podwójnie wykładniczym powinien istnieć. Wielu osobom wydawało się prawdopodobne, że jeśli istnieje podróż od konfiguracji startowej  do końcowej
do końcowej  to istnieje również taka podróż o długości co najwyżej podwójnie wykładniczej. Osobiście, z tego, co pamiętam, też wierzyłem w tę hipotezę. Konkretnie rzecz biorąc, wspomniana konstrukcja Liptona pokazuje, że podróże w
to istnieje również taka podróż o długości co najwyżej podwójnie wykładniczej. Osobiście, z tego, co pamiętam, też wierzyłem w tę hipotezę. Konkretnie rzecz biorąc, wspomniana konstrukcja Liptona pokazuje, że podróże w 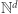 nie mogą być krótsze niż rzędu
nie mogą być krótsze niż rzędu  co dla stałego
co dla stałego  oraz
oraz 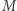 reprezentowanego binarnie jest ograniczeniem wykładniczym. Dopiero w 2018 roku udało się nam z kolegami udowodnić, że problem osiągalności w
reprezentowanego binarnie jest ograniczeniem wykładniczym. Dopiero w 2018 roku udało się nam z kolegami udowodnić, że problem osiągalności w 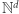 nie może dać się rozwiązać szybciej niż w czasie
nie może dać się rozwiązać szybciej niż w czasie 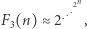 co w szczególności implikuje, że istnieją systemy, w których najkrótsza ścieżka jest bardzo długa, np. długości ośmiokrotnie wykładniczej. Temu dowodowi można przyjrzeć się w artykule na serwisie arXiv: arxiv.org/abs/1809.07115. Przedstawię tu jednak pewien przykład, który pokazuje, że oszacowanie Liptona nie jest optymalne. Ten przykład był jednym z początkowych na naszej drodze do ostatecznego rozwiązania i naprowadził nas na właściwą konstrukcję. Sam w sobie zaś stanowi ciekawe zrozumienie tego, co może stać się w wymiarze
co w szczególności implikuje, że istnieją systemy, w których najkrótsza ścieżka jest bardzo długa, np. długości ośmiokrotnie wykładniczej. Temu dowodowi można przyjrzeć się w artykule na serwisie arXiv: arxiv.org/abs/1809.07115. Przedstawię tu jednak pewien przykład, który pokazuje, że oszacowanie Liptona nie jest optymalne. Ten przykład był jednym z początkowych na naszej drodze do ostatecznego rozwiązania i naprowadził nas na właściwą konstrukcję. Sam w sobie zaś stanowi ciekawe zrozumienie tego, co może stać się w wymiarze 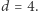
Tak jak wspomniałem powyżej, konstrukcja Liptona pokazywała, że w stałym wymiarze 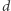 najkrótsze podróże mogą być długości rzędu
najkrótsze podróże mogą być długości rzędu 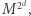 czyli wykładnicze, ale nieznane były przykłady, w których są one istotnie dłuższe. Przykład, który udało nam się znaleźć, pokazuje, że już w stosunkowo niewielkim wymiarze najkrótsze podróże mogą być długości podwójnie wykładniczej. Konstrukcja opiera się na następującym lemacie, dotyczącym ułamków, co dość zaskakująco okazuje się związane z podróżami w
czyli wykładnicze, ale nieznane były przykłady, w których są one istotnie dłuższe. Przykład, który udało nam się znaleźć, pokazuje, że już w stosunkowo niewielkim wymiarze najkrótsze podróże mogą być długości podwójnie wykładniczej. Konstrukcja opiera się na następującym lemacie, dotyczącym ułamków, co dość zaskakująco okazuje się związane z podróżami w 
Lemat. Dla każdego 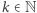 istnieje
istnieje  ułamków
ułamków  takich że
takich że

 oraz
oraz  są ograniczone przez
są ograniczone przez 
Zauważmy, że istnienie ułamków postulowanych w lemacie wcale nie jest oczywiste. Żeby 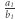 był nie większy niż
był nie większy niż 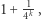 to jego mianownik musi być równy co najmniej
to jego mianownik musi być równy co najmniej  Taki ułamek podniesiony do potęgi
Taki ułamek podniesiony do potęgi 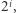 dla
dla  rzędu
rzędu 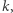 ma licznik oraz mianownik podwójnie wykładniczy względem
ma licznik oraz mianownik podwójnie wykładniczy względem 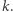 Trudność w dowodzie powyższego lematu polega na tym, że liczniki i mianowniki wielu ułamków podwójnie wykładniczej wielkości muszą się poskracać przy mnożeniu w taki sposób, by w rezultacie otrzymany został ułamek
Trudność w dowodzie powyższego lematu polega na tym, że liczniki i mianowniki wielu ułamków podwójnie wykładniczej wielkości muszą się poskracać przy mnożeniu w taki sposób, by w rezultacie otrzymany został ułamek 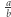 dla
dla  i
i  wielkości wykładniczej względem
wielkości wykładniczej względem 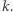 Dowodu lematu nie przedstawimy, choć dałoby się go udowodnić mniej więcej na jednej stronie.
Dowodu lematu nie przedstawimy, choć dałoby się go udowodnić mniej więcej na jednej stronie.
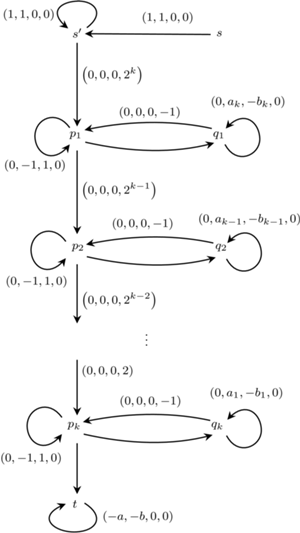
Rys. 2
Teraz pokażemy bardzo szkicowo, w jaki sposób lemat może posłużyć do konstrukcji zbioru ruchów dla 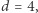
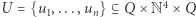 oraz konfiguracji
oraz konfiguracji
takich 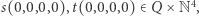 że podróż z
że podróż z  do
do 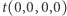 przy użyciu
przy użyciu 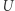 jest podwójnie wykładnicza względem wielkości tych wektorów. System jest zilustrowany na rysunku 2 (niepodpisane ruchy oznaczają brak przesunięcia). Tak dobraliśmy zbiór
jest podwójnie wykładnicza względem wielkości tych wektorów. System jest zilustrowany na rysunku 2 (niepodpisane ruchy oznaczają brak przesunięcia). Tak dobraliśmy zbiór 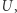 żeby każda podróż musiała wyglądać w bardzo konkretny sposób. Na początku generujemy wektor postaci
żeby każda podróż musiała wyglądać w bardzo konkretny sposób. Na początku generujemy wektor postaci 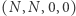 przy użyciu pętli w stanie o efekcie
przy użyciu pętli w stanie o efekcie 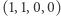 w stanie
w stanie 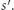 Potem mnożymy drugą współrzędną przez
Potem mnożymy drugą współrzędną przez  w stanach
w stanach 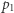 i
i 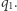 Robimy to podobnie, jak w systemie na rysunku 1, używając dwóch stanów. Tam mnożyliśmy liczbę 1 przez ułamek
Robimy to podobnie, jak w systemie na rysunku 1, używając dwóch stanów. Tam mnożyliśmy liczbę 1 przez ułamek 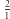 co najwyżej
co najwyżej  razy, ale każde mnożenie mogło mieć pewne straty. W efekcie po
razy, ale każde mnożenie mogło mieć pewne straty. W efekcie po 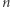 pętlach między stanami
pętlach między stanami 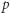 i
i  z liczby 1 uzyskaliśmy najwyżej liczbę
z liczby 1 uzyskaliśmy najwyżej liczbę 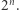 W analogiczny sposób możemy pomnożyć liczbę
W analogiczny sposób możemy pomnożyć liczbę 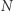 przez co najwyżej
przez co najwyżej 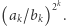 Następnie mamy
Następnie mamy 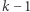 podobnych faz, w których mnożymy drugą współrzędną przez co najwyżej
podobnych faz, w których mnożymy drugą współrzędną przez co najwyżej 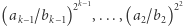 i na końcu przez co najwyżej
i na końcu przez co najwyżej 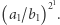 Po tych wszystkich operacjach nasza druga współrzędna ma wartość co najwyżej
Po tych wszystkich operacjach nasza druga współrzędna ma wartość co najwyżej 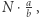 co wynika z równania w lemacie. A więc cała konfiguracja ma postać
co wynika z równania w lemacie. A więc cała konfiguracja ma postać 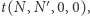 gdzie
gdzie 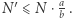 Na koniec w stanie
Na koniec w stanie 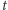 w pętli odejmujemy wektor
w pętli odejmujemy wektor 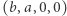 i chcemy dojść do konfiguracji
i chcemy dojść do konfiguracji 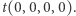 Okazuje się, że jedyny sposób dojścia do
Okazuje się, że jedyny sposób dojścia do 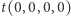 jest taki, żeby
jest taki, żeby 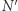 było równe dokładnie
było równe dokładnie 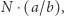 a to z kolei jest możliwe tylko, jeśli wszystkie mnożenia na trasie były dokładne. Pierwsze mnożenie, to w stanach
a to z kolei jest możliwe tylko, jeśli wszystkie mnożenia na trasie były dokładne. Pierwsze mnożenie, to w stanach 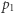 i
i 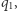 było mnożeniem przez
było mnożeniem przez 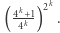 Aby było zrealizowane dokładnie, to liczba
Aby było zrealizowane dokładnie, to liczba 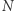 musiała być podzielna przez
musiała być podzielna przez 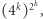 co jest liczbą podwójnie wykładniczą, a więc oznacza, że
co jest liczbą podwójnie wykładniczą, a więc oznacza, że  musiało być podwójnie wykładnicze. Zatem oczywiście długość trasy też musiała być podwójnie wykładnicza, co kończy szkic konstrukcji. Szczegóły można znaleźć w artykule w serwisie arXiv: arxiv.org/abs/2001.04327.
musiało być podwójnie wykładnicze. Zatem oczywiście długość trasy też musiała być podwójnie wykładnicza, co kończy szkic konstrukcji. Szczegóły można znaleźć w artykule w serwisie arXiv: arxiv.org/abs/2001.04327.
Przedstawiona konstrukcja dowodzi, że istnieją systemy w wymiarze 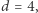 które mają najkrótszą ścieżkę pomiędzy dwoma niewielkimi konfiguracjami długości podwójnie wykładniczej względem opisu systemu. Czy możemy skonstruować takie systemy z najkrótszą ścieżką potrójnie wykładniczą? Tego nie wiadomo. Najlepsze górne oszacowanie to
które mają najkrótszą ścieżkę pomiędzy dwoma niewielkimi konfiguracjami długości podwójnie wykładniczej względem opisu systemu. Czy możemy skonstruować takie systemy z najkrótszą ścieżką potrójnie wykładniczą? Tego nie wiadomo. Najlepsze górne oszacowanie to 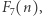 czyli olbrzymie. Co ciekawe, podobnie jest również dla innych wymiarów. Dla
czyli olbrzymie. Co ciekawe, podobnie jest również dla innych wymiarów. Dla 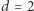 wiadomo, że w każdym systemie o ile dany punkt jest osiągalny w
wiadomo, że w każdym systemie o ile dany punkt jest osiągalny w 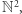 to jest osiągalny trasą co najwyżej wykładniczej długości. Wiadomo też, że są systemy, w których taka trasa wykładniczej długości jest faktycznie najkrótszą trasą. Jak jednak wygląda sytuacja dla wymiaru
to jest osiągalny trasą co najwyżej wykładniczej długości. Wiadomo też, że są systemy, w których taka trasa wykładniczej długości jest faktycznie najkrótszą trasą. Jak jednak wygląda sytuacja dla wymiaru 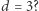 Tego również nie wiadomo. Najlepsze znane górne oszacowanie to funkcja
Tego również nie wiadomo. Najlepsze znane górne oszacowanie to funkcja 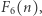 czyli dużo większa niż wieża dwójek wysokości
czyli dużo większa niż wieża dwójek wysokości 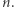 Możliwe jest też, że zawsze taka najkrótsza trasa jest wykładniczej długości. Osobiście obstawiam, że druga możliwość jest prawdziwa, ale to tylko dywagacje. Być może odpowiedzi udzieli ktoś z Czytelników, tworząc konstrukcję podobną do powyższej. Rozwiązania problemów otwartych od dziesięcioleci wcale nie muszą być bardzo trudne.
Możliwe jest też, że zawsze taka najkrótsza trasa jest wykładniczej długości. Osobiście obstawiam, że druga możliwość jest prawdziwa, ale to tylko dywagacje. Być może odpowiedzi udzieli ktoś z Czytelników, tworząc konstrukcję podobną do powyższej. Rozwiązania problemów otwartych od dziesięcioleci wcale nie muszą być bardzo trudne.