Informatyczny kącik olimpijski
Po prostu znajdź wzór
Wiele zadań konkursowych proponowanych podczas zawodów programistycznych wymaga od uczestników zakodowania zawiłych algorytmów czy skomplikowanych struktur danych. Właśnie takie zadania nie raz i nie dwa, ale wielokrotnie prezentujemy w niniejszej rubryce. Dziś jednak opowiemy o pewnym bardzo specyficznym typie zadań olimpijskich, które zwykle sprowadzają się do znalezienia zwartego wzoru opisującego odpowiedź na pytanie zawarte w zadaniu...
Jako przykład niech posłuży nam zadanie "Count the Arrays", prezentowane na platformie Codeforces. Zadanie jest następujące:
Zadanie. Na wejściu otrzymujemy dwie liczby naturalne  oraz
oraz 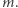 Interesować nas będą pewne bardzo specyficzne ciągi. Konkretnie powiemy, że ciąg jest elegancki, jeśli zawiera
Interesować nas będą pewne bardzo specyficzne ciągi. Konkretnie powiemy, że ciąg jest elegancki, jeśli zawiera  elementów o wartościach w zbiorze
elementów o wartościach w zbiorze 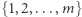 oraz:
oraz:
- (*)
- istnieje dokładnie jedna para elementów ciągu, które są sobie równe;
- (**)
- istnieje indeks
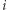 (szczytowy) taki, że ciąg jest ściśle rosnący na pozycjach
(szczytowy) taki, że ciąg jest ściśle rosnący na pozycjach 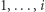 oraz ściśle malejący na pozycjach
oraz ściśle malejący na pozycjach 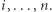
Niech teraz 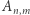 oznacza liczbę eleganckich ciągów dla pewnych ustalonych
oznacza liczbę eleganckich ciągów dla pewnych ustalonych 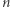 i
i 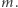 Celem zadania jest obliczenie
Celem zadania jest obliczenie 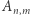 (modulo 998244353).
(modulo 998244353).
Rozwiązanie. Twierdzimy, że prawdziwy jest wzór:
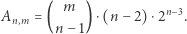 |
Dlaczego? Aby go udowodnić, spróbujmy zdefiniować "procedurę" generowania wszystkich rozważanych 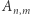 ciągów. Otóż wyobraźmy sobie, iż w pierwszym kroku chcemy zadecydować, które w ogóle elementy choć raz pojawią się w naszym ciągu. Ponieważ ciąg ma długość
ciągów. Otóż wyobraźmy sobie, iż w pierwszym kroku chcemy zadecydować, które w ogóle elementy choć raz pojawią się w naszym ciągu. Ponieważ ciąg ma długość 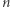 i tylko jeden element się powtarza - co więcej zawsze z krotnością 2 - to widać, że różnych elementów jest zawsze
i tylko jeden element się powtarza - co więcej zawsze z krotnością 2 - to widać, że różnych elementów jest zawsze 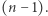 Możemy więc je wybrać ze zbioru wartości na dokładnie
Możemy więc je wybrać ze zbioru wartości na dokładnie 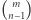 sposobów. Zauważmy, że gdy już ustalimy swój "alfabet", to element szczytowy został już wybrany. Tam, gdzie mamy jeszcze swobodę, to wybór elementu zduplikowanego - dokonujemy go na
sposobów. Zauważmy, że gdy już ustalimy swój "alfabet", to element szczytowy został już wybrany. Tam, gdzie mamy jeszcze swobodę, to wybór elementu zduplikowanego - dokonujemy go na 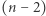 sposobów (możemy wybrać każdy, poza szczytowym). Dla wszystkich pozostałych
sposobów (możemy wybrać każdy, poza szczytowym). Dla wszystkich pozostałych 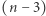 (poza szczytowym i zduplikowanymi) elementów musimy jeszcze podjąć decyzję, czy dany element znajdzie się po lewej, czy po prawej stronie szczytu. Różnych możliwości jest więc
(poza szczytowym i zduplikowanymi) elementów musimy jeszcze podjąć decyzję, czy dany element znajdzie się po lewej, czy po prawej stronie szczytu. Różnych możliwości jest więc 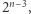 a ustalenie tego wyboru już determinuje cały ciąg - elementy z obu stron szczytu są posortowane, więc nie pozostała już żadna swoboda w generowaniu eleganckich ciągów. Ta obserwacja kończy dowód prawdziwości postulowanego wzoru.
a ustalenie tego wyboru już determinuje cały ciąg - elementy z obu stron szczytu są posortowane, więc nie pozostała już żadna swoboda w generowaniu eleganckich ciągów. Ta obserwacja kończy dowód prawdziwości postulowanego wzoru.
Zadania takie jak wyżej mogą oczywiście sprawiać kłopot w trakcie analizy kombinatorycznej, ale gdy już znajdziemy stosowny wzór, to wydaje się, że wystarczy już tylko napisać króciutki programik, który oblicza i zwraca wynik. W zasadzie jest to prawda, ale i tu czyhają pułapki. Skupimy się na dwóch problemach:
1. Jak szybko obliczyć 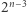 (modulo 998244353)?
(modulo 998244353)?
Kolejne potęgowanie dwójki może okazać się za wolne dla dużych wartości 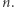 Wówczas warto skorzystać z metody, która działa w czasie
Wówczas warto skorzystać z metody, która działa w czasie 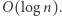 Polega ona na tym, że najpierw liczymy (podnosząc do kwadratu kolejne elementy) wartości
Polega ona na tym, że najpierw liczymy (podnosząc do kwadratu kolejne elementy) wartości
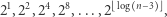 |
a następnie zapisujemy 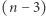 w systemie binarnym, dzięki czemu ustalamy, iloczyn których potęg dwójki da nam
w systemie binarnym, dzięki czemu ustalamy, iloczyn których potęg dwójki da nam 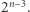 Na przykład jeśli
Na przykład jeśli  to
to
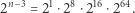 |
Uwaga: wszystkie mnożenia wykonujemy oczywiście modulo 998244353.
2. Jak szybko obliczyć 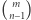 (modulo 998244353)?
(modulo 998244353)?
Dwumian Newtona można obliczać wprost z rekurencji
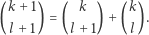 |
Ta metoda, zastosowana jednak bezpośrednio, skończy się czasem wykładniczym. Ulepszenie, polegające na spamiętywaniu już obliczonych wartości (tak zwane programowanie dynamiczne), da złożoność kwadratową, która wciąż będzie za duża, aby rozwiązanie przeszło skutecznie testy sprawdzające.
Skorzystamy więc z wzoru 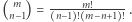
Ponownie, proponujemy aby najpierw wykonać obliczenia wstępne i obliczyć (żargonowo: spamiętać):
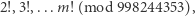 |
ale także (pomijamy, jak dokładnie to zrobić)
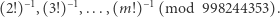 |
Uwaga: chodzi oczywiście o odwrotność w ciele 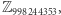 czyli np.
czyli np. 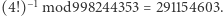
Wyposażeni w powyższe dane już łatwo (w czasie 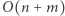 ) możemy obliczyć
) możemy obliczyć 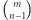 mod 998244353.
mod 998244353.
Powyższe rozwiązanie już jest wystarczające, bo we wszystkich testach mamy 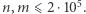 Co jednak, gdybyśmy chcieli rozwiązać zadania dla parametrów rzędu nawet kilku miliardów? Tutaj możemy sobie poradzić za pomocą następującego Olimpijskiego Triku:
Co jednak, gdybyśmy chcieli rozwiązać zadania dla parametrów rzędu nawet kilku miliardów? Tutaj możemy sobie poradzić za pomocą następującego Olimpijskiego Triku:
Zanim zaczniemy pisać program właściwy, możemy obliczyć np. co milionową silnię (i jej odwrotność) modulo 998244353, a wyniki (wygenerowane choćby i przez godzinę w trakcie zawodów) zapisać BEZPOŚREDNIO W KODZIE rozwiązania jako stałą tablicę!
Wówczas kod programu może być ogromny, osiągając nawet kilkadziesiąt kilobajtów tekstu (co wciąż mieści się w regulaminowym limicie!). Dzięki temu same obliczenia właściwe po odczycie danych wejściowych podczas testów będą znacznie szybsze, bo fazy obliczania kolejnych silni nie musimy zaczynać od 2 tylko od najbliższej wielokrotności miliona!
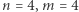 to:
to: 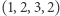 ,
, 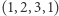 ,
, 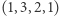 ,
, 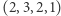 ,
, 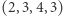 ,
, 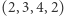 ,
,  ,
, 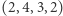 ,
, 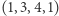 ,
, 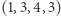 ,
, 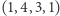 ,
, 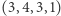 ,
, 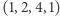 ,
, 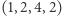 ,
, 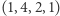 ,
,