Informatyczny kącik olimpijski
Little Elephant and Array
Zadanie. Dany jest 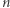 -elementowy ciąg liczb naturalnych
-elementowy ciąg liczb naturalnych 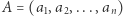 oraz
oraz 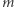 zapytań. Każde zapytanie jest opisane za pomocą dwóch liczb naturalnych
zapytań. Każde zapytanie jest opisane za pomocą dwóch liczb naturalnych 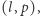 gdzie
gdzie 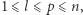 i brzmi: "Ile jest dobrych liczb w podsłowie
i brzmi: "Ile jest dobrych liczb w podsłowie 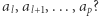 " Liczba
" Liczba 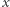 jest dobra, jeśli występuje dokładnie
jest dobra, jeśli występuje dokładnie  razy. Przykładowo, wynikiem dla podkreślonego fragmentu
razy. Przykładowo, wynikiem dla podkreślonego fragmentu 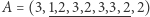 jest 2, gdyż dobrymi liczbami są 1 (występuje raz) oraz 3 (występuje trzy razy). Napisz program, który odpowiada na wszystkie
jest 2, gdyż dobrymi liczbami są 1 (występuje raz) oraz 3 (występuje trzy razy). Napisz program, który odpowiada na wszystkie 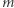 zapytań.
zapytań.
Niech 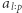 oznacza podsłowo
oznacza podsłowo 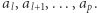
Dowód. Rozwiązanie 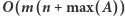
W pierwszym podejściu każde zapytanie rozważymy niezależnie. Załóżmy, że szukamy wyniku dla 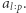 Na początku zliczmy wystąpienia każdej wartości w tym podsłowie. Niech
Na początku zliczmy wystąpienia każdej wartości w tym podsłowie. Niech 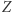 będzie tablicą zliczającą i
będzie tablicą zliczającą i ![Z[x]](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/6x-6baafa12b929f6bdff2e957591141c89e22f7495-im-33,33,33-FF,FF,FF.gif) oznacza liczbę wystąpień
oznacza liczbę wystąpień  Taka tablica ma rozmiar rzędu
Taka tablica ma rozmiar rzędu 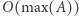 i jej wygenerowanie zajmuje czas
i jej wygenerowanie zajmuje czas 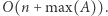 Wówczas wynikiem jest liczba takich
Wówczas wynikiem jest liczba takich 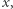 że
że ![|Z[x] = x,](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/11x-6baafa12b929f6bdff2e957591141c89e22f7495-im-33,33,33-FF,FF,FF.gif) co możemy obliczyć w czasie
co możemy obliczyć w czasie 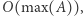 przeglądając
przeglądając 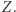 Znalezienie odpowiedzi na jedno zapytanie zajmuje czas
Znalezienie odpowiedzi na jedno zapytanie zajmuje czas 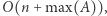 więc całe rozwiązanie działa w czasie
więc całe rozwiązanie działa w czasie 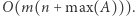
Rozwiązanie 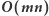
Zauważmy, że dobre liczby są nie większe niż 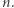 Żadna liczba większa niż
Żadna liczba większa niż 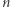 nie może być dobra, ponieważ długość ciągu (liczba wszystkich wystąpień) wynosi
nie może być dobra, ponieważ długość ciągu (liczba wszystkich wystąpień) wynosi 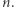 Zatem zliczanie wystąpień możemy ograniczyć do wartości nie większych niż
Zatem zliczanie wystąpień możemy ograniczyć do wartości nie większych niż 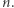 Teraz tablica zliczająca ma rozmiar
Teraz tablica zliczająca ma rozmiar 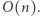 Odpowiedź na jedno zapytanie realizujemy w czasie
Odpowiedź na jedno zapytanie realizujemy w czasie 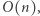 a całe rozwiązanie działa w czasie
a całe rozwiązanie działa w czasie 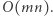
Rozwiązanie 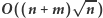
W tym podejściu, przed przystąpieniem do odpowiadania na zapytania, znajdziemy zbiór 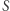 zawierający kandydatów na dobre liczby. Kandydatami mogą być tylko takie liczby
zawierający kandydatów na dobre liczby. Kandydatami mogą być tylko takie liczby 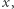 które występują przynajmniej
które występują przynajmniej 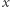 razy w całym ciągu. Tak jak wcześniej zauważyliśmy, możemy ograniczyć zliczanie do wartości nie większych niż
razy w całym ciągu. Tak jak wcześniej zauważyliśmy, możemy ograniczyć zliczanie do wartości nie większych niż 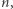 zatem
zatem 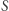 generujemy w czasie
generujemy w czasie 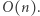 Okazuje się, że wszystkich kandydatów jest nie więcej niż
Okazuje się, że wszystkich kandydatów jest nie więcej niż 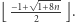
Dlaczego? 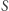 zawiera różne liczby, a jego suma jest nie większa niż
zawiera różne liczby, a jego suma jest nie większa niż 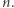 Zbiór ma największą moc, kiedy zawiera kolejne liczby
Zbiór ma największą moc, kiedy zawiera kolejne liczby 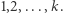 Niech
Niech 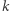 oznacza największą spośród nich. Oczywiście musi zachodzić
oznacza największą spośród nich. Oczywiście musi zachodzić 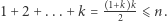 Wystarczy skorzystać ze standardowych metod rozwiązywania nierówności drugiego stopnia, aby otrzymać, że największe
Wystarczy skorzystać ze standardowych metod rozwiązywania nierówności drugiego stopnia, aby otrzymać, że największe 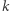 wynosi
wynosi 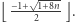
Dla każdej liczby  ze zbioru
ze zbioru 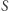 przygotujmy tablicę
przygotujmy tablicę 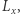 gdzie
gdzie ![|L [i] = 1, x](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/4x-a2a324d4a2f9cc446b3a07e3fee71703684b7812-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 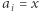 lub
lub ![L [i] = 0 x](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/6x-a2a324d4a2f9cc446b3a07e3fee71703684b7812-im-33,33,33-FF,FF,FF.gif) w przeciwnym przypadku. Intuicyjnie mówiąc, skopiowaliśmy ciąg
w przeciwnym przypadku. Intuicyjnie mówiąc, skopiowaliśmy ciąg 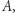 zamieniając wystąpienia
zamieniając wystąpienia 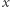 na 1, zaś pozostałe liczby na 0. Dodatkowo, niech
na 1, zaś pozostałe liczby na 0. Dodatkowo, niech 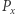 będzie tablicą sum prefiksowych
będzie tablicą sum prefiksowych 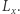 Wówczas sprawdzenie, czy
Wówczas sprawdzenie, czy 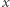 jest dobrą liczbą
jest dobrą liczbą 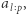 sprowadza się do obliczenia
sprowadza się do obliczenia ![L [l] +L [l + 1] +...+ L [p] = P [p]− P [l −1]. x x x x x](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/13x-a2a324d4a2f9cc446b3a07e3fee71703684b7812-im-33,33,33-FF,FF,FF.gif) Za pomocą tak przygotowanej struktury danych potrafimy w czasie
Za pomocą tak przygotowanej struktury danych potrafimy w czasie 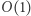 sprawdzić, czy kandydat jest dobrą liczbą w podsłowie. Aby znaleźć dobre liczby w
sprawdzić, czy kandydat jest dobrą liczbą w podsłowie. Aby znaleźć dobre liczby w 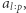 wystarczy sprawdzić kandydatów ze zbioru
wystarczy sprawdzić kandydatów ze zbioru 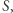 których jest
których jest 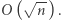 Wyznaczenie odpowiedzi na
Wyznaczenie odpowiedzi na 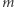 zapytań zajmuje czas
zapytań zajmuje czas 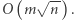 Przygotowanie opisanych struktur danych zajmuje czas
Przygotowanie opisanych struktur danych zajmuje czas 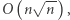 zatem całe rozwiązanie działa w czasie
zatem całe rozwiązanie działa w czasie 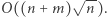
Rozwiązanie 
W tym rozwiązaniu odpowiemy na zapytania offline. Oznacza to, że najpierw wczytamy wszystkie zapytania, następnie obliczymy wyniki (być może w innej kolejności niż ta podana na wejściu) i na końcu wypiszemy odpowiedzi w pierwotnej kolejności zapytań. Najpierw pogrupujmy zapytania według ich końców. Niech ![|zap[i]](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/2x-1426de46bc7415c9efbac5263674317e609c4265-im-33,33,33-FF,FF,FF.gif) oznacza zapytania, których koniec znajduje się w
oznacza zapytania, których koniec znajduje się w  Przejdźmy teraz do przeglądania kolejnych elementów ciągu według rosnących indeksów (od 1 do
Przejdźmy teraz do przeglądania kolejnych elementów ciągu według rosnących indeksów (od 1 do  ). Załóżmy, że rozważamy indeks
). Załóżmy, że rozważamy indeks 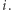 Jeśli wartość
Jeśli wartość 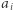 występowała wcześniej przynajmniej
występowała wcześniej przynajmniej 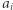 razy, to
razy, to 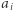 jest dobrą liczbą dla niektórych fragmentów. Dokładniej, niech
jest dobrą liczbą dla niektórych fragmentów. Dokładniej, niech 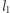 oznacza najmniejszy taki indeks, że
oznacza najmniejszy taki indeks, że 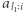 zawiera
zawiera 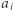 wystąpień
wystąpień 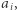 oraz niech
oraz niech 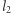 oznacza największy taki indeks, że
oznacza największy taki indeks, że 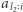 zawiera
zawiera 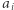 wystąpień
wystąpień 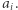 Te indeksy możemy wyznaczyć, mając dla każdej wartości zapamiętane pozycje, na których ta wartość występuje. Wówczas dla każdego
Te indeksy możemy wyznaczyć, mając dla każdej wartości zapamiętane pozycje, na których ta wartość występuje. Wówczas dla każdego 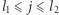 fragment
fragment 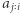 również zawiera
również zawiera 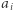 jako dobrą liczbę.
jako dobrą liczbę.
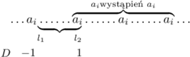
Zachowajmy tę informację w tablicy 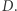 Niech
Niech ![|D[l1− 1] = − 1,](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/2x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) zaś
zaś ![|D[l2] = 1.](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/3x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) Warto nadmienić, że jeśli wcześniej mieliśmy wyznaczony przedział
Warto nadmienić, że jeśli wcześniej mieliśmy wyznaczony przedział ![[l′;l′], 1 2](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/4x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) gdzie mogło zaczynać się podsłowo z dobrą wartością
gdzie mogło zaczynać się podsłowo z dobrą wartością 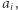 to należy usunąć ten przedział przed nowym przypisaniem, czyli
to należy usunąć ten przedział przed nowym przypisaniem, czyli ![|D[l1′−1] = 0](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/6x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![D[l′2] = 0.](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/7x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) Teraz możemy już odpowiedzieć na zapytania
Teraz możemy już odpowiedzieć na zapytania ![|zap[i].](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/8x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) Załóżmy, że rozważamy zapytanie
Załóżmy, że rozważamy zapytanie 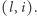 Wtedy wynikiem jest
Wtedy wynikiem jest ![D[l]+ D[l + 1]+ ...+ D[i] .](/math/temat/informatyka/algorytmy/2020/02/29/little-elephant-and-array/10x-59a6dc22682a692ba6e601e31ec6d86263835fde-im-33,33,33-FF,FF,FF.gif) Na
Na 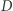 możemy rozpiąć drzewo przedziałowe, aby w czasie
możemy rozpiąć drzewo przedziałowe, aby w czasie 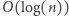 obliczać sumę i aktualizować wartości.
obliczać sumę i aktualizować wartości.
Grupowanie zapytań według ich końca realizujemy w czasie 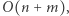 jeśli wykorzystamy metodę zliczania. Odpowiedź na zapytanie odbywa się w czasie
jeśli wykorzystamy metodę zliczania. Odpowiedź na zapytanie odbywa się w czasie 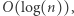 co w sumie dla
co w sumie dla 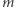 zapytań daje
zapytań daje 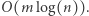 Wszystkie aktualizacje
Wszystkie aktualizacje 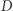 zajmują
zajmują 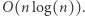 Całkowita złożoność czasowa rozwiązania wynosi
Całkowita złożoność czasowa rozwiązania wynosi