Informatyczny kącik olimpijski
Cyfrowy ciąg
W tym odcinku omówimy rozwiązanie zadania "Cyfrowy ciąg", które pojawiło się w eliminacjach do zawodów Romanian Master of Informatics.
Zadanie (Cyfrowy ciąg). Tadek napisał ciąg 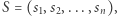 złożony z
złożony z 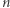 cyfr od
cyfr od 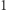 do
do 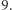 Chciałby podzielić ten ciąg na
Chciałby podzielić ten ciąg na 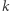 spójnych fragmentów. Każdy fragment czytany od lewej do prawej tworzy liczbę. Tadek chciałby dokonać takiego podziału, aby największa z
spójnych fragmentów. Każdy fragment czytany od lewej do prawej tworzy liczbę. Tadek chciałby dokonać takiego podziału, aby największa z 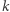 otrzymanych liczb była jak najmniejsza.
otrzymanych liczb była jak najmniejsza.
Niech ![|S[a b]](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/1x-4f0fc5cb17e5a75877bf436429ff052b6cbf178c-im-33,33,33-FF,FF,FF.gif) oznacza fragment
oznacza fragment 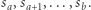
Zauważmy, że 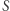 zawiera tylko cyfry od
zawiera tylko cyfry od 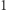 do
do 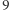 - nie ma cyfry
- nie ma cyfry 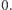 Zatem dowolny jego fragment opisuje liczbę bez zer wiodących. Od tego momentu zakładamy, że rozważamy tylko liczby bez zer wiodących. Wiadomo, że dłuższa liczba jest większa niż krótsza. W związku z tym chcemy tak podzielić ciąg, aby największa liczba była możliwie najkrótsza. Największa liczba zawiera przynajmniej
Zatem dowolny jego fragment opisuje liczbę bez zer wiodących. Od tego momentu zakładamy, że rozważamy tylko liczby bez zer wiodących. Wiadomo, że dłuższa liczba jest większa niż krótsza. W związku z tym chcemy tak podzielić ciąg, aby największa liczba była możliwie najkrótsza. Największa liczba zawiera przynajmniej 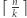 cyfr. Zauważmy, że w jakimś optymalnym podziale będą wyłącznie liczby
cyfr. Zauważmy, że w jakimś optymalnym podziale będą wyłącznie liczby 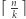 -cyfrowe lub
-cyfrowe lub 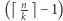 -cyfrowe. Dokładniej, w jakimś optymalnym podziale będzie:
-cyfrowe. Dokładniej, w jakimś optymalnym podziale będzie:
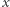 liczb
liczb 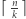 -cyfrowych, gdzie
-cyfrowych, gdzie 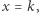 jeśli
jeśli 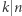 i
i 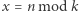 w przeciwnym przypadku,
w przeciwnym przypadku,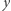 liczb
liczb 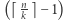 -cyfrowych, gdzie
-cyfrowych, gdzie 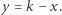
Niech 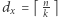 oraz
oraz 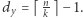 Szukamy takiego podziału
Szukamy takiego podziału 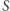 na
na  liczb
liczb 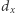 -cyfrowych i
-cyfrowych i 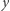 liczb
liczb 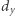 -cyfrowych, żeby największa liczba była jak najmniejsza.
-cyfrowych, żeby największa liczba była jak najmniejsza.
Rozwiązanie 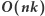
Ten problem możemy rozwiązać za pomocą metody programowania dynamicznego. Otóż niech ![P[i][ j] |D](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/2x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) oznacza wartość największej liczby w optymalnym podziale
oznacza wartość największej liczby w optymalnym podziale 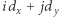 pierwszych cyfr ciągu na
pierwszych cyfr ciągu na 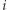 liczb
liczb 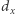 -cyfrowych oraz
-cyfrowych oraz 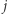 liczb
liczb 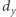 -cyfrowych. Wyznaczymy wartości
-cyfrowych. Wyznaczymy wartości ![P[i][ j]D](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/8x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) dla wszystkich takich
dla wszystkich takich 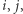 że
że 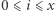 oraz
oraz 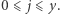 Wówczas wynikiem będzie
Wówczas wynikiem będzie ![P[x][y]. |D](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/12x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) Niech
Niech ![P[0][0]=0, |D](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/13x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) zaś
zaś ![P[i][ j]=min(p,p) |D 12](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/14x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif)
dla 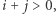 gdzie:
gdzie:
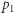 to wynik podziału przy założeniu, że ostatnia liczba ma
to wynik podziału przy założeniu, że ostatnia liczba ma 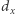 cyfr. Wtedy
cyfr. Wtedy ![P[i−1][ j],S[1+(i−1)d+ jd id+ jd]), p = max(D xyxy 1](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/19x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 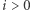
i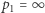 w przeciwnym przypadku.
w przeciwnym przypadku.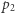 to wynik podziału przy założeniu, że ostatnia liczba ma
to wynik podziału przy założeniu, że ostatnia liczba ma 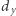 cyfr. Wtedy
cyfr. Wtedy ![P[i][ j−1],S[1+idx+( j−1)dy idx+ jdy]), p2 = max(D](/math/temat/informatyka/algorytmy/2019/11/29/Cyfrowy_ciag/25x-bcb97a70b729f7d5b1b3942f76c74d1ac36840ba-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 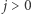
i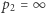 w przeciwnym przypadku.
w przeciwnym przypadku.
Mamy 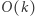 liczb "dłuższych" oraz
liczb "dłuższych" oraz 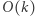 liczb "krótszych", czyli wszystkich stanów do obliczenia jest
liczb "krótszych", czyli wszystkich stanów do obliczenia jest 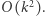 Obliczenie jednego stanu zajmuje
Obliczenie jednego stanu zajmuje 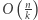 (porównanie dwóch liczb długości
(porównanie dwóch liczb długości 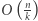 ). Zatem całe rozwiązanie działa w czasie
). Zatem całe rozwiązanie działa w czasie 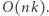
Rozwiązanie 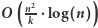
W tym rozwiązaniu wykorzystamy algorytm wyszukiwania binarnego. Wiemy, że wynikiem jest wartość jakiegoś podsłowa długości 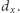 W pierwszej fazie rozwiązania weźmy wszystkie
W pierwszej fazie rozwiązania weźmy wszystkie 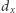 -cyfrowe podsłowa i uporządkujmy je niemalejąco. Takich liczb jest
-cyfrowe podsłowa i uporządkujmy je niemalejąco. Takich liczb jest 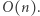 Ich posortowanie wymaga
Ich posortowanie wymaga 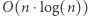 porównań, zaś jedno porównanie zajmuje czas
porównań, zaś jedno porównanie zajmuje czas 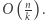 Zatem pierwsza faza działa w czasie
Zatem pierwsza faza działa w czasie 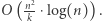
Kiedy mamy już uporządkowany ciąg i wiemy, że jedna z tych liczb jest wynikiem, to możemy wykonać w tym ciągu wyszukiwanie binarne - drugą fazę rozwiązania. Załóżmy, że w kroku algorytmu sprawdzamy, czy wynik jest nie większy niż 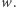 Zatem chcemy dowiedzieć się, czy istnieje podział ciągu na co najwyżej
Zatem chcemy dowiedzieć się, czy istnieje podział ciągu na co najwyżej 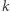 liczb nie większych niż
liczb nie większych niż  W tym celu będziemy dokonywali podziału od lewej do prawej. W każdym kroku zachłannie wybieramy największą możliwą liczbę. Jeśli liczba tworzona przez
W tym celu będziemy dokonywali podziału od lewej do prawej. W każdym kroku zachłannie wybieramy największą możliwą liczbę. Jeśli liczba tworzona przez 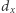 kolejnych cyfr jest nie większa niż
kolejnych cyfr jest nie większa niż 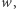 to dodajemy ją do podziału. W przeciwnym przypadku dodajemy liczbę o jeden krótszą. Jeśli po
to dodajemy ją do podziału. W przeciwnym przypadku dodajemy liczbę o jeden krótszą. Jeśli po 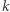 krokach wykorzystamy wszystkie cyfry, to znaleźliśmy podział o wyniku co najwyżej
krokach wykorzystamy wszystkie cyfry, to znaleźliśmy podział o wyniku co najwyżej 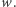
Algorytm wyszukiwania binarnego wykona 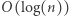 kroków. W każdym kroku przechodzimy po całym ciągu, co zajmuje
kroków. W każdym kroku przechodzimy po całym ciągu, co zajmuje 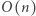 operacji. Zatem druga faza działa w czasie
operacji. Zatem druga faza działa w czasie 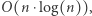 a w całym rozwiązaniu wykonuje się
a w całym rozwiązaniu wykonuje się 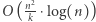 operacji.
operacji.
Rozwiązanie 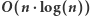
Spróbujmy przyspieszyć pierwszą fazę poprzedniego rozwiązania. W tym celu wykorzystamy słownik podsłów bazowych, którego konstrukcja wymaga 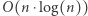 operacji. Za pomocą tej struktury danych możemy w czasie
operacji. Za pomocą tej struktury danych możemy w czasie 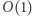 porównać leksykograficznie dwa podsłowa, co jest równoważne porównaniu wartości liczbowych przez nie reprezentowanych. A więc pierwszą fazę rozwiązania wykonujemy w czasie
porównać leksykograficznie dwa podsłowa, co jest równoważne porównaniu wartości liczbowych przez nie reprezentowanych. A więc pierwszą fazę rozwiązania wykonujemy w czasie 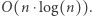
Wersja trudniejsza - cyfry na okręgu
Dla ambitnych Czytelników proponujemy trudniejszą wersję zadania - cyfry są ułożone na okręgu, który możemy rozciąć w dowolnym miejscu. Przedstawimy krótki zarys rozwiązania. Zduplikujmy ciąg 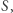 sklejając dwie jego kopie. W ten sposób każde podsłowo długości
sklejając dwie jego kopie. W ten sposób każde podsłowo długości 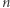 opisuje jakąś rotację cykliczną
opisuje jakąś rotację cykliczną 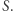 Wynik będziemy wyszukiwali binarnie (jak w poprzednim rozwiązaniu). W każdym kroku, dla każdej pozycji wyznaczamy najdalszą pozycję na prawo, gdzie może zaczynać się kolejna liczba. Jeśli pozycje zinterpretujemy jako wierzchołki, a przejścia do kolejnych liczb jako krawędzie, to otrzymamy graf acykliczny. Pytamy, czy w takim grafie istnieje
Wynik będziemy wyszukiwali binarnie (jak w poprzednim rozwiązaniu). W każdym kroku, dla każdej pozycji wyznaczamy najdalszą pozycję na prawo, gdzie może zaczynać się kolejna liczba. Jeśli pozycje zinterpretujemy jako wierzchołki, a przejścia do kolejnych liczb jako krawędzie, to otrzymamy graf acykliczny. Pytamy, czy w takim grafie istnieje 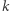 -krawędziowa ścieżka, która pokrywa
-krawędziowa ścieżka, która pokrywa 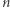 liter. Można to sprawdzić metodą skoków potęgami dwójki.
liter. Można to sprawdzić metodą skoków potęgami dwójki.