O dziesiątym problemie Hilberta

Podczas odbywającego się w 1900 roku w Paryżu Drugiego Międzynarodowego Kongresu Matematyków jeden z referatów wygłosił wybitny niemiecki matematyk David Hilbert. W swoim wystąpieniu zawarł on listę dwudziestu trzech zagadnień matematycznych stanowiących, jego zdaniem, szczególne wyzwanie dla matematyków w rozpoczynającym się XX wieku. Większość z nich doczekała się rozwiązania. Inne, jak słynna hipoteza Riemanna, pozostają otwarte, inspirując kolejne pokolenia naukowców.

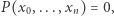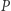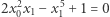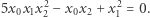Dziesiąty spośród problemów Hilberta dotyczy równań diofantycznych, czyli równań postaci $P(x0,...,xn) = 0,$ gdzie $P$ jest wielomianem o współczynnikach całkowitych. Przykładem równania diofantycznego jest więc $2x2x −x5 + 1 = 0 0 1 1$ oraz $|5x x x2− x x + x2 = 0. 0 1 2 0 2 1$ Hilbert postulował znalezienie procedury, która pozwalałaby dla dowolnego równania diofantycznego rozstrzygnąć w skończonej liczbie kroków, czy równanie to ma rozwiązanie w zbiorze liczb naturalnych, czy też nie. Problem ten jest o tyle wyjątkowy, że jako jedyny na liście Hilberta odwołuje się do pojęcia algorytmu, które na przełomie XIX i XX wieku nie miało jeszcze formalnej definicji. W przypadku wynalezienia postulowanej metody (czego, jak możemy się domyślać, spodziewał się Hilbert) byłoby intuicyjnie jasne, że stanowi ona pozytywne rozwiązanie problemu. Negatywne rozwiązanie dziesiątego problemu Hilberta nie byłoby jednak możliwe bez doprecyzowania jego sformułowania w języku matematycznym.

Współcześnie powszechnie przyjęte definicje pozwalają w sposób całkowicie formalny stwierdzić, że nie istnieje algorytm, który mając dane na wejściu równanie diofantyczne, rozstrzyga, czy ma ono rozwiązanie w liczbach naturalnych. Negatywne rozwiązanie dziesiątego problemu Hilberta jest konsekwencją słynnego twierdzenia z roku 1970, wieńczącego wiele lat pracy czwórki matematyków: Jurija Matijasiewicza, Julii Robinson, Martina Davisa oraz Hilarego Putnama.

Celem tego artykułu jest sformułowanie tak zwanego twierdzenia MRDP (od Matijasiewicz, Robinson, Davis, Putnam), wyjaśnienie zawartej w nim fascynującej idei rozwiązania dziesiątego problemu Hilberta oraz przedstawienie pewnych jego zaskakujących konsekwencji.

Intuicyjnie, algorytm to po prostu skończony zbiór instrukcji. Powszechnie znany jest algorytm dodawania pisemnego, zwany "dodawaniem pod kreską", czy też algorytm Euklidesa wyznaczania największego wspólnego dzielnika dwóch liczb. Pojęcie algorytmu zostało sformalizowane w latach trzydziestych XX wieku niezależnie przez Kurta Gödla, Alana Turinga, Emila Posta oraz Alonzo Churcha. Zaproponowane definicje, na pozór bardzo różne, okazały się równoważne i stanowią dziś podstawę zarówno sposobu funkcjonowania komputerów, jak i teoretycznych badań nad ich możliwościami. Na potrzeby tego artykułu pozostańmy jednak przy intuicyjnym rozumieniu pojęcia algorytmu, pamiętając, że kryje się za nim dobrze zdefiniowany obiekt matematyczny.

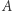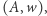Wracając do zagadnienia, z którym mierzyli się Matijasiewicz, Robinson, Davis oraz Putnam - w języku współczesnej informatyki dotyczy ono tak zwanego problemu decyzyjnego: chcemy wiedzieć, które elementy zbioru $|A$ mają interesującą nas własność $|w.$ Dziesiąty problem Hilberta to problem decyzyjny $,w), (A$ gdzie zbiór 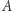$A |$ to zbiór wszystkich równań diofantycznych, a własność 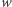$w$ to posiadanie co najmniej jednego rozwiązania w liczbach naturalnych. Innym znanym przykładem problemu decyzyjnego jest problem pierwszości: interesuje nas w tym przypadku zbiór 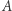$|A$ wszystkich liczb naturalnych oraz własność 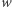$w$ bycia liczbą pierwszą.

Problem decyzyjny 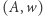$,w) (A$ jest rozstrzygalny, jeśli istnieje algorytm, który, mając dany na wejściu dowolny element 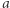$a |$ zbioru 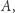$, A$ po wykonaniu skończonej liczby operacji rozstrzyga, czy element 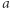$a$ ma własność 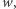$|w,$ czy też nie. Bezpośrednią konsekwencją twierdzenia MRDP (do którego sformułowania zmierzają nasze rozważania) jest nierozstrzygalność dziesiątego problemu Hilberta.

Zwróćmy jednak uwagę, że zdefiniowane powyżej pojęcie rozstrzygalności jest stosunkowo restrykcyjne. Mniej satysfakcjonujące rozwiązanie problemu decyzyjnego 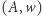$,w) (A$ otrzymamy, wymagając jedynie, żeby algorytm po skończonej liczbie kroków zwrócił pozytywną odpowiedź dokładnie wtedy, gdy na wejściu ma dany element zbioru 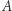$A |$ o własności 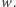$w.$ Natomiast jeśli dany element nie spełnia $|w,$ to algorytm może się nie zatrzymać. Problem decyzyjny, dla którego taki algorytm istnieje, nazywamy częściowo rozstrzygalnym. Łatwo stwierdzić, że dziesiąty problem Hilberta jest częściowo rozstrzygalny: wystarczy rozważyć algorytm, który dla danego równania diofantycznego sprawdza po kolei wszystkie możliwe wartościowania w liczbach naturalnych występującego w nim zbioru niewiadomych. Jeśli któreś z kolei wartościowanie spełni równanie, algorytm zwraca odpowiedź pozytywną, natomiast w przeciwnym przypadku nigdy nie zakończy on swojego działania.

Dziesiąty problem Hilberta jest więc przykładem problemu decyzyjnego, który jest częściowo rozstrzygalny, ale nie jest rozstrzygalny. Wynika to jednak dopiero z udowodnionego w 1970 roku twierdzenia MRDP. Na długo przed rokiem 1970 matematycy zdawali sobie sprawę z istnienia częściowo rozstrzygalnych, ale nierozstrzygalnych problemów decyzyjnych postaci $|(N,w),$ gdzie $w |$ jest pewną własnością liczb naturalnych. Twierdzenie MRDP potwierdza odważną hipotezę, według której zbiór wszystkich częściowo rozstrzygalnych problemów decyzyjnych dotyczących liczb naturalnych jest w pewien sposób silnie powiązany ze zbiorem równań diofantycznych.

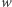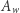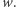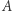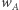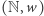Każda własność $w |$ liczb naturalnych definiuje podzbiór $A | w$ liczb naturalnych o własności $w. |$ Jednocześnie, każdy podzbiór $A |$ liczb naturalnych definiuje własność $|wA$ należenia do podzbioru $. A |$ Upraszczając nieco terminologię, zamiast o rozstrzygalnych lub częściowo rozstrzygalnych problemach decyzyjnych postaci $(N, w)$ możemy więc mówić o rozstrzygalnych lub częściowo rozstrzygalnych podzbiorach zbioru liczb naturalnych. W 1950 roku Martin Davis sformułował hipotezę, zgodnie z którą każdy częściowo rozstrzygalny podzbiór zbioru liczb naturalnych jest tak zwanym zbiorem diofantycznym.

Definicja zbioru diofantycznego wymaga rozważenia równań diofantycznych z parametrem. Parametrem nazwiemy po prostu jedną, wyróżnioną niewiadomą. 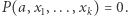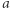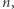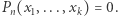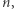Równanie diofantyczne z parametrem jest więc postaci $|P(a,x1,...,xk) = 0.$ Definiuje ono całą rodzinę równań diofantycznych: podstawiając za parametr $a$ dowolną liczbę naturalną $|n,$ otrzymamy równanie diofantyczne (bez parametru), które oznaczać będziemy przez $|Pn(x1,...,xk) = 0.$ Dla dowolnego równania diofantycznego z parametrem $|P(a,x1,...,xk) = 0,$ zbiór tych liczb naturalnych $n,$ dla których równanie 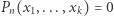$|Pn(x1,...,xk) = 0$ ma rozwiązanie w liczbach naturalnych, nazywamy zbiorem diofantycznym. Przykładem zbioru diofantycznego jest zatem zbiór drugich potęg liczb naturalnych odpowiadający równaniu 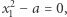$|x21− a = 0,$ a także zbiór liczb złożonych odpowiadający równaniu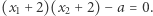 $|(x1 + 2)(x2 + 2)− a = 0.$

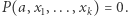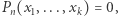Zauważmy, że każdy zbiór diofantyczny jest częściowo rozstrzygalny. Rzeczywiście, przypuśćmy, że mamy dany zbiór diofantyczny zadany przez równanie diofantyczne z parametrem $|P(a,x ,...,x ) = 0. 1 k$ Algorytm świadczący o tym, że zbiór ten jest częściowo rozstrzygalny, dla danej na wejściu liczby naturalnej $n$ oblicza równanie diofantyczne $|Pn(x1,...,xk) = 0,$ a następnie sprawdza po kolei wszystkie wartościowania jego niewiadomych w liczbach naturalnych. Jeśli któreś wartościowanie spełni równanie 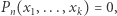$|Pn(x1,...,xk) = 0,$ algorytm zwraca odpowiedź pozytywną, zaś w przeciwnym przypadku nie zakończy on swojego działania.

Hipoteza Davisa, jak już wspomnieliśmy, dotyczy implikacji przeciwnej: każdy częściowo rozstrzygalny podzbiór zbioru liczb naturalnych jest diofantyczny. Została ona udowodniona po dwudziestu latach intensywnych badań. Jej potwierdzenie stanowi treść twierdzenia MRDP, które możemy zatem sformułować następująco:

Twierdzenie (MRDP). Podzbiór zbioru liczb naturalnych jest częściowo rozstrzygalny wtedy i tylko wtedy, gdy jest zbiorem diofantycznym.

Uwzględniając fakt istnienia częściowo rozstrzygalnych, ale nierozstrzygalnych podzbiorów zbioru liczb naturalnych, twierdzenie MRDP implikuje istnienie nierozstrzygalnych zbiorów diofantycznych i w konsekwencji negatywne rozwiązanie dziesiątego problemu Hilberta. Zanim jednak prześledzimy dokładniej tę ostatnią implikację, przyjrzyjmy się, jak zaskakująca jest w istocie treść twierdzenia MRDP.

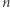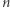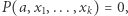Wspomniany powyżej problem pierwszości jest z pewnością rozstrzygalny: dla danej na wejściu liczby naturalnej $n$ trywialny algorytm sprawdza po kolei, czy $|n$ jest podzielne przez jakąkolwiek liczbę ze zbioru $|{2,...,n − 1}.$ W szczególności, zbiór liczb pierwszych jest częściowo rozstrzygalny. Z twierdzenia MRDP wynika zatem, że istnieje równanie diofantyczne z parametrem $|P(a,x ,...,x ) = 0, 1 k$ które ma rozwiązanie w liczbach naturalnych wtedy i tylko wtedy, gdy $|a$ jest liczbą pierwszą! 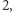Podobnie ma się sprawa ze zbiorem wszystkich potęg liczby $2,$ zbiorem liczb Fibonacciego... i przypuszczalnie z każdym innym podzbiorem zbioru liczb naturalnych, którego definicja przychodzi nam łatwo do głowy.

Pozostaje nam przyjrzeć się, w jaki sposób z twierdzenia MRDP wynika negatywne rozwiązanie dziesiątego problemu Hilberta. Przypuśćmy, że odpowiedź ta byłaby pozytywna, i niech 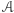$𝒜$ oznacza algorytm, który dla dowolnego równania diofantycznego rozstrzyga, czy ma ono rozwiązanie w liczbach naturalnych, czy też nie. 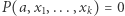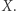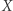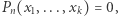Rozważmy równanie diofantyczne z parametrem $P (a,x1,...,xk) = 0$ definiujące pewien zbiór diofantyczny $.X$ Zauważmy, że następujący algorytm rozstrzyga przynależność do zbioru $|X$ : dla danej na wejściu liczby naturalnej $n$ oblicz równanie diofantyczne $|Pn(x1,...,xk) = 0,$ a następnie za pomocą algorytmu 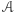$𝒜$ rozstrzygnij, czy ma ono rozwiązanie w zbiorze liczb naturalnych. Odpowiedź pozytywna oznacza, że 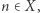$, |n∈ X$ natomiast odpowiedź negatywna oznacza, że 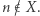$.n /∈ X$ Wykazaliśmy w ten sposób, że każdy zbiór diofantyczny jest rozstrzygalny. Na mocy twierdzenia MRDP oznacza to, że każdy częściowo rozstrzygalny podzbiór zbioru liczb naturalnych jest rozstrzygalny. Otrzymana sprzeczność implikuje nierozstrzygalność dziesiątego problemu Hilberta.

Joanna Ochremniak

Posłowie

Jak uniknąć częściowej rozstrzygalności?

W artykule powyżej wspomniano, że prawie każdy zbiór liczb naturalnych, który przyjdzie nam na myśl, jest częściowo rozstrzygalny. Spróbujmy jednak pokazać, że słowo prawie jest tu istotne, czyli że możliwa jest konstrukcja zbioru 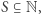$S ⊆ N,$ który nie jest częściowo rozstrzygalny.

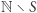Po pierwsze zauważmy, że jeśli zarówno zbiór $S,$ jak i jego dopełnienie $|N ∖S$ są częściowo rozstrzygalne, to wówczas 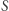$|S$ jest nawet rozstrzygalny. To, że $|S$ jest częściowo rozstrzygalny, oznacza, że istnieje algorytm (nazwijmy go pozytywnym), który dla danej liczby $n ∈ N$ zatrzyma się i odpowie " 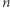$|n$ należy do 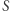$S$ ", jeśli 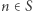$n ∈ S$ (ale być może nie zatrzyma się, jeśli 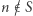$n /∈ S$ ). Podobnie, skoro 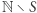$N ∖ S$ jest częściowo rozstrzygalny, to istnieje algorytm (nazwijmy go negatywnym), który dla danej liczby 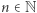$n ∈N$ zatrzyma się i odpowie " 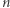$|n$ należy do 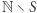$N ∖ S$ ", o ile 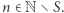$n ∈N ∖ S.$ A zatem jeśli puścimy naraz oba algorytmy, pozytywny i negatywny, to któryś z nich się zatrzyma i zwróci poprawną odpowiedź (zakładamy, że wtedy automatycznie zatrzymujemy również drugi algorytm). To pokazuje, że istotnie w takiej sytuacji $S$ jest rozstrzygalny.

A zatem do konstrukcji zbioru, który nie jest nawet częściowo rozstrzygalny, wystarczy znaleźć $|S⊆ N$ taki, że jest on częściowo rozstrzygalny, ale nie jest rozstrzygalny. Wówczas 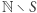$N ∖S$ nie będzie nawet częściowo rozstrzygalny. Aby skonstruować taki zbiór 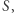$S,$ potrzebna jest pewna wiedza; zakładamy, że Czytelnik Doświadczony zna definicję i podstawowe intuicje związane z maszynami Turinga. Zbiór maszyn Turinga, które akceptują słowo puste, jest częściowo rozstrzygalny (wystarczy znaleźć bieg akceptujący dla tego słowa pustego), ale nie jest rozstrzygalny (uzasadnienie można znaleźć np. w artykule Szymona Toruńczyka Paradoks Russella w Delta 11/2017). Każdą maszynę Turinga można jednoznacznie zakodować jako liczbę naturalną. Zatem zbiór zakodowań maszyn Turinga, które akceptują słowo puste, jest częściowo rozstrzygalny, ale rozstrzygalny już nie jest.

Wojciech Czerwiński