Informatyczny kącik olimpijski
123-Pairs
W tym odcinku omówimy rozwiązanie zadania "123-Pairs", które pojawiło się na "Code Festival 2016".
Zadanie (123-Pairs). Danych jest 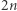 liczb naturalnych od
liczb naturalnych od 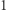 do
do 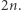 Chcemy połączyć te liczby w
Chcemy połączyć te liczby w 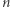 par tak, aby każda liczba należała do dokładnie jednej pary. Dodatkowo, chcemy aby
par tak, aby każda liczba należała do dokładnie jednej pary. Dodatkowo, chcemy aby 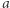 par miało różnicę
par miało różnicę 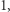
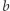 par miało różnicę
par miało różnicę 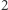 oraz
oraz  par miało różnicę
par miało różnicę 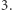 Innych par nie powinno być, tzn.
Innych par nie powinno być, tzn. 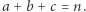 Na ile sposobów można poparować liczby od
Na ile sposobów można poparować liczby od 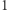 do
do 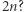 Należy podać resztę z dzielenia wyniku przez
Należy podać resztę z dzielenia wyniku przez 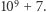
Przedział liczb naturalnych nazwiemy zamkniętym, jeśli liczby z tego przedziału są poparowane. Niech trójka 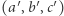 opisuje zamknięty przedział, który zawiera
opisuje zamknięty przedział, który zawiera 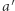 par o różnicy
par o różnicy 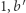 par o różnicy
par o różnicy 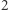 oraz
oraz 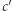 par o różnicy
par o różnicy 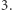
- Cały artykuł dostępny jest w wersji do druku: (316 KB)