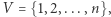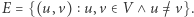Informatyczny kącik olimpijski
Telekomunikacja
W tym odcinku omówimy rozwiązanie zadania "Telekomunikacja", które pojawiło się na drugim etapie Zawodów Drużynowych XIII Młodzieżowej Olimpiady Informatycznej.
Zadanie (Telekomunikacja). W pewnym państwie znajduje się 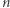 miast ponumerowanych kolejnymi liczbami naturalnymi od
miast ponumerowanych kolejnymi liczbami naturalnymi od 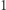 do
do 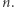 W każdym mieście znajduje się jedna wieża telekomunikacyjna. Wieża w
W każdym mieście znajduje się jedna wieża telekomunikacyjna. Wieża w 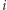 -tym mieście jest przystosowana do nadawania i odbierania fal na częstotliwości
-tym mieście jest przystosowana do nadawania i odbierania fal na częstotliwości 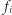 herców. Dotychczas wszystkie miasta komunikowały się bardzo chaotycznie, dlatego postanowiono to uporządkować. Bezpośrednia komunikacja ma być ograniczona do wybranej sieci połączeń. Sieć ma składać się z
herców. Dotychczas wszystkie miasta komunikowały się bardzo chaotycznie, dlatego postanowiono to uporządkować. Bezpośrednia komunikacja ma być ograniczona do wybranej sieci połączeń. Sieć ma składać się z 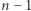 połączeń pomiędzy miastami oraz ma być spójna (innymi słowy ma tworzyć drzewo). Wartością połączenia pomiędzy miastami
połączeń pomiędzy miastami oraz ma być spójna (innymi słowy ma tworzyć drzewo). Wartością połączenia pomiędzy miastami  i
i 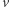 nazywamy największy wspólny dzielnik liczb
nazywamy największy wspólny dzielnik liczb 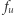 i
i 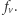 Król chce wybrać taką sieć, aby suma wartości połączeń była maksymalna. Pomóż mu i podaj tę wartość.
Król chce wybrać taką sieć, aby suma wartości połączeń była maksymalna. Pomóż mu i podaj tę wartość.
Wstęp
Zacznijmy od opisania zadania jako problemu grafowego. Dany jest graf pełny 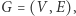 gdzie:
gdzie:
Wagą krawędzi 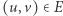 jest
jest 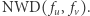 Chcemy znaleźć sumę wag krawędzi maksymalnego drzewa rozpinającego.
Chcemy znaleźć sumę wag krawędzi maksymalnego drzewa rozpinającego.
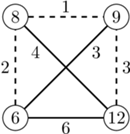
Przykładowo, jeśli mamy cztery miasta, w których wieże nadają z częstotliwościami: 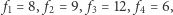 to graf wygląda następująco (linie ciągłe oznaczają krawędzie maksymalnego drzewa rozpinającego, a suma wag tych krawędzi wynosi
to graf wygląda następująco (linie ciągłe oznaczają krawędzie maksymalnego drzewa rozpinającego, a suma wag tych krawędzi wynosi 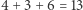 ).
).
Niech 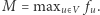
Rozwiązanie 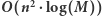
W pierwszym kroku tego rozwiązania zbudujmy wyżej opisany graf, który ma  wierzchołków i
wierzchołków i 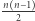 krawędzi. Wagę dowolnej krawędzi
krawędzi. Wagę dowolnej krawędzi 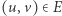 możemy obliczyć za pomocą algorytmu Euklidesa, który działa w czasie
możemy obliczyć za pomocą algorytmu Euklidesa, który działa w czasie 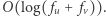 Zatem cały graf zbudujemy w czasie
Zatem cały graf zbudujemy w czasie 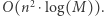
Znajdowanie minimalnego drzewa rozpinającego to znany problem, który może zostać rozwiązany za pomocą jednego z algorytmów: Prima, Kruskala lub Borůvki. Do znalezienia maksymalnego drzewa rozpinającego wykorzystamy zmodyfikowany algorytm Kruskala. Na początku mamy las drzew, gdzie każdy wierzchołek stanowi osobne drzewo. Następnie przeglądamy wszystkie krawędzie w kolejności nierosnących wag. Jeśli rozpatrywana krawędź łączy dwa różne drzewa, to dodajemy ją do drzewa rozpinającego. Sprawdzanie, czy dwa wierzchołki należą do różnych drzew, możemy zrealizować za pomocą struktury zbiorów rozłącznych. Czas wykonania 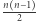 operacji (dla każdej krawędzi) na
operacji (dla każdej krawędzi) na  -elementowym zbiorze wierzchołków wynosi
-elementowym zbiorze wierzchołków wynosi 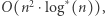 gdzie
gdzie 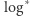 oznacza logarytm iterowany, czyli liczbę operacji logarytmowania potrzebną do uzyskania wyniku nie większego od 1. Algorytm wybierze
oznacza logarytm iterowany, czyli liczbę operacji logarytmowania potrzebną do uzyskania wyniku nie większego od 1. Algorytm wybierze 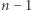 krawędzi, które tworzą maksymalne drzewo rozpinające. Całkowity czas działania algorytmu wynosi
krawędzi, które tworzą maksymalne drzewo rozpinające. Całkowity czas działania algorytmu wynosi 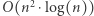 (dominujące jest sortowanie krawędzi po wadze). Jeśli wykorzystamy sortowanie przez zliczanie, to otrzymamy czas
(dominujące jest sortowanie krawędzi po wadze). Jeśli wykorzystamy sortowanie przez zliczanie, to otrzymamy czas 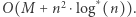 Dowód poprawności algorytmu pozostawiamy Czytelnikowi jako ćwiczenie (dowód jest analogiczny do dowodu algorytmu Kruskala).
Dowód poprawności algorytmu pozostawiamy Czytelnikowi jako ćwiczenie (dowód jest analogiczny do dowodu algorytmu Kruskala).
Rozwiązanie 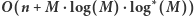
W tym rozwiązaniu nie będziemy jawnie konstruowali grafu, natomiast postaramy się szybko znajdować krawędzie maksymalnego drzewa rozpinającego. Zauważmy, że 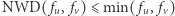 dla dowolnych
dla dowolnych 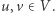 Zatem krawędzie incydentne z wierzchołkiem
Zatem krawędzie incydentne z wierzchołkiem 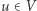 mogą mieć co najwyżej wagę
mogą mieć co najwyżej wagę 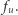 Na mocy obserwacji połączmy w drzewa wierzchołki o tej samej częstotliwości. Niech
Na mocy obserwacji połączmy w drzewa wierzchołki o tej samej częstotliwości. Niech 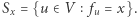 Teraz, dla każdego naturalnego
Teraz, dla każdego naturalnego ![]x∈ [1;M](/math/temat/informatyka/algorytmy/2019/06/30/Telekomunikacja/6x-ae52be0c93a558bf2d99444ae7741a0df45d3149-im-33,33,33-FF,FF,FF.gif) wierzchołki
wierzchołki 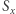 łączymy w drzewo. Wystarczy np. do wybranego wierzchołka podłączyć pozostałe, tworząc
łączymy w drzewo. Wystarczy np. do wybranego wierzchołka podłączyć pozostałe, tworząc 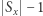 nowych krawędzi o wadze
nowych krawędzi o wadze 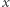 każda. W dalszej części rozwiązania możemy uwzględnić tylko reprezentantów otrzymanych drzew, ponieważ każdy wierzchołek w drzewie ma taki sam zestaw wag krawędzi. Wówczas nie ma dwóch wierzchołków o tym współczynniku.
każda. W dalszej części rozwiązania możemy uwzględnić tylko reprezentantów otrzymanych drzew, ponieważ każdy wierzchołek w drzewie ma taki sam zestaw wag krawędzi. Wówczas nie ma dwóch wierzchołków o tym współczynniku.
W zmodyfikowanym algorytmie Kruskala przeglądamy krawędzie w kolejności nierosnących wag. Zatem dla każdego 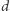 od
od 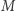 do
do 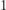 znajdźmy wierzchołki, które mogą być połączone krawędzią o wadze
znajdźmy wierzchołki, które mogą być połączone krawędzią o wadze 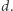 Są to wierzchołki z etykietami:
Są to wierzchołki z etykietami: 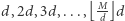 (wielokrotności
(wielokrotności 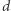 nie większe niż
nie większe niż 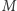 ). Chcemy wszystkie te wierzchołki uspójnić (być może pomiędzy niektórymi wierzchołkami są już krawędzie wygenerowane wcześniej). Wystarczy, że wybierzemy jeden wierzchołek i podłączymy do niego te wierzchołki, które należą do innego drzewa.
). Chcemy wszystkie te wierzchołki uspójnić (być może pomiędzy niektórymi wierzchołkami są już krawędzie wygenerowane wcześniej). Wystarczy, że wybierzemy jeden wierzchołek i podłączymy do niego te wierzchołki, które należą do innego drzewa.
Dla każdego 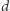 rozpatrzymy
rozpatrzymy 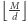 wierzchołków. Zatem w sumie rozpatrzymy
wierzchołków. Zatem w sumie rozpatrzymy 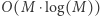 wierzchołków. Do sprawdzania spójności wykorzystujemy strukturę zbiorów rozłącznych. W celu szybkiego sprawdzania, czy istnieje wierzchołek z daną etykietą, wystarczy na początku zliczyć wystąpienia w czasie
wierzchołków. Do sprawdzania spójności wykorzystujemy strukturę zbiorów rozłącznych. W celu szybkiego sprawdzania, czy istnieje wierzchołek z daną etykietą, wystarczy na początku zliczyć wystąpienia w czasie 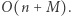 Stąd całkowita złożoność wynosi
Stąd całkowita złożoność wynosi