Informatyczny kącik olimpijski
Trzej znajomi
W tym odcinku omówimy rozwiązanie zadania "Trzej znajomi", które pojawiło się na drugim etapie XIII Młodzieżowej Olimpiady Informatycznej.
Zadanie. Trzej znajomi: Adam, Błażej i Cezary postanowili napisać ciąg 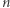 liczb naturalnych. Każdy z nich miał inny pomysł na ciąg. Adam chciał napisać ciąg
liczb naturalnych. Każdy z nich miał inny pomysł na ciąg. Adam chciał napisać ciąg 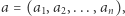 Błażej ciąg
Błażej ciąg 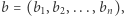 zaś Cezary ciąg
zaś Cezary ciąg 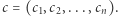 Znajomi długo nie mogli dojść do porozumienia, dlatego postanowili zbudować nowy ciąg
Znajomi długo nie mogli dojść do porozumienia, dlatego postanowili zbudować nowy ciąg 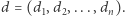 Ustalili, że na każdej pozycji wybiorą którąś ze swoich opcji, czyli
Ustalili, że na każdej pozycji wybiorą którąś ze swoich opcji, czyli 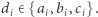 Koledzy zgadzają się, że różnica pomiędzy największym a najmniejszym elementem ciągu
Koledzy zgadzają się, że różnica pomiędzy największym a najmniejszym elementem ciągu 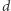 powinna być jak najmniejsza. Jaką najmniejszą różnicę może mieć ciąg
powinna być jak najmniejsza. Jaką najmniejszą różnicę może mieć ciąg 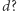
Rozwiązanie 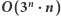
Zacznijmy od rozwiązania, które generuje wszystkie możliwe ciągi 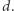 Takich ciągów jest
Takich ciągów jest 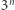 (wartość każdego z
(wartość każdego z  elementów można wybrać na
elementów można wybrać na 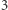 sposoby). Spośród wygenerowanych ciągów należy wybrać ten, który ma najmniejszą różnicę pomiędzy największym a najmniejszym elementem, oraz wypisać tę różnicę. Dla ustalonego ciągu
sposoby). Spośród wygenerowanych ciągów należy wybrać ten, który ma najmniejszą różnicę pomiędzy największym a najmniejszym elementem, oraz wypisać tę różnicę. Dla ustalonego ciągu 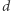 znalezienie najmniejszego i największego elementu można wykonać w czasie
znalezienie najmniejszego i największego elementu można wykonać w czasie 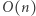 (przeglądamy kolejne elementy, pamiętając najmniejszy oraz największy). Rozwiązanie działa w czasie
(przeglądamy kolejne elementy, pamiętając najmniejszy oraz największy). Rozwiązanie działa w czasie 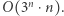
Obserwacja:
Zauważmy, że dla ustalonych całkowitych 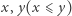 możemy w czasie
możemy w czasie 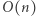 sprawdzić, czy istnieje ciąg
sprawdzić, czy istnieje ciąg 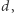 którego wartości elementów należą do przedziału
którego wartości elementów należą do przedziału ![[x; | y].](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/4x-bc4c1cf6b1cf43fbb0eab4225a16aa248962e317-im-33,33,33-FF,FF,FF.gif) Warunkiem koniecznym i wystarczającym jest, aby dla każdego indeksu
Warunkiem koniecznym i wystarczającym jest, aby dla każdego indeksu 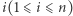 przynajmniej jeden z trzech elementów
przynajmniej jeden z trzech elementów 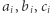 należał do
należał do ![[x;y].](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/7x-bc4c1cf6b1cf43fbb0eab4225a16aa248962e317-im-33,33,33-FF,FF,FF.gif)
Rozwiązanie 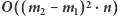
Niech 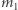 i
i 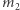 oznaczają odpowiednio wartość najmniejszego i największego elementu w ciągach
oznaczają odpowiednio wartość najmniejszego i największego elementu w ciągach 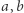 i
i  Korzystając z powyższej obserwacji, wystarczy dla wszystkich par liczb całkowitych
Korzystając z powyższej obserwacji, wystarczy dla wszystkich par liczb całkowitych 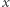 i
i 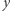
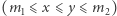 sprawdzić, czy istnieje ciąg
sprawdzić, czy istnieje ciąg 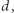 którego wartości należą do przedziału
którego wartości należą do przedziału ![|[x;y].](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/10x-286f45ccc3de29cf3fa1e374d706153b642d24c8-im-33,33,33-FF,FF,FF.gif) Spośród poprawnych przedziałów należy wybrać ten o najmniejszej różnicy
Spośród poprawnych przedziałów należy wybrać ten o najmniejszej różnicy 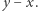 Wszystkich przedziałów do sprawdzenia jest
Wszystkich przedziałów do sprawdzenia jest 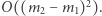 Zatem rozwiązanie zajmuje czas
Zatem rozwiązanie zajmuje czas 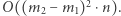
Rozwiązanie 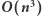
Niech 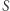 będzie zbiorem wartości, które występują przynajmniej raz w ciągu
będzie zbiorem wartości, które występują przynajmniej raz w ciągu 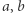 lub
lub  Zauważmy, że wystarczy rozważać tylko takie przedziały
Zauważmy, że wystarczy rozważać tylko takie przedziały ![|[x; y],](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/5x-1f68c035b955230341e7d8c9c75fd8ac112273cd-im-33,33,33-FF,FF,FF.gif) dla których
dla których 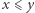 oraz
oraz 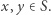 Moc zbioru
Moc zbioru 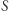 jest rzędu
jest rzędu 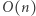 (co najwyżej
(co najwyżej 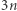 różnych wartości może pojawić się w
różnych wartości może pojawić się w 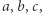 ponieważ tyle jest w sumie elementów). Stąd do sprawdzenia mamy
ponieważ tyle jest w sumie elementów). Stąd do sprawdzenia mamy 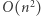 przedziałów, zatem całkowita złożoność czasowa wynosi
przedziałów, zatem całkowita złożoność czasowa wynosi 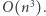
Rozwiązanie 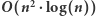
Okazuje się, że nie musimy sprawdzać wszystkich wyżej wymienionych przedziałów. Wystarczy, że dla każdego 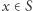 wyznaczymy takie najmniejsze
wyznaczymy takie najmniejsze 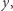 że istnieje ciąg
że istnieje ciąg 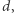 którego wartości elementów należą do
którego wartości elementów należą do ![|[x; y].](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/5x-429565ee0e1f63549d34b4066cf90fc8ecbe9cde-im-33,33,33-FF,FF,FF.gif) Ustalmy
Ustalmy 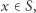 dla którego szukamy najmniejszego
dla którego szukamy najmniejszego 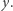 Następnie wartość
Następnie wartość 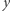 wyszukajmy binarnie w przedziale
wyszukajmy binarnie w przedziale ![|[x;max(S)].](/math/temat/informatyka/algorytmy/2019/05/31/Trzej_znajomi/9x-429565ee0e1f63549d34b4066cf90fc8ecbe9cde-im-33,33,33-FF,FF,FF.gif) Rozwiązanie działa w czasie
Rozwiązanie działa w czasie 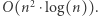
Rozwiązanie 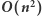
Podobnie jak wyżej, dla każdego 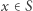 wyznaczymy najmniejsze poprawne
wyznaczymy najmniejsze poprawne 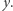 W tym celu skonstruujemy ciąg
W tym celu skonstruujemy ciąg 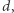 którego największy element będzie możliwie najmniejszy. Dla każdego
którego największy element będzie możliwie najmniejszy. Dla każdego 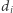 mamy trzech kandydatów
mamy trzech kandydatów 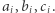 Spośród nich wybieramy najmniejszego, który jest większy lub równy
Spośród nich wybieramy najmniejszego, który jest większy lub równy  Jeśli taki element nie istnieje, to znaczy, że nie istnieje ciąg
Jeśli taki element nie istnieje, to znaczy, że nie istnieje ciąg 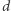 z minimalnym elementem
z minimalnym elementem 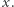 W przeciwnym przypadku
W przeciwnym przypadku 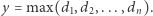 Dla ustalonego
Dla ustalonego 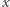 wyznaczenie minimalnego
wyznaczenie minimalnego 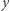 odbywa się w czasie
odbywa się w czasie 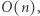 zatem całe rozwiązanie działa w czasie
zatem całe rozwiązanie działa w czasie 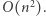
Rozwiązanie 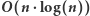
Każdy z elementów ciągów 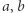 i
i  opiszmy parą liczb: wartość i indeks. W ten sposób otrzymamy
opiszmy parą liczb: wartość i indeks. W ten sposób otrzymamy 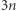 par:
par: 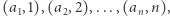
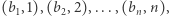
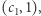
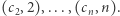 Następnie posortujmy te pary rosnąco względem pierwszej współrzędnej, aby otrzymać ciąg
Następnie posortujmy te pary rosnąco względem pierwszej współrzędnej, aby otrzymać ciąg 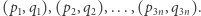 Zauważmy, że z ciągu
Zauważmy, że z ciągu 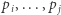 (dla
(dla 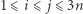 ) można wybrać
) można wybrać  elementów, które utworzą ciąg
elementów, które utworzą ciąg 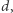 jeśli
jeśli 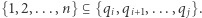 Innymi słowy, dla każdej pozycji (od
Innymi słowy, dla każdej pozycji (od 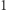 do
do 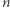 ) musimy ustalić przynajmniej jeden element. Zatem chcemy znaleźć takie indeksy
) musimy ustalić przynajmniej jeden element. Zatem chcemy znaleźć takie indeksy 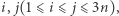 że z
że z 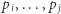 można zbudować ciąg
można zbudować ciąg 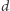 oraz
oraz 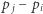 jest minimalne. Wystarczy, że dla każdego
jest minimalne. Wystarczy, że dla każdego 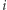 od
od 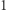 do
do 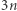 znajdziemy najmniejsze takie
znajdziemy najmniejsze takie 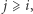 że z elementów
że z elementów 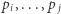 można zbudować ciąg
można zbudować ciąg 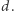 Do rozwiązania tego problemu wykorzystamy metodę gąsienicy. Na początku
Do rozwiązania tego problemu wykorzystamy metodę gąsienicy. Na początku 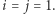 Dopóki fragment
Dopóki fragment 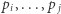 nie pozwala stworzyć poprawnego ciągu, to zwiększamy
nie pozwala stworzyć poprawnego ciągu, to zwiększamy 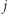 o jeden. W przeciwnym przypadku przechodzimy do kolejnego
o jeden. W przeciwnym przypadku przechodzimy do kolejnego 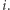 W każdym kroku zliczamy liczbę wystąpień każdego indeksu na rozpatrywanym fragmencie oraz pamiętamy liczbę różnych indeksów, które występują przynajmniej raz. Jeśli ta wartość jest równa
W każdym kroku zliczamy liczbę wystąpień każdego indeksu na rozpatrywanym fragmencie oraz pamiętamy liczbę różnych indeksów, które występują przynajmniej raz. Jeśli ta wartość jest równa 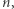 to wtedy rozpatrywany fragment tworzy ciąg
to wtedy rozpatrywany fragment tworzy ciąg 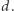
Sortowanie działa w czasie 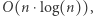 zaś faza szukania najkrótszych fragmentów dla każdego początku zajmuje czas
zaś faza szukania najkrótszych fragmentów dla każdego początku zajmuje czas 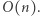 Zatem całe rozwiązanie działa w czasie
Zatem całe rozwiązanie działa w czasie