Informatyczny kącik olimpijski
Klocki z numerami i piłeczki na podłodze
W tym odcinku omówimy rozwiązania dwóch zadań z pierwszego etapu XIII Młodzieżowej Olimpiady Informatycznej.
Zadanie (Klocki z numerami). Danych jest  klocków z zapisanymi na nich numerami. Ciąg
klocków z zapisanymi na nich numerami. Ciąg 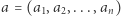 opisuje numery zapisane na kolejnych klockach. Mówimy, że kolekcja klocków jest imponująca, jeśli każdy naturalny numer
opisuje numery zapisane na kolejnych klockach. Mówimy, że kolekcja klocków jest imponująca, jeśli każdy naturalny numer  występuje
występuje  razy albo nie występuje wcale. Imponującymi kolekcjami są
razy albo nie występuje wcale. Imponującymi kolekcjami są 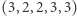 i
i 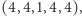 zaś nie są:
zaś nie są: 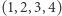 i
i 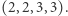 Możemy zmienić numer dowolnego klocka na dowolny inny numer. Ile minimalnie zmian numerów należy dokonać, aby otrzymać imponującą kolekcję?
Możemy zmienić numer dowolnego klocka na dowolny inny numer. Ile minimalnie zmian numerów należy dokonać, aby otrzymać imponującą kolekcję?
Rozwiązanie 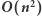
Nasze rozważania rozpocznijmy od prostej obserwacji:
Obserwacja. W ostatecznym ponumerowaniu żaden klocek nie będzie miał numeru większego niż 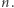
Na mocy powyższej obserwacji możemy ograniczyć się do numerów nie większych niż 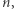 gdyż tylko takie numery będą w ostatecznym ponumerowaniu. Zliczmy, dla każdego
gdyż tylko takie numery będą w ostatecznym ponumerowaniu. Zliczmy, dla każdego 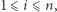 liczbę klocków z numerem
liczbę klocków z numerem 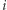 (niech
(niech 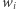 oznacza tę wartość). Teraz problem możemy opisać następująco. Mamy
oznacza tę wartość). Teraz problem możemy opisać następująco. Mamy 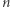 numerów, a
numerów, a 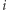 -ty numer ma wartość
-ty numer ma wartość 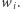 Intuicyjnie, wartość numeru oznacza, ile już klocków z tym numerem mamy. Naszym celem jest wybrać najbardziej wartościowy podzbiór numerów sumujących się do
Intuicyjnie, wartość numeru oznacza, ile już klocków z tym numerem mamy. Naszym celem jest wybrać najbardziej wartościowy podzbiór numerów sumujących się do 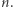 Wówczas liczba klocków, które należy przenumerować, to
Wówczas liczba klocków, które należy przenumerować, to 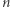 pomniejszone o znalezioną wartość podzbioru.
pomniejszone o znalezioną wartość podzbioru.
Otrzymany problem jest podobny do problemu plecakowego (numery są przedmiotami). Z jedną różnicą, chcemy zapełnić plecak "po brzegi", tzn. wybrać podzbiór, którego numery sumują się do 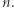 Opiszemy teraz, w jaki sposób znaleźć taki podzbiór.
Opiszemy teraz, w jaki sposób znaleźć taki podzbiór.
Niech ![|T[ j],](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/1x-3264ef97fcab5a73c70d4d28af134a0741deca88-im-33,33,33-FF,FF,FF.gif) dla
dla 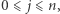 oznacza wartość najbardziej wartościowego podzbioru o sumie numerów równej
oznacza wartość najbardziej wartościowego podzbioru o sumie numerów równej 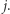 Początkowo
Początkowo ![|T[0] = 0](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/4x-3264ef97fcab5a73c70d4d28af134a0741deca88-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![|T[ j] = −∞](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/5x-3264ef97fcab5a73c70d4d28af134a0741deca88-im-33,33,33-FF,FF,FF.gif) dla
dla 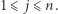 Następnie przeglądamy kolejne numery, które mogą tworzyć finalny podzbiór (numery od
Następnie przeglądamy kolejne numery, które mogą tworzyć finalny podzbiór (numery od 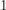 do
do 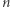 ). Załóżmy, że rozpatrujemy numer
). Załóżmy, że rozpatrujemy numer 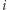 o wartości
o wartości 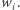 Chcemy policzyć nowe wartości tablicy
Chcemy policzyć nowe wartości tablicy 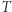 (z uwzględnionym
(z uwzględnionym 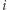 -tym numerem), oznaczmy te wartości przez
-tym numerem), oznaczmy te wartości przez 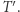 Wówczas:
Wówczas:
![T ′[ j] = max(T [ j],T [ j− i]+ w ) jeś liT j−i ~−∞](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/14x-3264ef97fcab5a73c70d4d28af134a0741deca88-dm-33,33,33-FF,FF,FF.gif)
( ![T[ j]](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/15x-3264ef97fcab5a73c70d4d28af134a0741deca88-im-33,33,33-FF,FF,FF.gif) oznacza przypadek, kiedy do podzbioru o sumie
oznacza przypadek, kiedy do podzbioru o sumie 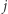 nie bierzemy
nie bierzemy 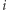 -tego oraz wyższych numerów, zaś
-tego oraz wyższych numerów, zaś ![T [ j− i]+ w](/math/temat/informatyka/algorytmy/2019/03/28/Klocki_z_numerami_i_pileczki/18x-3264ef97fcab5a73c70d4d28af134a0741deca88-im-33,33,33-FF,FF,FF.gif) oznacza przypadek, kiedy
oznacza przypadek, kiedy 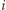 -ty numer włączamy do podzbioru). Po obliczeniu
-ty numer włączamy do podzbioru). Po obliczeniu 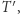 przepisujemy wartości
przepisujemy wartości 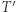 do
do 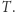
Dla każdego z 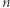 przedmiotów przeglądamy
przedmiotów przeglądamy 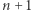 elementową tablicę
elementową tablicę 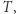 zatem otrzymujemy rozwiązanie w złożoności czasowej
zatem otrzymujemy rozwiązanie w złożoności czasowej 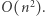
Zadanie (Piłeczki na podłodze). Danych jest 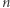 punktów na płaszczyźnie, ponumerowanych od
punktów na płaszczyźnie, ponumerowanych od 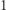 do
do 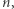
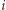 -ty punkt ma współrzędne
-ty punkt ma współrzędne 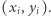 Naszym zadaniem jest pokolorować te punkty (każdy punkt na czerwono albo niebiesko). Chcemy, aby odległość pomiędzy najbliższymi dwoma punktami w tym samym kolorze była jak największa.
Naszym zadaniem jest pokolorować te punkty (każdy punkt na czerwono albo niebiesko). Chcemy, aby odległość pomiędzy najbliższymi dwoma punktami w tym samym kolorze była jak największa.
Rozwiązanie 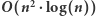
Stwórzmy graf pełny 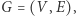 gdzie:
gdzie:
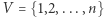 - zbiór
- zbiór  wierzchołków,
wierzchołków,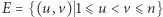 - zbiór
- zbiór 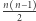 krawędzi nieskierowanych.
krawędzi nieskierowanych.
Niech 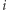 -temu punktowi odpowiada
-temu punktowi odpowiada 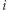 -ty wierzchołek. Wagą krawędzi
-ty wierzchołek. Wagą krawędzi 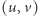 niech będzie kwadrat odległości pomiędzy
niech będzie kwadrat odległości pomiędzy  -tym i
-tym i  -tym wierzchołkiem, tj.
-tym wierzchołkiem, tj. 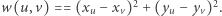 Na potrzeby tego rozwiązania wprowadźmy nowe pojęcie:
Na potrzeby tego rozwiązania wprowadźmy nowe pojęcie: 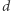 -porządek, czyli takie przyporządkowanie kolorów wierzchołkom, że waga krawędzi pomiędzy dowolnymi dwoma wierzchołkami w tym samym kolorze wynosi przynajmniej
-porządek, czyli takie przyporządkowanie kolorów wierzchołkom, że waga krawędzi pomiędzy dowolnymi dwoma wierzchołkami w tym samym kolorze wynosi przynajmniej 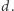 Naszym zadaniem jest znaleźć takie największe
Naszym zadaniem jest znaleźć takie największe 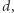 dla którego istnieje
dla którego istnieje 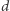 -porządek.
-porządek.
Zauważmy, że 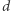 -porządek jest również
-porządek jest również 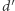 -porządkiem dla
-porządkiem dla 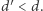 Zatem wartość
Zatem wartość 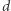 możemy znaleźć za pomocą wyszukiwania binarnego. Pozostało nam więc opisać algorytm, który dla ustalonego
możemy znaleźć za pomocą wyszukiwania binarnego. Pozostało nam więc opisać algorytm, który dla ustalonego 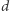 sprawdzi, czy istnieje
sprawdzi, czy istnieje 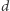 -porządek. Zbudujmy graf
-porządek. Zbudujmy graf 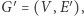 gdzie
gdzie 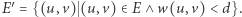 Otrzymaliśmy graf
Otrzymaliśmy graf 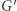 z grafu
z grafu 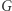 poprzez usunięcie krawędzi o wadze większej lub równej
poprzez usunięcie krawędzi o wadze większej lub równej 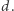 Nie musimy uwzględniać tych krawędzi, ponieważ ich końce mogą być pokolorowane na ten sam kolor.
Nie musimy uwzględniać tych krawędzi, ponieważ ich końce mogą być pokolorowane na ten sam kolor. 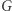 będzie
będzie 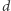 -porządkiem, jeśli
-porządkiem, jeśli 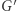 będzie grafem dwudzielnym. Aby sprawdzić, czy
będzie grafem dwudzielnym. Aby sprawdzić, czy 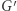 jest dwudzielny, należy sprawdzić, czy każda spójna tego grafu jest dwudzielna. Sprawdzenie, czy spójna jest dwudzielna, rozpoczynamy od wybrania dowolnego wierzchołka i pokolorowania go na czerwono. Następnie przeszukujemy graf (np. za pomocą algorytmu DFS) i odwiedzanym wierzchołkom przypisujemy kolor przeciwny do koloru poprzednika. Jeśli natrafimy na krawędź, która łączy dwa wierzchołki z przyporządkowanym tym samym kolorem, to wiemy, że graf nie jest dwudzielny. Jeśli natomiast nie wystąpi żadna kolizja, to znaczy, że graf jest dwudzielny.
jest dwudzielny, należy sprawdzić, czy każda spójna tego grafu jest dwudzielna. Sprawdzenie, czy spójna jest dwudzielna, rozpoczynamy od wybrania dowolnego wierzchołka i pokolorowania go na czerwono. Następnie przeszukujemy graf (np. za pomocą algorytmu DFS) i odwiedzanym wierzchołkom przypisujemy kolor przeciwny do koloru poprzednika. Jeśli natrafimy na krawędź, która łączy dwa wierzchołki z przyporządkowanym tym samym kolorem, to wiemy, że graf nie jest dwudzielny. Jeśli natomiast nie wystąpi żadna kolizja, to znaczy, że graf jest dwudzielny.
Liczba krawędzi w 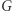 jest rzędu
jest rzędu 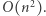 Zatem algorytm wyszukiwania binarnego wykona
Zatem algorytm wyszukiwania binarnego wykona 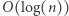 faz. W każdej fazie budujemy graf rozmiaru
faz. W każdej fazie budujemy graf rozmiaru 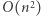 i w czasie liniowym od jego rozmiaru sprawdzamy, czy graf jest dwudzielny. Całkowita złożoność czasowa to
i w czasie liniowym od jego rozmiaru sprawdzamy, czy graf jest dwudzielny. Całkowita złożoność czasowa to