Informatyczny kącik olimpijski
Liczby prawie pół-pierwsze
Tym razem omówimy zadanie Liczby prawie pół-pierwsze, które pojawiło się na Sobotnim Kole Naukowym (25.11.2017) organizowanym przez Stowarzyszenie Talent w III Liceum Ogólnokształcącym w Gdyni.
Definicja. Liczbę 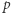 nazywamy prawie pół-pierwszą, jeśli jest iloczynem dwóch liczb pierwszych
nazywamy prawie pół-pierwszą, jeśli jest iloczynem dwóch liczb pierwszych 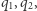 gdzie
gdzie 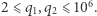 Liczby
Liczby 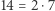 i
i 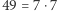 są prawie pół-pierwsze. Natomiast liczby
są prawie pół-pierwsze. Natomiast liczby 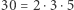 i
i 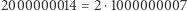 nie są prawie pół-pierwsze.
nie są prawie pół-pierwsze.
Zadanie. Dane są dwie liczby całkowite  i
i 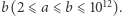 Oblicz, ile jest liczb prawie pół-pierwszych na przedziale
Oblicz, ile jest liczb prawie pół-pierwszych na przedziale ![[a,b].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/10x-d59908a1edbc3824d6b9db25e9bed2bcccce6a49-im-33,33,33-FF,FF,FF.gif)
Rozwiązanie 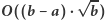
Pierwszy pomysł, który nasuwa się po przeczytaniu treści, polega na przejrzeniu wszystkich liczb całkowitych z przedziału ![[a,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-b72bdd5f2ed47bbd28cc182f1bb81322c1c653ec-im-33,33,33-FF,FF,FF.gif) i zliczeniu tych, które są prawie pół-pierwsze. Liczba prawie pół-pierwsza zawiera dokładnie dwie liczby pierwsze nie większe niż
i zliczeniu tych, które są prawie pół-pierwsze. Liczba prawie pół-pierwsza zawiera dokładnie dwie liczby pierwsze nie większe niż 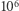 w rozkładzie na czynniki pierwsze. Rozkład na czynniki pierwsze liczby całkowitej
w rozkładzie na czynniki pierwsze. Rozkład na czynniki pierwsze liczby całkowitej 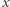 możemy znaleźć w czasie
możemy znaleźć w czasie 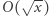 (przeglądamy potencjalne dzielniki pierwsze z przedziału
(przeglądamy potencjalne dzielniki pierwsze z przedziału ![|[2,⌈√ x-⌉]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/6x-b72bdd5f2ed47bbd28cc182f1bb81322c1c653ec-im-33,33,33-FF,FF,FF.gif) ). Rozwiązanie działa w czasie
). Rozwiązanie działa w czasie 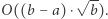
Rozwiązanie 
W tym podejściu, podobnie jak wcześniej, dla każdej liczby całkowitej z przedziału ![|[a,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-38e42755c95b264331de62d6b6b4495590f0a30b-im-33,33,33-FF,FF,FF.gif) sprawdzimy, czy jest ona prawie pół-pierwsza.
sprawdzimy, czy jest ona prawie pół-pierwsza.
Zacznijmy od stworzenia takiej tablicy 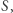 że
że ![S[i]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif) dla każdego
dla każdego ![|i∈[2,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/3x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif) oznacza najmniejszy dzielnik pierwszy
oznacza najmniejszy dzielnik pierwszy 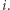 W tym celu wystarczy nieznacznie zmodyfikować sito Eratostenesa. Zamiast zapamiętywać informację, czy liczba jest pierwsza czy złożona, będziemy pamiętali jej najmniejszy dzielnik, będący liczbą pierwszą. Strukturę budujemy w czasie
W tym celu wystarczy nieznacznie zmodyfikować sito Eratostenesa. Zamiast zapamiętywać informację, czy liczba jest pierwsza czy złożona, będziemy pamiętali jej najmniejszy dzielnik, będący liczbą pierwszą. Strukturę budujemy w czasie 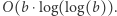 Wówczas w czasie stałym możemy stwierdzić, że:
Wówczas w czasie stałym możemy stwierdzić, że:
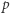 jest pierwsze, jeśli:
jest pierwsze, jeśli: ![|S[p] = p,](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/8x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif)
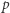 jest prawie pół-pierwsze, jeśli:
jest prawie pół-pierwsze, jeśli: ![-p- -p- -p- 6 S[p] /= p ∧S[ S p ] == S p ∧ S[p],S p ⩽ 10 .](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/11x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif)
Wtedy jej dzielnikami pierwszymi są![S[p]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/12x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif) i
i 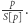
Po wygenerowaniu 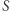 zliczamy liczby prawie pół-pierwsze z przedziału
zliczamy liczby prawie pół-pierwsze z przedziału ![|[a, b].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/15x-91481d314b6424f1321da2d5ef5e9359e8803c8a-im-33,33,33-FF,FF,FF.gif) Rozwiązanie działa w czasie
Rozwiązanie działa w czasie 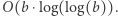
Rozwiązanie 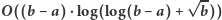
Niech 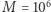 oraz
oraz ![|T[i]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/3x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) dla każdego
dla każdego ![] |i∈ [2,M](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/4x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) wskazuje, czy
wskazuje, czy 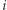 jest pierwsze
jest pierwsze ![(T [i] = 1),](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/6x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) czy złożone
czy złożone ![|(T[i] = 0).](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/7x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) Dla pozostałych
Dla pozostałych 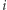 niech
niech ![|T[i] = 0.](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/9x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif)
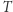 obliczamy za pomocą sita Eratostenesa. Dodatkowo stwórzmy taką tablicę
obliczamy za pomocą sita Eratostenesa. Dodatkowo stwórzmy taką tablicę 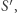 że
że ![′ S [i]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/12x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) dla każdego
dla każdego ![i ∈[a,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/13x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) będzie oznaczało najmniejszy dzielnik pierwszy
będzie oznaczało najmniejszy dzielnik pierwszy 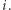 Konstrukcja
Konstrukcja 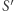 jest następująca. Najpierw przypisujemy
jest następująca. Najpierw przypisujemy ![S ′[i] = i](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/16x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) dla każdego
dla każdego ![|i∈ [a,b].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/17x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) Następnie dla każdej liczby pierwszej
Następnie dla każdej liczby pierwszej ![|q∈ [2,⌈√ b⌉]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/18x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) przeglądamy jej wielokrotności w przedziale
przeglądamy jej wielokrotności w przedziale ![|[a, b],](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/19x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) czyli liczby
czyli liczby 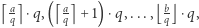 i aktualizujemy ich najmniejszy dzielnik pierwszy. Zauważmy, że wielokrotności
i aktualizujemy ich najmniejszy dzielnik pierwszy. Zauważmy, że wielokrotności 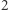 w przedziale
w przedziale ![|[a,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/22x-bc6441ebc3be97f1eebbd901afca163145928e8a-im-33,33,33-FF,FF,FF.gif) jest co najwyżej
jest co najwyżej 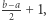 wielokrotności
wielokrotności 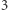 jest co najwyżej
jest co najwyżej 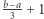 itd. Zatem konstrukcja struktury zajmuje
itd. Zatem konstrukcja struktury zajmuje 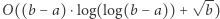 operacji.
operacji.
Na koniec zliczamy liczby prawie pół-pierwsze z przedziału ![|[a, b],](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/1x-7fab6cd205c1098a7e4dd0501dc289342802ec3e-im-33,33,33-FF,FF,FF.gif) czyli takie
czyli takie ![|p∈ [a,b],](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-7fab6cd205c1098a7e4dd0501dc289342802ec3e-im-33,33,33-FF,FF,FF.gif) że:
że:
![p ′ ′ ∧T[′]=1 S[p] /= p∧ S [p] ⩽M . S[p]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/3x-7fab6cd205c1098a7e4dd0501dc289342802ec3e-dm-33,33,33-FF,FF,FF.gif)
Rozwiązanie 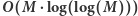
Niech 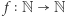 będzie taką funkcją, że
będzie taką funkcją, że 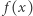 oznacza liczbę liczb prawie pół-pierwszych na przedziale
oznacza liczbę liczb prawie pół-pierwszych na przedziale ![|[1,x].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/7x-7fab6cd205c1098a7e4dd0501dc289342802ec3e-im-33,33,33-FF,FF,FF.gif) Wówczas liczb prawie pół-pierwszych na przedziale
Wówczas liczb prawie pół-pierwszych na przedziale ![[a,b]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/8x-7fab6cd205c1098a7e4dd0501dc289342802ec3e-im-33,33,33-FF,FF,FF.gif) jest
jest 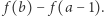
Opiszemy teraz, jak policzyć 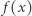 dla
dla ![|x ∈[1,1012].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-8dbeb18fd8d95900fc0e463e94d28553a06b37f0-im-33,33,33-FF,FF,FF.gif) Zacznijmy od wygenerowania ciągu kolejnych liczb pierwszych nie większych niż
Zacznijmy od wygenerowania ciągu kolejnych liczb pierwszych nie większych niż 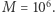 Oznaczmy ten ciąg jako
Oznaczmy ten ciąg jako 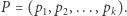 Początkowymi wyrazami ciągu są:
Początkowymi wyrazami ciągu są: 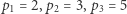 itd. Liczby pierwsze możemy znaleźć za pomocą sita Eratostenesa. Zauważmy, że tylko elementy ciągu
itd. Liczby pierwsze możemy znaleźć za pomocą sita Eratostenesa. Zauważmy, że tylko elementy ciągu 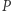 mogą występować w rozkładzie na czynniki pierwsze liczb prawie pół-pierwszych. Zatem:
mogą występować w rozkładzie na czynniki pierwsze liczb prawie pół-pierwszych. Zatem:

Wartość 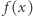 możemy policzyć naiwnie, przeglądając wszystkie pary elementów ciągu
możemy policzyć naiwnie, przeglądając wszystkie pary elementów ciągu 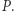 Niestety takie rozwiązanie jest wolne, ponieważ przegląda się
Niestety takie rozwiązanie jest wolne, ponieważ przegląda się 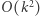 par elementów, gdzie
par elementów, gdzie 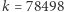 (tyle jest liczb pierwszych nie większych niż
(tyle jest liczb pierwszych nie większych niż 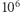 ).
).
Na szczęście możemy to przyspieszyć. Niektóre pary będziemy zliczali "hurtowo". Dokładniej, dla każdego ![i∈ [1,k]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/1x-fc7137dc55589c14747341ee9ac3afb45a7ae1a2-im-33,33,33-FF,FF,FF.gif) wyznaczymy takie największe
wyznaczymy takie największe ![| ji∈ [i,k],](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/2x-fc7137dc55589c14747341ee9ac3afb45a7ae1a2-im-33,33,33-FF,FF,FF.gif) że
że 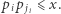 Jeśli takie
Jeśli takie 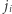 nie istnieje, to niech
nie istnieje, to niech 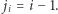 Wówczas liczby postaci
Wówczas liczby postaci 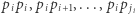 są prawie pół-pierwsze. Zaś wszystkich par jest
są prawie pół-pierwsze. Zaś wszystkich par jest 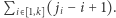 Algorytm przebiega następująco. Najpierw naiwnie znajdujemy
Algorytm przebiega następująco. Najpierw naiwnie znajdujemy 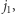 przeglądając przedział indeksów
przeglądając przedział indeksów ![| [1,k].](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/9x-fc7137dc55589c14747341ee9ac3afb45a7ae1a2-im-33,33,33-FF,FF,FF.gif) Następnie kolejno wyznaczamy wartości
Następnie kolejno wyznaczamy wartości 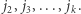
Obserwacja: Dla każdego ![| i ∈[2,k]](/math/temat/informatyka/algorytmy/2019/02/28/Liczby_prawie_pol-pierwsze/1x-59ded99ee426da38da528accff6277a4272f4c12-im-33,33,33-FF,FF,FF.gif) zachodzi
zachodzi 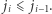
Dowód: Wiemy, że 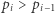 oraz
oraz 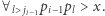 Stąd
Stąd 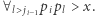 Zatem
Zatem 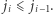
Na mocy powyższej obserwacji, szukanie wartości 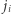 możemy rozpocząć od
możemy rozpocząć od 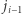 i zmniejszać ją dopóki
i zmniejszać ją dopóki 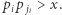 W ten sposób wykonamy
W ten sposób wykonamy 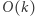 operacji podczas obliczania
operacji podczas obliczania 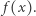 Całe rozwiązanie działa w czasie
Całe rozwiązanie działa w czasie