Informatyczny kącik olimpijski
Wyspa i liczydło
Tym razem omówimy dwa zadania: Wyspę z IX OIG oraz Liczydło z XII OIG.
Zadanie (Wyspa). Dany jest prostokąt o bokach równoległych do osi układu współrzędnych, którego lewy-dolny róg ma współrzędne 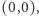 zaś prawy-górny róg ma współrzędne
zaś prawy-górny róg ma współrzędne 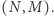 Dla podanego
Dla podanego 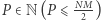 chcemy znaleźć taki czworokąt wypukły o polu
chcemy znaleźć taki czworokąt wypukły o polu 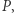 którego wierzchołki mają współrzędne całkowite oraz należą do prostokąta.
którego wierzchołki mają współrzędne całkowite oraz należą do prostokąta.
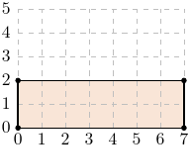
Rys. 1
Przypadek: 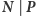
Rozważmy najpierw przypadek, kiedy 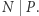 Wtedy możemy zbudować prostokąt, którego wierzchołkami są:
Wtedy możemy zbudować prostokąt, którego wierzchołkami są: 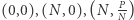 i
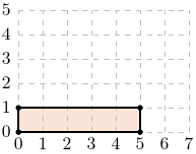
i 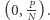 Przykład dla:
Przykład dla: 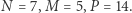 [Rys. 1]
[Rys. 1]
Przypadek: 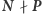
Ten przypadek przeanalizujemy w trzech krokach:
- (1)
- Jeśli
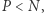 wtedy możemy zbudować prostokąt, którego wierzchołkami są:
wtedy możemy zbudować prostokąt, którego wierzchołkami są: 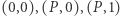 i
i 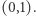 Przykład dla:
Przykład dla: 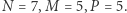 [Rys. 2]
[Rys. 2] - (2)
- Jeśli
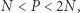 wtedy możemy zbudować trapez, którego wierzchołkami są:
wtedy możemy zbudować trapez, którego wierzchołkami są: 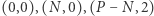 i
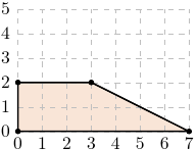
i 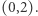 Przykład dla:
Przykład dla: 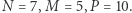 [Rys. 3]
[Rys. 3] - (3)
- Został nam do rozpatrzenia przypadek, kiedy
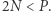 Niech:
Niech:
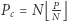 (największa wielokrotność
(największa wielokrotność 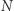 nie większa niż
nie większa niż 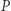 ),
),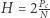 (wysokość trójkąta o podstawie
(wysokość trójkąta o podstawie 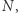 który ma pole
który ma pole 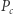 ),
),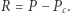 Wówczas możemy zbudować czworokąt, którego wierzchołkami są:
Wówczas możemy zbudować czworokąt, którego wierzchołkami są: 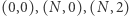 i
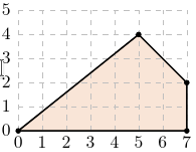
i 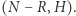 Przykład dla:
Przykład dla: 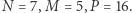 Wtedy
Wtedy 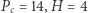 oraz
oraz 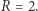 [Rys. 4]
[Rys. 4]
Powyższe rozważania pokrywają wszystkie przypadki. Dla każdego z nich udało nam się wskazać czworokąt wypukły o polu 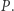
Zadanie (Liczydło). Dane są dwie liczby całkowite 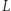 i
i 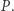 W każdym kroku możemy wykonać jedną z dwóch operacji: 1) dodać dowolnie wybraną liczbę całkowitą do
W każdym kroku możemy wykonać jedną z dwóch operacji: 1) dodać dowolnie wybraną liczbę całkowitą do 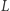 oraz do
oraz do 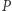 (jednocześnie); 2) przemnożyć L lub P przez dowolnie wybraną niezerową liczbę całkowitą. Ile minimalnie operacji należy wykonać, aby obie liczby stały się równe zero?
(jednocześnie); 2) przemnożyć L lub P przez dowolnie wybraną niezerową liczbę całkowitą. Ile minimalnie operacji należy wykonać, aby obie liczby stały się równe zero?
Zauważmy najpierw, że tylko dla 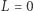 i
i 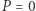 odpowiedzią jest
odpowiedzią jest 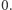 Podobnie, tylko dla
Podobnie, tylko dla 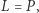 gdzie
gdzie 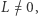 odpowiedzią jest
odpowiedzią jest 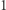 - wystarczy do obu liczb dodać
- wystarczy do obu liczb dodać 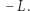
W pozostałych przypadkach odpowiedź będzie większa od 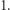 Zauważmy, że operacja typu
Zauważmy, że operacja typu 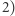 nie pozwala wyzerować niezerowej liczby, więc ostatnia operacja będzie typu
nie pozwala wyzerować niezerowej liczby, więc ostatnia operacja będzie typu 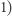 i zostanie zastosowana do dwóch równych liczb. Jak zatem wyrównać dwie liczby w minimalnej liczbie ruchów?
i zostanie zastosowana do dwóch równych liczb. Jak zatem wyrównać dwie liczby w minimalnej liczbie ruchów?
Rozważmy przypadek, kiedy jedna z liczb jest wielokrotnością drugiej (bez straty ogólności załóżmy, że 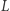 jest wielokrotnością
jest wielokrotnością 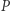 ):
):
- jeśli
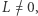 wtedy
wtedy 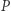 mnożymy przez
mnożymy przez 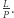 Całkowita liczba operacji wynosi
Całkowita liczba operacji wynosi 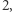
- jeśli
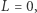 wtedy do obu liczb dodajemy
wtedy do obu liczb dodajemy 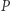 i tę o mniejszej wartości bezwzględnej mnożymy przez
i tę o mniejszej wartości bezwzględnej mnożymy przez 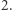 Całkowita liczba operacji wynosi
Całkowita liczba operacji wynosi 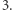
Pozostał nam ostatni przypadek, kiedy 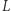 nie jest wielokrotnością
nie jest wielokrotnością 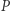 oraz
oraz 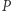 nie jest wielokrotnością
nie jest wielokrotnością 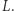 Wtedy mnożymy
Wtedy mnożymy 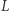 przez
przez 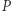 oraz
oraz 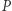 przez
przez 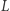 i otrzymujemy dwie równe liczby. Wówczas odpowiedzią jest
i otrzymujemy dwie równe liczby. Wówczas odpowiedzią jest 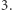
Prosty dowód, że w każdym z powyższych przypadków korzystamy z minimalnej liczby operacji, pozostawiamy Czytelnikowi.