Problem izomorfizmu grafów
Spójrzmy na dwa grafy na poniższym rysunku. Wyglądają zupełnie inaczej, prawda?
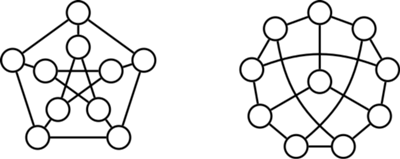
A jednak to tylko złudzenie. Tak naprawdę to jest ten sam graf, ale inaczej narysowany. Istotnie, poniżej ponumerowaliśmy wierzchołki obu grafów od 0 do 9 i łatwo można sprawdzić, że w obu przypadkach wierzchołek o danym numerze ma takie same numery sąsiadów.
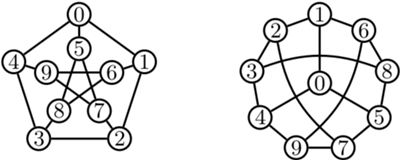
Izomorfizm grafów 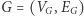 i
i 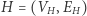 to dowolna bijekcja
to dowolna bijekcja 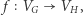 taka że dowolne dwa wierzchołki
taka że dowolne dwa wierzchołki 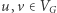 sąsiadują w
sąsiadują w 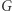 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 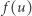 i
i 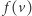 sąsiadują w
sąsiadują w 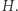 Gdy izomorfizm z
Gdy izomorfizm z 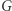 do
do 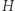 istnieje, mówimy, że grafy
istnieje, mówimy, że grafy 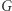 i
i 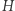 są izomorficzne. Przykład izomorfizmu grafów widzimy na rysunku powyżej.
są izomorficzne. Przykład izomorfizmu grafów widzimy na rysunku powyżej.
Informatyk od razu zapyta o algorytm rozstrzygający, czy dane dwa grafy są izomorficzne. Oznaczmy 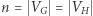 (gdy ostatnia równość nie zachodzi, problem jest banalny). Algorytm wynikający wprost z definicji sprawdza wszystkie
(gdy ostatnia równość nie zachodzi, problem jest banalny). Algorytm wynikający wprost z definicji sprawdza wszystkie 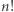 bijekcji i działa w czasie
bijekcji i działa w czasie 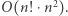 Ale czy istnieje algorytm wielomianowy? To niewinne pytanie jest jednym z największych problemów otwartych współczesnej informatyki.
Ale czy istnieje algorytm wielomianowy? To niewinne pytanie jest jednym z największych problemów otwartych współczesnej informatyki.
Oczytany Czytelnik zapewne zna wiele innych problemów grafowych, dla których algorytm wielomianowy nie jest znany: problem kliki, problem cyklu Hamiltona, problem kolorowania. Są to problemy NP-zupełne, a rozwiązanie jednego z nich w czasie wielomianowym od razu implikuje takie rozwiązanie dla pozostałych (oraz tysięcy innych nazwanych problemów z klasy NP). Co ciekawe, nie wiemy, czy problem izomorfizmu grafów jest NP-zupełny! Mamy nawet istotne powody, aby podejrzewać, że tak nie jest (przeczyłoby to kilku znanym hipotezom). Gdy autor tego artykułu był studentem, znany był jeszcze jeden problem o podobnym statusie: testowanie pierwszości liczb, w 2002 roku został on jednak rozwiązany w czasie wielomianowym. Czy ten sam los czeka izomorfizm grafów? Aktualny rekord świata, który ustanowił Laszlo Babai dwa lata temu, to algorytm działający w czasie 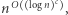 dla pewnej stałej
dla pewnej stałej 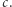
Zanim porwiemy się na trudny problem, warto zrozumieć jego szczególne, być może prostsze, przypadki. Jedną z najprostszych klas grafów są drzewa (grafy spójne bez cykli). Jak sprawdzić, czy dwa drzewa, 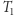 i
i 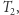 są izomorficzne? Niech
są izomorficzne? Niech  będzie dowolnym wierzchołkiem
będzie dowolnym wierzchołkiem 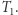 Rozpatrzmy wszystkie
Rozpatrzmy wszystkie  możliwości ustalenia
możliwości ustalenia 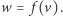 Możemy ukorzenić
Możemy ukorzenić 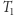 w
w 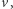 tzn. uznać, że
tzn. uznać, że  jest korzeniem, a dla dowolnego innego wierzchołka
jest korzeniem, a dla dowolnego innego wierzchołka 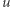 sąsiad
sąsiad 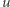 na (jedynej) ścieżce do
na (jedynej) ścieżce do  jest ojcem
jest ojcem 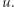 Podobnie ukorzeniamy
Podobnie ukorzeniamy 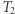 w
w  Naszym celem będzie przypisanie każdemu ukorzenionemu drzewu identyfikatora (wyrażenia nawiasowego) tak, aby drzewa były izomorficzne wtedy i tylko wtedy, gdy mają te same identyfikatory. Wówczas wystarczy porównać identyfikatory
Naszym celem będzie przypisanie każdemu ukorzenionemu drzewu identyfikatora (wyrażenia nawiasowego) tak, aby drzewa były izomorficzne wtedy i tylko wtedy, gdy mają te same identyfikatory. Wówczas wystarczy porównać identyfikatory 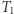 i
i 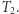 Drzewo składające się z pojedynczego wierzchołka dostaje identyfikator ().
Drzewo składające się z pojedynczego wierzchołka dostaje identyfikator ().
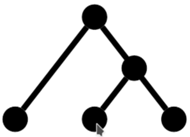
Powyższe drzewo zakodujemy jako ((()())()), zakładając, że w naszym porządku sortowania nawias otwierający poprzedza nawias zamykający.
Identyfikator drzewa powstaje przez a) posortowanie identyfikatorów poddrzew korzenia, b) sklejanie ich w uzyskanej w kolejności w jedno słowo, c) dodanie symbolu ( na początku i symbolu ) na końcu. Czytelnik Pracowity na pewno z łatwością wykaże przez indukcję, że istotnie tylko izomorficzne drzewa dają ten sam identyfikator dla pewnej wartości 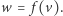 Tak uzyskany algorytm jest wielomianowy, a kosztem dodatkowego wysiłku można tę złożoność zmniejszyć nawet do liniowej.
Tak uzyskany algorytm jest wielomianowy, a kosztem dodatkowego wysiłku można tę złożoność zmniejszyć nawet do liniowej.
Istnieją znacznie bardziej złożone klasy grafów niż drzewa, dla których problem izomorfizmu grafów ma wielomianowe rozwiązanie. Jedną z nich są grafy planarne, tzn. takie, które można narysować na płaszczyźnie bez przecięć krawędzi. Algorytm opiera się na twierdzeniu Whitneya, mówiącemu, że jeśli graf planarny jest 3-spójny (nie da się usunąć dwóch wierzchołków tak, aby uzyskać graf, który nie jest spójny), to można go narysować na sferze w jeden tylko sposób. Dokładniej, każdy rysunek można przekształcić w inny za pomocą ciągłego odwzorowania sfery w sferę. Takie odwzorowania nie zmieniają np. cyklicznej kolejności sąsiadów wierzchołka, a więc gdy mamy już na sferze narysowane dwa grafy i zgadniemy, jak izomorfizm odwzorowuje wierzchołki dowolnej wybranej krawędzi 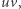 to pozostałe wartości izomorfizmu są wyznaczone jednoznacznie (najpierw wyznaczymy obrazy sąsiadów
to pozostałe wartości izomorfizmu są wyznaczone jednoznacznie (najpierw wyznaczymy obrazy sąsiadów 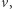 potem sąsiadów sąsiadów
potem sąsiadów sąsiadów 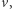 itd.). Graf ma rysunek na sferze wtedy i tylko wtedy, gdy jest planarny, a przejście od 3-spójnych grafów planarnych do dowolnych planarnych nie jest trudne. Inny słynny wynik to grafy o stopniu ograniczonym przez stałą
itd.). Graf ma rysunek na sferze wtedy i tylko wtedy, gdy jest planarny, a przejście od 3-spójnych grafów planarnych do dowolnych planarnych nie jest trudne. Inny słynny wynik to grafy o stopniu ograniczonym przez stałą 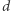 : w 1983 roku Babai i Luks podali algorytm działający w czasie
: w 1983 roku Babai i Luks podali algorytm działający w czasie 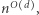 korzystając z zaawansowanych narzędzi teorii grup.
korzystając z zaawansowanych narzędzi teorii grup.
Na szczęście w praktyce jest dużo lepiej niż w teorii. Rozważmy następujący algorytm. Na początku wszystkie wierzchołki 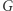 i
i 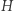 otrzymują ten sam kolor. Niech
otrzymują ten sam kolor. Niech 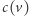 oznacza kolor
oznacza kolor  Następnie dla każdego wierzchołka
Następnie dla każdego wierzchołka  tworzymy multizbiór (tj. zbiór z powtórzeniami) kolorów jego sąsiadów
tworzymy multizbiór (tj. zbiór z powtórzeniami) kolorów jego sąsiadów 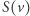 i zapamiętujemy parę
i zapamiętujemy parę 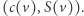 Pokolorujemy teraz graf na nowo w ten sposób, by dwa wierzchołki miały ten sam kolor tylko wtedy, gdy utworzyły wcześniej tę samą parę
Pokolorujemy teraz graf na nowo w ten sposób, by dwa wierzchołki miały ten sam kolor tylko wtedy, gdy utworzyły wcześniej tę samą parę 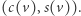 Postępujemy w ten sposób tak długo, dopóki zwiększa się liczba kolorów. Jeśli multizbiory kolorów wierzchołków
Postępujemy w ten sposób tak długo, dopóki zwiększa się liczba kolorów. Jeśli multizbiory kolorów wierzchołków 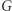 i
i 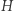 są inne, mamy pewność, że
są inne, mamy pewność, że 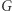 i
i 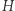 nie są izomorficzne (dlaczego?). Zauważmy, że już po pierwszym kroku algorytm ten rozróżni grafy o innych posortowanych ciągach stopni wierzchołków. Łatwo wykazać, że poprawnie rozróżnia on drzewa. Z drugiej strony, nie rozróżnia grafów regularnych. Okazuje się jednak, że można ten pomysł uogólnić, kolorując wszystkie ciągi
nie są izomorficzne (dlaczego?). Zauważmy, że już po pierwszym kroku algorytm ten rozróżni grafy o innych posortowanych ciągach stopni wierzchołków. Łatwo wykazać, że poprawnie rozróżnia on drzewa. Z drugiej strony, nie rozróżnia grafów regularnych. Okazuje się jednak, że można ten pomysł uogólnić, kolorując wszystkie ciągi 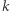 wierzchołków. Jest to algorytm Weisfeilera-Lehmana wymiaru
wierzchołków. Jest to algorytm Weisfeilera-Lehmana wymiaru 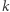 i świetnie sprawdza się w praktyce. Już wymiar
i świetnie sprawdza się w praktyce. Już wymiar 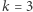 wystarcza, aby rozróżnić grafy planarne. Niestety, okazuje się, że aby rozróżnić dowolne grafy w pesymistycznym przypadku potrzeba wymiaru co najmniej liniowego od
wystarcza, aby rozróżnić grafy planarne. Niestety, okazuje się, że aby rozróżnić dowolne grafy w pesymistycznym przypadku potrzeba wymiaru co najmniej liniowego od 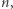 a więc nie tędy droga do rozwiązania naszego problemu otwartego. Na szczęście pesymistyczne przypadki zdarzają się niezwykle rzadko w rzeczywistych danych.
a więc nie tędy droga do rozwiązania naszego problemu otwartego. Na szczęście pesymistyczne przypadki zdarzają się niezwykle rzadko w rzeczywistych danych.