Mnożenie nie tylko macierzy
Tematem tego artykułu jest mnożenie macierzy, ale zaczniemy od problemu nieco prostszego - mnożenia wielomianów...
Niech 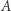 i
i 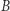 będą wielomianami stopnia
będą wielomianami stopnia 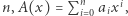
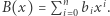 Iloczynem
Iloczynem 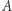 i
i 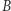 jest wielomian
jest wielomian 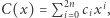 gdzie
gdzie 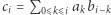 (przyjmujemy
(przyjmujemy 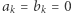 dla
dla 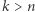 ).
).
Mnożenie wielomianów za pomocą tego wzoru wymaga rzędu 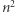 operacji. Okazuje się jednak, że można to zrobić szybciej. Jako pierwszy zauważył to Anatolij Karatsuba już w 1960 roku. Algorytm Karatsuby opiera się na następującym spostrzeżeniu. Rozważmy iloczyn wielomianów szczególnie prostej postaci:
operacji. Okazuje się jednak, że można to zrobić szybciej. Jako pierwszy zauważył to Anatolij Karatsuba już w 1960 roku. Algorytm Karatsuby opiera się na następującym spostrzeżeniu. Rozważmy iloczyn wielomianów szczególnie prostej postaci:

Wydaje się, że do obliczenia współczynników wyniku potrzebne są cztery mnożenia, ale wystarczą trzy, gdyż

W ogólnym przypadku, aby pomnożyć dwa wielomiany 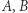 stopnia
stopnia 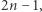 zapisujemy
zapisujemy 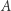 następująco:
następująco:

i analogicznie 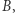 a następnie korzystamy z wyprowadzonej właśnie tożsamości. Sprowadzamy w ten sposób jedno mnożenie wielomianów stopnia
a następnie korzystamy z wyprowadzonej właśnie tożsamości. Sprowadzamy w ten sposób jedno mnożenie wielomianów stopnia 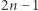 do trzech mnożeń oraz dwóch odejmowań wielomianów stopnia
do trzech mnożeń oraz dwóch odejmowań wielomianów stopnia  Proces ten można kontynuować rekurencyjnie. Liczbę operacji arytmetycznych, wykonywanych przez uzyskany w ten sposób algorytm, opisuje równanie
Proces ten można kontynuować rekurencyjnie. Liczbę operacji arytmetycznych, wykonywanych przez uzyskany w ten sposób algorytm, opisuje równanie 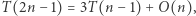 którego rozwiązaniem jest
którego rozwiązaniem jest 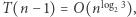 gdzie
gdzie 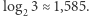 Jeśli początkowe stopnie nie są postaci
Jeśli początkowe stopnie nie są postaci 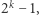 należy je sztucznie zwiększyć, nie zmienia to rzędu liczby operacji.
należy je sztucznie zwiększyć, nie zmienia to rzędu liczby operacji.

Istnieją też inne efektywne algorytmy mnożenia wielomianów. Najszybszy z nich korzysta z szybkiej transformaty Fouriera i wymaga 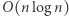 operacji arytmetycznych. Warto zwrócić uwagę, że algorytmów tych można używać także do mnożenia liczb, wstawiając za współczynniki wielomianów cyfry liczb, które chcemy pomnożyć. Poprawność tej procedury łatwo uzasadnić - wystarczy podstawić za
operacji arytmetycznych. Warto zwrócić uwagę, że algorytmów tych można używać także do mnożenia liczb, wstawiając za współczynniki wielomianów cyfry liczb, które chcemy pomnożyć. Poprawność tej procedury łatwo uzasadnić - wystarczy podstawić za 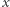 bazę systemu, w którym liczymy, np.
bazę systemu, w którym liczymy, np. 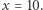 Zarówno algorytm Karatsuby, jak i inne szybkie algorytmy mnożenia liczb/wielomianów są używane w praktyce. Wiele bibliotek implementuje kilka różnych algorytmów i wybiera właściwy w zależności od rozmiaru mnożonych liczb.
Zarówno algorytm Karatsuby, jak i inne szybkie algorytmy mnożenia liczb/wielomianów są używane w praktyce. Wiele bibliotek implementuje kilka różnych algorytmów i wybiera właściwy w zależności od rozmiaru mnożonych liczb.
Przejdźmy teraz do głównego tematu tego artykułu, czyli mnożenia macierzy. Niech 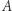 i
i 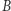 będą macierzami
będą macierzami 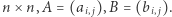 Iloczynem
Iloczynem 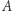 i
i 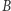 jest macierz
jest macierz 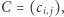 gdzie
gdzie 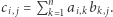 Jak łatwo sprawdzić, mnożenie macierzy za pomocą tej definicji wymaga rzędu
Jak łatwo sprawdzić, mnożenie macierzy za pomocą tej definicji wymaga rzędu 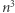 operacji. W 1969 roku Strassen zadziwił świat naukowy odkryciem algorytmu, który mnoży macierze za pomocą
operacji. W 1969 roku Strassen zadziwił świat naukowy odkryciem algorytmu, który mnoży macierze za pomocą 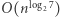 operacji, gdzie
operacji, gdzie 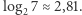 Algorytm ten opiera się na pomyśle podobnym do algorytmu Karatsuby. Strassen znalazł mianowicie metodę mnożenia dwóch macierzy
Algorytm ten opiera się na pomyśle podobnym do algorytmu Karatsuby. Strassen znalazł mianowicie metodę mnożenia dwóch macierzy 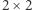 za pomocą
za pomocą 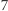 mnożeń zamiast
mnożeń zamiast 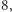 które wykonuje algorytm naiwny. Aby móc zastosować algorytm Strassena rekurencyjnie, wystarczy zauważyć, że jeśli każdą z macierzy
które wykonuje algorytm naiwny. Aby móc zastosować algorytm Strassena rekurencyjnie, wystarczy zauważyć, że jeśli każdą z macierzy 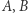 oraz
oraz 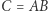 podzielimy na cztery identycznych rozmiarów kwadratowe bloki, to zachodzi:
podzielimy na cztery identycznych rozmiarów kwadratowe bloki, to zachodzi:

Oznacza to, że można takie macierze blokowe mnożyć tak, jakby bloki były liczbami. W połączeniu ze sztuczką Strassena pozwala to zredukować mnożenie macierzy 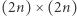 do
do 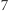 mnożeń macierzy
mnożeń macierzy 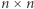 i pewnej, zupełnie nieistotnej, liczby dodawań takich macierzy. Złożoność uzyskanego w efekcie algorytmu rekurencyjnego opisuje równanie
i pewnej, zupełnie nieistotnej, liczby dodawań takich macierzy. Złożoność uzyskanego w efekcie algorytmu rekurencyjnego opisuje równanie 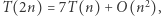 którego rozwiązaniem jest wspomniana wcześniej złożoność
którego rozwiązaniem jest wspomniana wcześniej złożoność 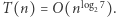
Po odkryciu Strassena sądzono, że znalezienie algorytmu o złożoności 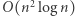 lub podobnej jest tylko kwestią czasu. Stało się jednak inaczej. Przez kolejnych dwadzieścia lat rozwinięto niezwykle wyrafinowaną metodologię konstrukcji algorytmów mnożenia macierzy, wyrażoną w języku algebry tensorowej. W ramach tej teorii zaproponowano wiele algorytmów mnożenia macierzy, najszybszym z nich jest opublikowany w roku 1980 algorytm Coppersmitha i Winograda o złożoności
lub podobnej jest tylko kwestią czasu. Stało się jednak inaczej. Przez kolejnych dwadzieścia lat rozwinięto niezwykle wyrafinowaną metodologię konstrukcji algorytmów mnożenia macierzy, wyrażoną w języku algebry tensorowej. W ramach tej teorii zaproponowano wiele algorytmów mnożenia macierzy, najszybszym z nich jest opublikowany w roku 1980 algorytm Coppersmitha i Winograda o złożoności 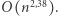 Od tamtego czasu powstały nowe, dużo bardziej eleganckie teorie, m.in. interpretacja znanych algorytmów w języku działań grup. Parametry algorytmu Coppersmitha i Winograda zostały też zoptymalizowane, w efekcie uzyskano złożoność
Od tamtego czasu powstały nowe, dużo bardziej eleganckie teorie, m.in. interpretacja znanych algorytmów w języku działań grup. Parametry algorytmu Coppersmitha i Winograda zostały też zoptymalizowane, w efekcie uzyskano złożoność 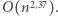 Pytanie o algorytm o złożoności niemal kwadratowej pozostaje nadal jednym z najbardziej fundamentalnych otwartych problemów algorytmiki.
Pytanie o algorytm o złożoności niemal kwadratowej pozostaje nadal jednym z najbardziej fundamentalnych otwartych problemów algorytmiki.
Nie jest to jednak jedyny otwarty problem związany z mnożeniem macierzy. Mnożenie macierzy jest niezwykle często wykorzystywane w praktyce, choćby w implementacji warstw gęstych w tak ostatnio popularnych sieciach neuronowych. Pomimo to żadna z popularnych zoptymalizowanych implementacji nie korzysta z omawianych tu algorytmów. Powody ku temu są dwa. W przypadku najszybszych asymptotycznie algorytmów stała ukryta w notacji dużego 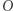 ma monstrualne rozmiary, przez co są one bezużyteczne w praktyce. Z kolei w przypadku wolniejszych asymptotycznie algorytmów, np. algorytmu Strassena, rekurencyjna struktura utrudnia efektywne zarządzanie pamięcią podręczną procesora (cache), które jest kluczowym elementem efektywnych implementacji. Czy istnieją naprawdę szybkie algorytmy mnożenia macierzy?
ma monstrualne rozmiary, przez co są one bezużyteczne w praktyce. Z kolei w przypadku wolniejszych asymptotycznie algorytmów, np. algorytmu Strassena, rekurencyjna struktura utrudnia efektywne zarządzanie pamięcią podręczną procesora (cache), które jest kluczowym elementem efektywnych implementacji. Czy istnieją naprawdę szybkie algorytmy mnożenia macierzy?