Informatyczny kącik olimpijski
Piramidy
Tym razem omówimy zadanie z XII OIG.
Zadanie. Dana jest prostokątna plansza 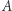 o wymiarach
o wymiarach 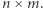 Wiersze zostały ponumerowane od 1 do
Wiersze zostały ponumerowane od 1 do 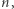 zaś kolumny od 1 do
zaś kolumny od 1 do 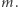 Pole
Pole 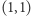 znajduje się w lewym górnym rogu planszy. Niektóre pola mają przypisaną wartość
znajduje się w lewym górnym rogu planszy. Niektóre pola mają przypisaną wartość 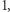 pozostałe wartość 0 (
pozostałe wartość 0 ( ![A[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/7x-439a5e6a621d17059a424f0ccc2881fd26366f00-im-33,33,33-FF,FF,FF.gif) oznacza wartość pola
oznacza wartość pola 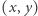 ). Zerowym kwadratem nazywamy kwadrat, który pokrywa tylko zera. Dla każdej liczby całkowitej
). Zerowym kwadratem nazywamy kwadrat, który pokrywa tylko zera. Dla każdej liczby całkowitej  z przedziału
z przedziału ![[1;min(n, m)]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/10x-439a5e6a621d17059a424f0ccc2881fd26366f00-im-33,33,33-FF,FF,FF.gif) należy policzyć, ile jest zerowych kwadratów o boku
należy policzyć, ile jest zerowych kwadratów o boku 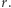
Wstęp
Naszym zadaniem jest obliczenie wartości 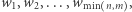 gdzie
gdzie 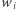 oznacza liczbę zerowych kwadratów o boku
oznacza liczbę zerowych kwadratów o boku 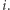 Załóżmy przez chwilę, że dla każdego pola
Załóżmy przez chwilę, że dla każdego pola 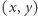 mamy obliczoną wartość
mamy obliczoną wartość ![[x][y] |D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/5x-66ab29750ee0f05b9b12308070e52d3d0745e389-im-33,33,33-FF,FF,FF.gif) - rozmiar największego zerowego kwadratu, którego prawym dolnym rogiem jest pole
- rozmiar największego zerowego kwadratu, którego prawym dolnym rogiem jest pole 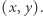 Zauważmy, że pole
Zauważmy, że pole 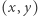 jest również prawym dolnym rogiem zerowych kwadratów o boku:
jest również prawym dolnym rogiem zerowych kwadratów o boku: ![[x][y]. 1,2,...,D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/8x-66ab29750ee0f05b9b12308070e52d3d0745e389-im-33,33,33-FF,FF,FF.gif) Rozważmy teraz ciąg
Rozważmy teraz ciąg 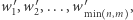 gdzie
gdzie 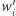 oznacza liczbę wystąpień wartości
oznacza liczbę wystąpień wartości 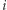 w tablicy
w tablicy 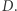
Wówczas 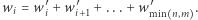
Sumy prefiksowe
Niech ![S[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/1x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) oznacza sumę wartości w prostokącie, którego lewe górne pole ma współrzędne
oznacza sumę wartości w prostokącie, którego lewe górne pole ma współrzędne 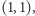 zaś prawe dolne
zaś prawe dolne 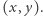 Formalnie:
Formalnie: ![|S[x][y] = Px Py A[i][j]. i 1 j 1](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/4x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) Obliczenie tablicy sum prefiksowych można zrealizować w czasie liniowym względem rozmiaru prostokąta, korzystając z poniższych zależności:
Obliczenie tablicy sum prefiksowych można zrealizować w czasie liniowym względem rozmiaru prostokąta, korzystając z poniższych zależności:
![S[1][1] = A[1][1]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/6x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) ;
;![S[x][1] = S[x − 1][1] +A[x][1]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/8x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) dla
dla 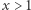 ;
;![S[1][y] = S[1][y −1] +A[1][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/11x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) dla
dla 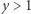 ;
;![S[x][y] = A[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/14x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif)
![S[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/15x-e95ab2e8b63d63e073934ea7ff0dd7bbbec18b93-im-33,33,33-FF,FF,FF.gif) jest sumą: wartości pola
jest sumą: wartości pola 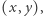 prostokąta bez ostatniego wiersza, prostokąta bez ostatniej kolumny, pomniejszoną o sumę prostokąta bez ostatniego wiersza i ostatniej kolumny, który został dodany dwa razy.
prostokąta bez ostatniego wiersza, prostokąta bez ostatniej kolumny, pomniejszoną o sumę prostokąta bez ostatniego wiersza i ostatniej kolumny, który został dodany dwa razy.
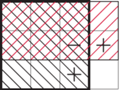
Zastanówmy się teraz, jak za pomocą tablicy sum prefiksowych obliczyć sumę wartości w prostokącie w czasie stałym. Niech 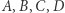 będą prostokątami, których lewe górne pole ma współrzędne
będą prostokątami, których lewe górne pole ma współrzędne 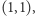 zaś prawe dolne pole zostało wskazane na poniższym rysunku.
zaś prawe dolne pole zostało wskazane na poniższym rysunku.
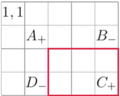
Załóżmy, że chcemy obliczyć sumę wartości w kolorowym prostokącie. Jest to 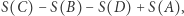 gdzie
gdzie 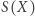 oznacza sumę wartości w prostokącie
oznacza sumę wartości w prostokącie 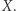
Rozwiązanie 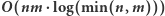
W tym podejściu wyznaczymy wartości tablicy 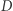 przy wykorzystaniu metody wyszukiwania binarnego po wyniku. Załóżmy, że chcemy obliczyć wartość
przy wykorzystaniu metody wyszukiwania binarnego po wyniku. Załóżmy, że chcemy obliczyć wartość ![[x][y] |D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/3x-6d0545a67f88dab35840192a8d60aa19baea3113-im-33,33,33-FF,FF,FF.gif) dla ustalonych
dla ustalonych 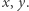 Jeśli
Jeśli ![|A[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/5x-6d0545a67f88dab35840192a8d60aa19baea3113-im-33,33,33-FF,FF,FF.gif) wtedy
wtedy ![[x][y]=0.D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/6x-6d0545a67f88dab35840192a8d60aa19baea3113-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku
W przeciwnym przypadku ![[x][y] D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/7x-6d0545a67f88dab35840192a8d60aa19baea3113-im-33,33,33-FF,FF,FF.gif) jest liczbą całkowitą z przedziału
jest liczbą całkowitą z przedziału ![|[1;min(x, y)].](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/8x-6d0545a67f88dab35840192a8d60aa19baea3113-im-33,33,33-FF,FF,FF.gif) Tę wartość możemy wyszukać binarnie po wyniku, korzystając z faktu:
Tę wartość możemy wyszukać binarnie po wyniku, korzystając z faktu:
Fakt. Jeśli 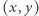 jest prawym dolnym rogiem zerowego kwadratu o boku
jest prawym dolnym rogiem zerowego kwadratu o boku 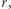 to jest również prawym dolnym rogiem każdego mniejszego zerowego kwadratu.
to jest również prawym dolnym rogiem każdego mniejszego zerowego kwadratu.
Sprawdzenie, czy 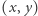 jest prawym dolnym rogiem zerowego kwadratu o boku
jest prawym dolnym rogiem zerowego kwadratu o boku 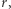 można wykonać za pomocą sum prefiksowych w czasie
można wykonać za pomocą sum prefiksowych w czasie 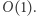 Algorytm wyszukiwania binarnego wykona
Algorytm wyszukiwania binarnego wykona 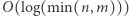 takich faz. Wszystkich pól jest
takich faz. Wszystkich pól jest 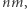 zatem wyznaczenie tablicy
zatem wyznaczenie tablicy 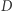 działa w czasie
działa w czasie
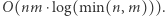
Rozwiązanie dynamiczne 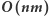
W tym podejściu wyznaczymy wartości tablicy 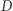 przy wykorzystaniu metody programowania dynamicznego. Załóżmy, że chcemy obliczyć wartość
przy wykorzystaniu metody programowania dynamicznego. Załóżmy, że chcemy obliczyć wartość ![[x][y] |D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/3x-50cb24976cae49e2be805b1e333b2483ff71c4ed-im-33,33,33-FF,FF,FF.gif) dla ustalonych
dla ustalonych 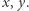 Jeśli
Jeśli ![|A[x][y]](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/5x-50cb24976cae49e2be805b1e333b2483ff71c4ed-im-33,33,33-FF,FF,FF.gif) wtedy
wtedy ![[x][y]=0.D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/6x-50cb24976cae49e2be805b1e333b2483ff71c4ed-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku rozpatrujemy następujące możliwości.
W przeciwnym przypadku rozpatrujemy następujące możliwości.
- Jeśli
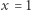 lub
lub 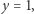 wtedy
wtedy ![[x][y]=1. D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/4x-d2647d627ae1147f0c8df96868f0873a42c0b48d-im-33,33,33-FF,FF,FF.gif) Dla wszystkich pól w pierwszym wierszu oraz w pierwszej kolumnie największy kwadrat ma rozmiar
Dla wszystkich pól w pierwszym wierszu oraz w pierwszej kolumnie największy kwadrat ma rozmiar 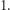
- Jeśli
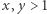 oraz
oraz ![[x−1][y]/=D[x][y−1], |D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/8x-d2647d627ae1147f0c8df96868f0873a42c0b48d-im-33,33,33-FF,FF,FF.gif) wtedy
wtedy ![[x][y]=1+min(D[x−1][y],D[x][y−1]). D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/9x-d2647d627ae1147f0c8df96868f0873a42c0b48d-im-33,33,33-FF,FF,FF.gif)
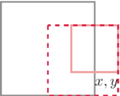
- Jeśli
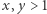 oraz
oraz ![[x−1][y]=D[x][y−1], |D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/3x-3a546395ae79ff0bacae3ab960a2bd23d9f987a6-im-33,33,33-FF,FF,FF.gif) wtedy
wtedy ![[x][y]=k+l, D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/4x-3a546395ae79ff0bacae3ab960a2bd23d9f987a6-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie ![[x−1][y], k = D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/5x-3a546395ae79ff0bacae3ab960a2bd23d9f987a6-im-33,33,33-FF,FF,FF.gif) zaś
zaś 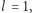 jeśli
jeśli 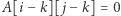 i
i 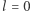 w przeciwnym przypadku.
w przeciwnym przypadku.
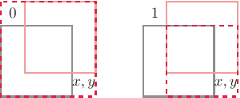
Obliczenie wartości ![[x][y] D](/math/temat/informatyka/algorytmy/2018/09/30/Piramidy/1x-6b2b4c092682335767a234383e31f1ad0db8f871-im-33,33,33-FF,FF,FF.gif) dla ustalonego
dla ustalonego 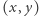 odbywa się w czasie
odbywa się w czasie 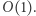 Plansza ma
Plansza ma 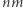 pól, zatem wyznaczenie tablicy
pól, zatem wyznaczenie tablicy 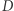 działa w czasie
działa w czasie