Informatyczny kącik olimpijski
Piramida liczbowa i Żabka
Tym razem omówimy dwa zadania z zawodów drużynowych X Olimpiady Informatycznej Gimnazjalistów.

Zadanie (Piramida liczbowa). Julia postanowiła zbudować piramidę liczbową. Budowę rozpoczęła od wypisania swojego ulubionego 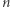 -elementowego ciągu
-elementowego ciągu 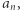 który stanowił podstawę konstrukcji. Następnie, dla każdej pary sąsiednich liczb napisała nad nią większą z nich. Zauważmy, że każde kolejne piętro jest o jedną liczbę krótsze od poprzedniego. Naszym zadaniem jest obliczyć sumę elementów tej piramidy. Po prawej znajduje się przykład piramidy, której podstawę stanowi ciąg
który stanowił podstawę konstrukcji. Następnie, dla każdej pary sąsiednich liczb napisała nad nią większą z nich. Zauważmy, że każde kolejne piętro jest o jedną liczbę krótsze od poprzedniego. Naszym zadaniem jest obliczyć sumę elementów tej piramidy. Po prawej znajduje się przykład piramidy, której podstawę stanowi ciąg 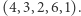
Rozwiązanie 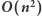
Pierwszym pomysłem, który nasuwa się na myśl, jest wygenerowanie piramidy, która składa się z 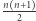 liczb, a następnie zsumowanie tych wartości. Takie rozwiązanie działa w czasie
liczb, a następnie zsumowanie tych wartości. Takie rozwiązanie działa w czasie 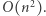
Rozwiązanie 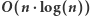
Zauważmy, że zbiór wartości, które występują w całej piramidzie, jest równy zbiorowi wartości, które występują w podstawie tej piramidy. Wynika to bezpośrednio z konstrukcji piramidy. W związku z tym dla każdego elementu w podstawie piramidy obliczymy, ile razy występuje on w piramidzie. Wybierzmy maksymalny element w podstawie (jeśli jest więcej niż jeden taki element, wtedy wybieramy dowolny z nich), oznaczmy go przez 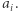
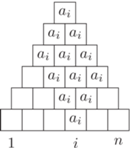
Na rysunku zaznaczono elementy piramidy o wartości 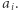 Pozostałe elementy tworzą dwie mniejsze piramidy. Jedna o podstawie
Pozostałe elementy tworzą dwie mniejsze piramidy. Jedna o podstawie 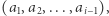 druga zaś o podstawie
druga zaś o podstawie 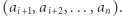 Wartość
Wartość 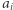 występuje:
występuje:

razy w piramidzie (jest to rozmiar całej piramidy pomniejszony o rozmiar lewej oraz prawej piramidy). Suma wszystkich elementów w piramidzie to 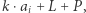 gdzie
gdzie 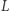 jest sumą elementów lewej piramidy
jest sumą elementów lewej piramidy 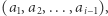 zaś
zaś 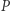 jest sumą elementów prawej piramidy
jest sumą elementów prawej piramidy 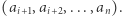 Aby obliczyć
Aby obliczyć 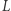 i
i 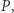 wystarczy opisaną procedurę wywołać rekurencyjnie.
wystarczy opisaną procedurę wywołać rekurencyjnie.
Pozostało nam jeszcze zastanowić się, jak znajdować numer maksymalnego elementu w przedziale. Oczywiście, możemy naiwnie przejrzeć cały przedział i wybrać maksimum. Niestety, wówczas otrzymamy rozwiązanie, które działa w czasie 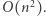 W celu przyspieszenia znajdowania maksimum w przedziale możemy wykorzystać drzewo przedziałowe, które w każdym węźle przechowuje dwie wartości: wartość największego elementu oraz numer tego elementu. Wówczas otrzymujemy rozwiązanie, które działa w czasie
W celu przyspieszenia znajdowania maksimum w przedziale możemy wykorzystać drzewo przedziałowe, które w każdym węźle przechowuje dwie wartości: wartość największego elementu oraz numer tego elementu. Wówczas otrzymujemy rozwiązanie, które działa w czasie 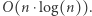
Zadanie (Żabka). Żabka o imieniu Bajtuś znajduje się na kamieniu numer 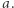 Natomiast jej upragniona mucha znajduje się na kamieniu numer
Natomiast jej upragniona mucha znajduje się na kamieniu numer 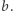 Żabka w jednym skoku z kamienia numer
Żabka w jednym skoku z kamienia numer  może przemieścić się na kamień o numerze
może przemieścić się na kamień o numerze 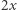 lub
lub 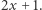 Czy istnieje taka sekwencja ruchów, która pozwoli Bajtusiowi dotrzeć do muchy?
Czy istnieje taka sekwencja ruchów, która pozwoli Bajtusiowi dotrzeć do muchy?
Na początku rozważmy trywialny przypadek. Jeśli 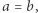 wtedy, oczywiście, Bajtuś dotarł już do muchy. Załóżmy zatem, że
wtedy, oczywiście, Bajtuś dotarł już do muchy. Załóżmy zatem, że 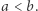 W pierwszym skoku Bajtuś może skoczyć na kamienie numer
W pierwszym skoku Bajtuś może skoczyć na kamienie numer 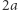 oraz
oraz 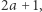 innymi słowy na kamienie o numerach całkowitych z przedziału
innymi słowy na kamienie o numerach całkowitych z przedziału ![[2a;2a + 1].](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/5x-9ed0989ad7e1742df3673c71eaea77f1e6656284-im-33,33,33-FF,FF,FF.gif) W drugim skoku Bajtuś może skoczyć na kamienie numer
W drugim skoku Bajtuś może skoczyć na kamienie numer 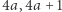 z kamienia numer
z kamienia numer 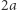 oraz na kamienie numer
oraz na kamienie numer 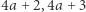 z kamienia numer
z kamienia numer 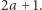 Zatem po wykonaniu dwóch skoków Bajtuś może znaleźć się na kamieniach o numerach całkowitych z przedziału
Zatem po wykonaniu dwóch skoków Bajtuś może znaleźć się na kamieniach o numerach całkowitych z przedziału ![[4a;4a + 3].](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/10x-9ed0989ad7e1742df3673c71eaea77f1e6656284-im-33,33,33-FF,FF,FF.gif)
Obserwacja: Jeśli w 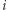 skokach Bajtuś może osiągnąć kamienie numer
skokach Bajtuś może osiągnąć kamienie numer ![[c;d],](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/2x-3a91f4b9fb91a94d6a1e75dec024cc28abd5cdbc-im-33,33,33-FF,FF,FF.gif) to po
to po 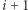 skokach może osiągnąć kamienie numer
skokach może osiągnąć kamienie numer ![|[2c;2d + 1].](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/4x-3a91f4b9fb91a94d6a1e75dec024cc28abd5cdbc-im-33,33,33-FF,FF,FF.gif)
Dowód: Rozważmy dwa przypadki:
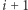 -wszy skok jest typu
-wszy skok jest typu 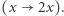 Wówczas Bajtuś może osiągnąć kamienie numer
Wówczas Bajtuś może osiągnąć kamienie numer 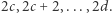
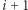 -wszy skok jest typu
-wszy skok jest typu 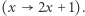 Wówczas Bajtuś może osiągnąć kamienie numer
Wówczas Bajtuś może osiągnąć kamienie numer 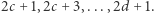
Zatem każdy z kamieni numer ![[2c;2d + 1]](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/9x-4c3a011b4066357b6b00efd08210fe979587425d-im-33,33,33-FF,FF,FF.gif) jest osiągalny przez Bajtusia po
jest osiągalny przez Bajtusia po 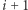 skokach.
skokach.
Na podstawie powyższej obserwacji generujemy przedziały numerów kamieni, które są osiągalne przez Bajtusia w kolejnych skokach:
![[8a; 8a+ 7], [16a;16a +15], [32a;32a + 31],....](/math/temat/informatyka/algorytmy/2018/07/24/Piramida_liczbowa_i_Zabka/1x-f3b4188faae9404bbe4b2045f566ce407ca5e911-dm-33,33,33-FF,FF,FF.gif)
Następnie sprawdzamy, czy istnieje przedział, którego początek jest nie większy niż 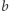 oraz
oraz 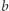 do niego należy.
do niego należy.
Zauważmy, że numery początków kolejnych przedziałów rosną wykładniczo. Zatem rozwiązanie działa w czasie