Informatyczny kącik olimpijski
Bajtockie kółeczko
Tym razem omówimy zadanie Bajtockie kółeczko z pierwszego etapu zawodów drużynowych X Olimpiady Informatycznej Gimnazjalistów.
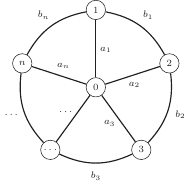
Problem (Bajtockie kółeczko). W Bajtocji znajduje się 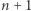 miast (ponumerowanych kolejnymi liczbami naturalnymi od 0 do
miast (ponumerowanych kolejnymi liczbami naturalnymi od 0 do 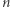 ) oraz
) oraz 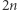 dróg pomiędzy nimi. Miasta o numerach z przedziału
dróg pomiędzy nimi. Miasta o numerach z przedziału ![|[1;n]](/math/temat/informatyka/algorytmy/2018/06/30/Bajtockie_koleczko/4x-922730eed2dbed93b71a8234a1ae83004fb096d2-im-33,33,33-FF,FF,FF.gif) znajdują się na okręgu, zaś miasto o numerze 0 (stolica) jest środkiem tego okręgu. Pomiędzy każdym miastem na okręgu oraz stolicą istnieje dwukierunkowe połączenie (
znajdują się na okręgu, zaś miasto o numerze 0 (stolica) jest środkiem tego okręgu. Pomiędzy każdym miastem na okręgu oraz stolicą istnieje dwukierunkowe połączenie ( 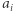 oznacza czas przejazdu pomiędzy stolicą a
oznacza czas przejazdu pomiędzy stolicą a 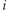 -tym miastem). Dodatkowo, pomiędzy każdymi dwoma sąsiednimi miastami na okręgu istnieje dwukierunkowe połączenie (
-tym miastem). Dodatkowo, pomiędzy każdymi dwoma sąsiednimi miastami na okręgu istnieje dwukierunkowe połączenie ( 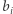 oznacza czas przejazdu pomiędzy
oznacza czas przejazdu pomiędzy 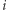 -tym miastem a miastem sąsiadującym z prawej strony). Naszym zadaniem jest zaplanowanie podróży po Bajtocji. W tym celu musimy wybrać miasto, z którego wyruszymy oraz miasta, które odwiedzimy. Podróż musi zaczynać się i kończyć w tym samym mieście. Każda droga oraz każde miasto (poza miastem, w którym zaczynamy i kończymy podróż) może zostać odwiedzone co najwyżej raz. Ile czasu potrwa najdłuższa taka podróż?
-tym miastem a miastem sąsiadującym z prawej strony). Naszym zadaniem jest zaplanowanie podróży po Bajtocji. W tym celu musimy wybrać miasto, z którego wyruszymy oraz miasta, które odwiedzimy. Podróż musi zaczynać się i kończyć w tym samym mieście. Każda droga oraz każde miasto (poza miastem, w którym zaczynamy i kończymy podróż) może zostać odwiedzone co najwyżej raz. Ile czasu potrwa najdłuższa taka podróż?
Naszym zadaniem, w terminologii grafowej, jest znalezienie cyklu o największej sumie wag krawędzi. Rozważmy dwa przypadki:
- do cyklu nie należy wierzchołek 0 - wówczas mamy tylko jedną możliwość wyboru cyklu, którego suma wag krawędzi wynosi:
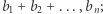
- do cyklu należy wierzchołek 0 - ten przypadek zostanie dokładnie opisany w dalszej części rozwiązania.
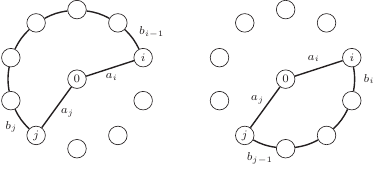
Po lewej 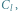 po prawej
po prawej 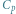
Rozwiązanie 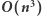
Rozważamy przypadek, kiedy stolica należy do cyklu. W tym przypadku dokładnie dwie krawędzie incydentne ze stolicą należą do cyklu. Zauważmy, że dla ustalonych krawędzi incydentnych ze stolicą łatwo znaleźć najdłuższy cykl. Załóżmy, że do cyklu należą krawędzie: 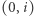 oraz
oraz 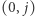 dla
dla ![|i, j ∈[1;n]](/math/temat/informatyka/algorytmy/2018/06/30/Bajtockie_koleczko/4x-eeebb9f1a20e6e78c101c182fe30eabbe0727a2b-im-33,33,33-FF,FF,FF.gif) i
i 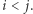 Wówczas istnieją dokładnie dwa cykle zawierające obie te krawędzi:
Wówczas istnieją dokładnie dwa cykle zawierające obie te krawędzi:
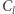 - zakładamy, że od
- zakładamy, że od 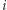 -tego wierzchołka poruszamy się w lewo,
-tego wierzchołka poruszamy się w lewo,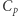 - zakładamy, że od
- zakładamy, że od 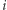 -tego wierzchołka poruszamy się w prawo.
-tego wierzchołka poruszamy się w prawo.
Suma wag krawędzi cyklu 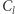 wynosi:
wynosi:

zaś suma wag krawędzi cyklu 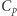 wynosi:
wynosi:

Zatem dla ustalonych krawędzi incydentnych ze stolicą (krawędzi do wierzchołków 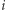 oraz
oraz 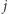 ) wynikiem jest
) wynikiem jest 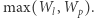
Aby znaleźć cykl o największej sumie wag krawędzi, wystarczy rozpatrzyć każdą parę krawędzi incydentnych ze stolicą. Dla każdej takiej pary należy obliczyć wynik i spośród otrzymanych wyników wybrać maksimum. W ten sposób otrzymujemy rozwiązanie, które działa w czasie 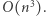
Rozwiązanie 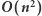
Zauważmy, że możemy w czasie stałym obliczać sumę wag krawędzi na spójnym fragmencie obwodu przy wykorzystaniu sum prefiksowych. Wówczas otrzymujemy rozwiązanie, które działa w czasie 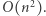
Rozwiązanie 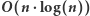
Ustawmy wierzchołki, które znajdują się na obwodzie, w ciąg (jeden za drugim) oraz zduplikujmy otrzymany ciąg.
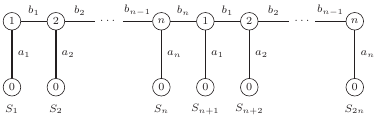
Niech 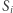 oznacza odległość od wierzchołka numer
oznacza odległość od wierzchołka numer 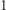 do kolejnych kopii stolicy, dokładnie:
do kolejnych kopii stolicy, dokładnie:

Dla każdego całkowitego ![i ∈[1;n]](/math/temat/informatyka/algorytmy/2018/06/30/Bajtockie_koleczko/4x-cceccd373eef65bf2d1c5fce977d015867962dbf-im-33,33,33-FF,FF,FF.gif) znajdujemy najdłuższy cykl, który zawiera krawędź
znajdujemy najdłuższy cykl, który zawiera krawędź 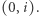 Zauważmy, że długość tego cyklu wynosi:
Zauważmy, że długość tego cyklu wynosi: 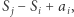 dla takiego największego
dla takiego największego 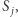 że
że ![| j ∈[i + 1;i + n− 1].](/math/temat/informatyka/algorytmy/2018/06/30/Bajtockie_koleczko/8x-cceccd373eef65bf2d1c5fce977d015867962dbf-im-33,33,33-FF,FF,FF.gif) Znalezienie największej takiej wartości w ciągu
Znalezienie największej takiej wartości w ciągu 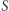 można zrealizować drzewem przedziałowym (dlaczego?). Spośród wyników obliczonych dla każdego
można zrealizować drzewem przedziałowym (dlaczego?). Spośród wyników obliczonych dla każdego ![|i∈[1;n]](/math/temat/informatyka/algorytmy/2018/06/30/Bajtockie_koleczko/10x-cceccd373eef65bf2d1c5fce977d015867962dbf-im-33,33,33-FF,FF,FF.gif) wybieramy największy. W ten sposób otrzymujemy rozwiązanie, które działa w czasie
wybieramy największy. W ten sposób otrzymujemy rozwiązanie, które działa w czasie 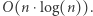
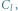 po prawej
po prawej