Informatyczny kącik olimpijski
Liczby
W tym miesiącu omówimy zadanie Liczby, które pojawiło się podczas rundy 72. na portalu codeforces.com.
W zadaniu należy, mając dane liczby naturalne 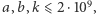 wyznaczyć liczbę liczb naturalnych w przedziale
wyznaczyć liczbę liczb naturalnych w przedziale ![[a,b],](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/2x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) których najmniejszym dzielnikiem, większym od
których najmniejszym dzielnikiem, większym od 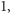 jest
jest 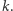 Zauważmy najpierw, że wystarczy umieć obliczać wyniki dla przedziałów postaci
Zauważmy najpierw, że wystarczy umieć obliczać wyniki dla przedziałów postaci ![[1,n],](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/5x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) ponieważ wynik dla przedziału
ponieważ wynik dla przedziału ![[a,b]](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/6x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) jest różnicą wyników dla przedziałów
jest różnicą wyników dla przedziałów ![|[1,b]](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/7x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) i
i ![[1,a −1].](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/8x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) Ponadto, jeśli
Ponadto, jeśli 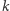 nie jest liczbą pierwszą, to wynik jest równy 0, ponieważ jeśli liczba jest podzielna przez
nie jest liczbą pierwszą, to wynik jest równy 0, ponieważ jeśli liczba jest podzielna przez 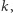 to jest też podzielna przez każdy dzielnik
to jest też podzielna przez każdy dzielnik 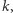 a skoro
a skoro 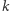 nie jest pierwsza, to ma dzielnik większy od
nie jest pierwsza, to ma dzielnik większy od 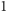 i mniejszy od
i mniejszy od 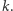 Załóżmy teraz, że
Załóżmy teraz, że 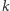 jest pierwsza. Zadanie można rozwiązać w czasie
jest pierwsza. Zadanie można rozwiązać w czasie 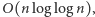 wyznaczając dla każdej liczby z przedziału
wyznaczając dla każdej liczby z przedziału ![|[1,n]](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/17x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) jej najmniejszy dzielnik, większy od 1, za pomocą sita Eratostenesa. Rozwiązanie to dla
jej najmniejszy dzielnik, większy od 1, za pomocą sita Eratostenesa. Rozwiązanie to dla 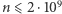 jest dalece niewystarczające. Zauważmy, że można je łatwo usprawnić. Każda liczba, której najmniejszy dzielnik jest równy
jest dalece niewystarczające. Zauważmy, że można je łatwo usprawnić. Każda liczba, której najmniejszy dzielnik jest równy 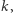 jest postaci
jest postaci 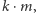 gdzie
gdzie 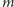 nie ma dzielników większych od
nie ma dzielników większych od 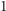 i mniejszych od
i mniejszych od 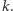 Wystarczy zatem zliczyć takie
Wystarczy zatem zliczyć takie 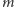 -y z przedziału
-y z przedziału ![[1, | ⌊n⌋], k](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/25x-70fdc1ace2e0004236ebd6525396e1a926888ec5-im-33,33,33-FF,FF,FF.gif) które nie mają dzielników pierwszych mniejszych od
które nie mają dzielników pierwszych mniejszych od 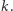 Można to zrobić, iterując kolejne liczby pierwsze mniejsze od
Można to zrobić, iterując kolejne liczby pierwsze mniejsze od 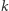 i zaznaczając w tablicy liczby podzielne przez którąś z nich.
i zaznaczając w tablicy liczby podzielne przez którąś z nich.
Rozwiązanie to wykona dla każdej liczby pierwszej 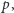 mniejszej od
mniejszej od 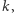
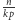 operacji, czyli łącznie
operacji, czyli łącznie

Dla 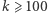 rozwiązanie takie jest wystarczające. Jeśli natomiast
rozwiązanie takie jest wystarczające. Jeśli natomiast 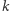 jest mniejsze od
jest mniejsze od 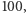 to liczb pierwszych mniejszych od
to liczb pierwszych mniejszych od 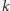 jest nie więcej niż
jest nie więcej niż 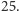 Niech teraz
Niech teraz 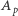 oznacza zbiór liczb podzielnych przez
oznacza zbiór liczb podzielnych przez 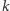 oraz
oraz 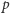 leżących w przedziale
leżących w przedziale ![[1,n].](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/13x-d7d892ccd540d7223422dfe09c1914ea7aedc6e3-im-33,33,33-FF,FF,FF.gif) Naszym zadaniem jest obliczenie
Naszym zadaniem jest obliczenie
![{x ∈[1,n] k x}∖ ⎛ A . ⎝ p>P,p@k](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/14x-d7d892ccd540d7223422dfe09c1914ea7aedc6e3-dm-33,33,33-FF,FF,FF.gif)
Możemy to zrobić, korzystając z zasady włączeń i wyłączeń. W tym celu musimy umieć obliczyć 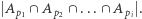 Jest to zbiór liczb podzielnych przez
Jest to zbiór liczb podzielnych przez 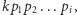 leżących w przedziale
leżących w przedziale ![[1,n],](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/17x-d7d892ccd540d7223422dfe09c1914ea7aedc6e3-im-33,33,33-FF,FF,FF.gif) czyli ma
czyli ma 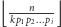 elementów.
elementów.
Całe rozwiązanie działa w czasie

Na to zadanie można też spojrzeć inaczej. Niech 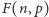 będzie liczbą liczb w przedziale
będzie liczbą liczb w przedziale ![[1,n],](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/3x-843d9054587ca40f4af5014508b22f5dc0d80b84-im-33,33,33-FF,FF,FF.gif) które nie mają dzielników większych od
które nie mają dzielników większych od 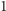 i mniejszych od
i mniejszych od 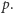 Wykażemy, że
Wykażemy, że

Istotnie, liczb nie większych od 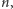 których najmniejszym dzielnikiem jest
których najmniejszym dzielnikiem jest 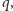 jest
jest 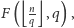 ponieważ każda taka liczba jest postaci
ponieważ każda taka liczba jest postaci 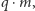 gdzie
gdzie 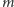 nie ma dzielników większych od
nie ma dzielników większych od 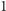 i mniejszych od
i mniejszych od 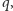 a
a 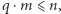 czyli
czyli 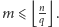 Wszystkich liczb w przedziale
Wszystkich liczb w przedziale ![|[1,n]](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/16x-843d9054587ca40f4af5014508b22f5dc0d80b84-im-33,33,33-FF,FF,FF.gif) jest
jest 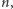 a każda z nich albo ma dzielnik pierwszy mniejszy od
a każda z nich albo ma dzielnik pierwszy mniejszy od 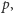 wówczas zostanie odjęta dokładnie raz, dla
wówczas zostanie odjęta dokładnie raz, dla 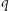 będącego jej najmniejszym dzielnikiem pierwszym, albo nie ma i wtedy nie zostanie odjęta. Liczba liczb w przedziale
będącego jej najmniejszym dzielnikiem pierwszym, albo nie ma i wtedy nie zostanie odjęta. Liczba liczb w przedziale ![| [1,n],](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/20x-843d9054587ca40f4af5014508b22f5dc0d80b84-im-33,33,33-FF,FF,FF.gif) których najmniejszym dzielnikiem jest
których najmniejszym dzielnikiem jest 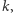 jest równa
jest równa 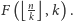 Zadanie można rozwiązać, obliczając wartość funkcji
Zadanie można rozwiązać, obliczając wartość funkcji 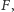 rekurencyjnie korzystając z tego wzoru. Niech
rekurencyjnie korzystając z tego wzoru. Niech 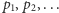 będą kolejnymi liczbami pierwszymi, a
będą kolejnymi liczbami pierwszymi, a 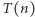 liczbą operacji wykonanych przez algorytm dla liczby pierwszej
liczbą operacji wykonanych przez algorytm dla liczby pierwszej 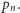 Wówczas
Wówczas 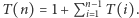 Rozwiązaniem tego równania jest
Rozwiązaniem tego równania jest 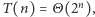 czyli całe rozwiązanie będzie działało w czasie
czyli całe rozwiązanie będzie działało w czasie 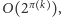 co jest zdecydowanie za wolne.
co jest zdecydowanie za wolne.
Rozwiązanie to można łatwo przyspieszyć. Wystarczy zauważyć, że jeśli 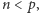 to jedyną liczbą w przedziale
to jedyną liczbą w przedziale ![|[1,n]](/math/temat/informatyka/algorytmy/2017/11/25/Liczby/2x-1e90f23eef7fd3f5bb6d841edaf4a722faf93bb6-im-33,33,33-FF,FF,FF.gif) niemającą dzielników większych od
niemającą dzielników większych od 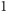 i mniejszych od
i mniejszych od 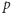 jest
jest 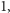 więc
więc 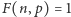 i w każdym wywołaniu rekurencyjnym obliczającym wynik dla
i w każdym wywołaniu rekurencyjnym obliczającym wynik dla 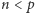 zwracać
zwracać 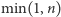 bez dalszych wywołań rekurencyjnych. Wykażemy, że rozwiązanie z tą optymalizacją obliczające
bez dalszych wywołań rekurencyjnych. Wykażemy, że rozwiązanie z tą optymalizacją obliczające 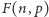 wykona co najwyżej
wykona co najwyżej 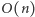 wywołań rekurencyjnych. Rozważmy gałąź w drzewie rekursji, w której algorytm wykonał kolejno dzielenia przez
wywołań rekurencyjnych. Rozważmy gałąź w drzewie rekursji, w której algorytm wykonał kolejno dzielenia przez 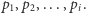 Oznacza to, że w przedostatnim wywołaniu obliczał
Oznacza to, że w przedostatnim wywołaniu obliczał 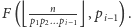 Skoro nie zwrócił wyniku od razu, tylko wykonał następne wykonanie rekurencyjne, to
Skoro nie zwrócił wyniku od razu, tylko wykonał następne wykonanie rekurencyjne, to 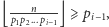 skąd wynika, że
skąd wynika, że 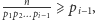 czyli
czyli 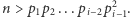 Algorytm w danym wywołaniu przegląda jedynie liczby pierwsze, mniejsze od poprzedniej, zatem
Algorytm w danym wywołaniu przegląda jedynie liczby pierwsze, mniejsze od poprzedniej, zatem 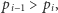 skąd otrzymujemy
skąd otrzymujemy 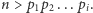 Liczby
Liczby 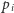 są pierwsze, więc dla różnych wywołań rekurencyjnych iloczyny
są pierwsze, więc dla różnych wywołań rekurencyjnych iloczyny 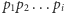 będą parami różne, więc liczba tych wywołań nie przekroczy
będą parami różne, więc liczba tych wywołań nie przekroczy 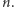
Prezentowane rozwiązanie potrzebuje listy liczb pierwszych mniejszych od 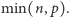 Można ją, oczywiście, wyznaczyć, używając sita Eratostenesa, w czasie
Można ją, oczywiście, wyznaczyć, używając sita Eratostenesa, w czasie 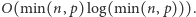 Ostatecznie, całe rozwiązanie obliczające
Ostatecznie, całe rozwiązanie obliczające 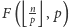 działa w czasie
działa w czasie