Wyobraźmy sobie, że analizujemy kamerę online, która transmituje obraz 24 godziny na dobę i chcemy po miesiącu wydobyć pewne statystyki z tego, co nagrała. Możemy, oczywiście, zapisać całość na dysk i potem obliczyć to, co trzeba. Łatwo sobie jednak wyobrazić, że potrzeba na to wiele pamięci, którą niekoniecznie zamierzamy właśnie na to przeznaczać. Dobrze byłoby na bieżąco obliczać to, co chcemy, i nie zapisywać całego filmu - pamiętać tylko statystyki z przeszłości i uaktualniać je w czasie rzeczywistym. Podobne problemy spotykamy w wielu miejscach, gdy rozważamy duży strumień danych, przykładowo film lub dźwięk, ale również inne, jak ruch pakietów TCP/IP w sieci. Taka jest geneza powstania dziedziny algorytmów strumieniowych, czyli działających na strumieniu danych i obliczających na bieżąco pewne jego własności. Jej matematyczne podstawy są, moim zdaniem, wyjątkowo piękne.

Założymy, że nasz strumień danych to ciąg 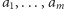dla pewnego dużego 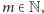oraz że 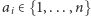dla każdego 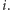Niech 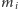będzie liczbą wystąpień liczby 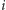w całym strumieniu. Naszym celem będzie obliczenie pewnych własności strumienia w pamięci istotnie mniejszej niż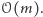

Na początek przyjrzyjmy się następującej zagadce. Rozważmy strumień, w którym pewna wartość występuje więcej niż na połowie miejsc. Czyli istnieje 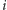takie, że 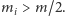Jak wtedy znaleźć 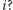Nie jest jasne, jak to zrobić bez trzymania aktualnych wartości 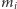dla wszystkich 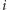podczas przeglądania strumienia. Okazuje się, że działa algorytm naprawdę banalny. W każdej chwili pamiętamy parę liczb. Pierwsza liczba to kandydat na odpowiedź, a druga liczba to coś jakby jego przewaga nad resztą. Inicjalizujemy parę jako 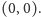Powiedzmy, że po przeczytaniu 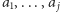pamiętamy parę 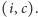Są dwie możliwości. Jeśli 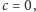to po przeczytaniu 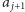ustawiamy parę na 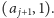Jeśli natomiast 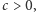to rozważamy dwa przypadki. Jeżeli 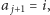to zwiększamy przewagę, czyli ustawiamy 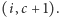Jeśli natomiast 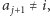to ustawiamy 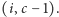Na końcu zwracamy pierwszy element z pary. Zauważmy jednak, że algorytm wcale nie trzyma prawdziwego dotychczasowego rekordzisty wraz z jego przewagą. Po przeczytaniu pierwszych sześciu elementów ciągu 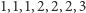będzie trzymał parę 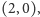a więc po przeczytaniu ostatniego wyrazu parę 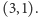Dlaczego więc działa poprawnie? Przypomnijmy, że pewien element 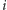występuje na więcej niż połowie miejsc. Niech wartość pary 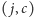będzie równa 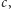o ile 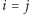oraz 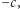o ile 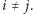Zauważmy, że napotkanie elementu 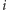zawsze zwiększa o jeden wartość pary, a innego niż 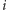- zmniejsza ją lub zwiększa o jeden. Na początku wartość pary to 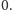Zatem po przeczytaniu całego ciągu wartość pary będzie dodatnia, czyli pierwszy jej element to faktycznie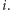

Ważnej informacji o własnościach strumienia dostarczają liczby 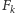zdefiniowane jako 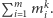Dla 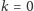to liczba różnych elementów, dla 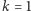to po prostu 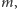a dla 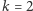jest to ważna miara równomierności występowania wartości w ciągu. Bardzo ładny i elegancki jest przybliżony algorytm liczenia wartości 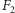w pamięci jedynie 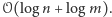My najpierw pokażemy, jak to zrobić w pamięci 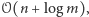co nie jest takie złe, bo to zwykle 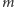jest olbrzymie, a może być niewielkie. Algorytm używa losowości. Dla każdego 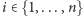losujemy wartość 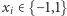tak, że 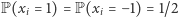oraz losowania są niezależne. Na początek ustalamy licznik na 0 i zaczynamy przeglądać strumień. Gdy czytamy element 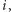to zwiększamy licznik o 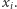Na końcu zwracamy 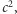twierdząc, że jest to dobre przybliżenie 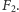Algorytm prosty, ale dlaczego to w ogóle ma działać? Najpierw zauważmy, że każde 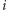zwiększyło wartość o 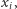czyli w sumie wszystkie 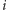zwiększyły go o 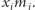A więc na końcu 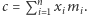Obliczmy wartość oczekiwaną 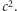Mamy

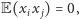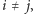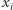Zauważmy, że o ile tylko bo oraz 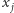są niezależne. A zatem

I ten fakt wydaje się najciekawszy. Wypadałoby jeszcze wykazać, że błąd tego obliczenia (czyli wariancja) jest nie za duży. My tutaj jedynie podamy na wiarę, że 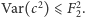Ambitnych Czytelników zachęcamy do przerachowania. Błąd możemy łatwo zmniejszyć, uruchamiając 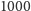takich samych algorytmów równocześnie, a na końcu uśredniając ich wyniki rezultat oznaczmy 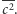Wówczas wartość oczekiwana się nie zmieni, a wariancja zmaleje 1000 razy. Przypomnijmy nierówność Czebyszewa: 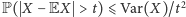dla dowolnego 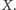Dostajemy więc 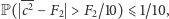czyli wynik wychodzi całkiem niezły.

Przypomnijmy, że nasz algorytm działa w pamięci 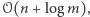a jednak 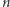czasem może być duże. Liczba 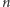bierze się stąd, że przez cały czas przeglądania strumienia pamiętamy 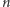zmiennych 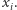Wydaje się to nieuniknione przy tej technice. Okazuje się jednak, że stosunkowo łatwo można zamienić 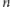na 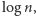używając bardzo pomysłowej metody. Przypomnijmy, jaka własność zmiennych 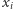była nam potrzebna. Mianowicie chcieliśmy, by 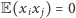dla 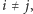czyli by były one parami niezależne. Przy szacowaniu wariancji przydaje się ponadto niezależność czwórkami, dzięki której wiele ze składników postaci 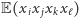znika. Można skonstruować obiekt wielkości 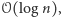z którego można wydobyć zmiennych czwórkami niezależnych. My pokażemy jedynie, że da się tak zrobić dla zmiennych parami niezależnych. Zachęcamy Ambitnego Czytelnika do uogólnienia tego faktu. Dla uproszczenia załóżmy, że 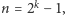w tym przypadku mamy 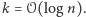Wówczas pamiętamy 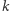niezależnych zmiennych losowych 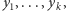takich, że 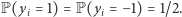Dla dowolnego niepustego podzbioru 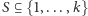definiujemy zmienną 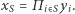Łatwo sprawdzić, że 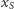i i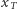stotnie są niezależne dla dwóch różnych zbiorów 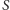i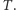

Algorytm obliczający przybliżoną wartość 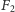został opublikowany w 1999 roku przez Alona (patrz też str. 8), Matiasa i Szegedego jako chyba najbardziej zaskakujący wynik ich przełomowej pracy. Praca ta położyła fundamenty pod bardzo szybko rosnącą dziedzinę algorytmów strumieniowych, a autorzy otrzymali prestiżową nagrodę Gödla.