Chciałoby się wiedzieć coś na pewno, a nie tylko z dużą dozą prawdopodobieństwa. Szczęśliwie okazuje się, że czasami da się tę losowość wprowadzić, a potem wyeliminować. Ta ostatnia operacja, eliminacja losowości, nazywa się derandomizacją.

Przedstawimy dwie metody derandomizacji. Zrobimy to na przykładzie, choć użyte techniki będą zdecydowanie bardziej ogólne. Rozważmy graf 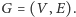Dla podzbioru wierzchołków 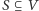nazwiemy jego cięciem zbiór 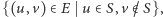czyli zbiór krawędzi, które mają dokładnie jeden koniec w 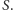Problem znajdowania 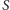o największym cięciu jest NP-zupełny. Rozważmy jednak podobny problem: znajdowania 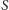takiego, że jego cięcie jest wielkości co najmniej połowy zbioru wszystkich krawędzi, czyli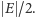

Na pierwszy rzut oka nie jest wcale jasne, czy taki 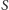istnieje. A więc na rozgrzewkę udowodnijmy to. Zachęcamy Czytelników do samodzielnej próby przed przeczytaniem rozwiązania. Rozwiązanie zaś jest zadziwiająco proste. Wylosujmy 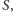to znaczy każdy wierzchołek wrzućmy niezależnie do 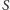z prawdopodobieństwem 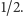Wówczas każda krawędź z 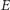będzie należała do cięcia 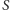z prawdopodobieństwem 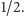A zatem średnia wielkość cięcia 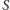to 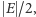czyli na pewno musi istnieć 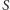taki, że jego cięcie ma wielkość przynajmniej 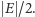Powyższy dowód jest jednak niekonstruktywny, nie wynika z niego wcale, jak takie cięcie znaleźć. Oczywiście, możemy przejrzeć wszystkie możliwe zbiory 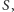ale to zajmie czas rzędu 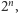gdzie 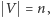a my chcemy znaleźć algorytm wielomianowy względem

Podamy dwie metody. Pierwsza nazywa się metodą warunkowych wartości oczekiwanych. Przypuśćmy, że przejrzeliśmy już pewien zbiór wierzchołków 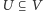i dla każdego z nich zdecydowaliśmy, czy będzie on należał do 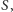czy nie. Jaka jest średnia wielkość cięcia 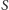po tym ustaleniu? Przez 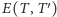oznaczmy zbiór krawędzi między zbioram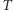i i 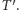Na razie wiemy, że do cięcia na pewno będzie należała każda krawędź z 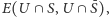gdzie 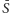to dopełnienie zbioru 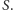Jeśli chodzi o krawędzie jeszcze nieustalone, to każda krawędź z 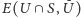będzie należała do cięcia z prawdopodobieństwem 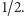A zatem średnia wartość cięcia po ustaleniu, co się stanie z wierzchołkami z 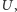wynosi 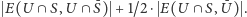Umiemy to obliczyć w czasie wielomianowym, znając 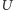oraz decyzję odnośnie 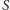na nim, czyli 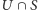oraz 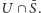Teraz już tylko krok do rozwiązania. Gdy bowiem decydujemy o pierwszym wierzchołku, czy wrzucić go do 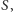czy nie, to obliczamy, jaka będzie średnia wartość cięcia w obu przypadkach. Ponieważ średnia z tych dwóch liczb jest większa lub równa 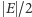(w tym przypadku równa), to jedna z nich też będzie większa lub równa. Wybieramy więc tę lepszą opcję i zabieramy się za drugi element. Przy dorzucaniu każdego nowego elementu wybieramy tę opcję, która daje większą średnią i w ten sposób po podjęciu decyzji dla wszystkich elementów 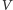otrzymujemy pewien zbiór 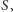którego cięcie będzie większe lub równe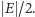

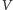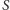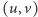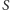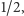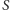Drugie rozwiązanie jest jeszcze bardziej zaskakujące. Zauważmy, że tak naprawdę nie potrzebujemy wcale, by każdy wierzchołek z był brany do niezależnie. Do tego, by każda krawędź znalazła się w cięciu z prawdopodobieństwem wystarczy, by wierzchołki i były wzięte do niezależnie , czyli wystarczy nam, by wybory były parami niezależne. A to jest dużo słabsze wymaganie! Co więcej, okazuje się, że z 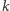niezależnych zmiennych losowych 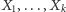o wartościach w 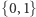można łatwo skonstruować 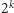zmiennych losowych parami niezależnych o wartościach w 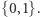Po prostu dla każdego podzbioru 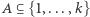zmienna 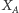jest zdefiniowana jako xor (alternatywa wykluczająca) zmiennych 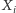takich, że 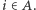Nietrudno zauważyć, że dla dowolnych 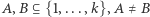zmienne 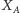i 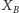są niezależne. Dla uproszczenia przyjmijmy, że 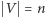jest potęgą dwójki. 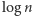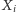A więc nasz algorytm możemy zamienić na taki, który losuje najpierw bitów dla 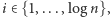a potem gdy podejmuje losową decyzję, czy wrzucić jakiś wierzchołek z 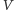do zbioru 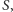korzysta ze zmiennych 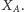Taki algorytm też w średnim przypadku skonstruuje cięcie wielkości 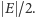Zauważmy jednak, że zamiast losować te 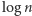wartości możemy po prostu sprawdzić wszystkie możliwości ich wylosowań, których jest 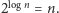Czyli faktycznie otrzymaliśmy wielomianowy algorytm deterministyczny: przegląda on wszystkie możliwości na 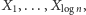dla każdej symuluje działanie losowego algorytmu, a na koniec wybiera najlepsze rozwiązanie.