Informatyczny kącik olimpijski
Przeciąganie liny
W tym miesiącu proponujemy zadanie Przeciąganie liny, które pojawiło się w podwarszawskim Józefowie, podczas zeszłorocznej Bałtyckiej Olimpiady Informatycznej. Zadanie opisuje problem optymalizacji znanej wakacyjno-urlopowej zabawy. Co ciekawe, warstwa fabularna proponowanego rozwiązania - choć pozostaje w podobnych klimatach - to jednak odchodzi od liny na rzecz plecaka.
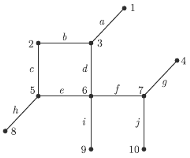
Wierzchołki oznaczono liczbami, krawędzie - literami. Jedyne możliwe przyporządkowania to:
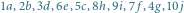 albo
albo
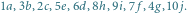
Ale po kolei:
W zadaniu rozważamy 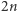 osób chcących zabawić się w tytułową grę. Lina do zabawy ma przygotowane
osób chcących zabawić się w tytułową grę. Lina do zabawy ma przygotowane 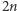 uchwytów, po
uchwytów, po  z każdej strony. Każda z osób deklaruje zawczasu dwa uchwyty, przy których chciałaby się znaleźć. Znamy również siłę każdej z osób, wyrażoną przez liczbę naturalną od
z każdej strony. Każda z osób deklaruje zawczasu dwa uchwyty, przy których chciałaby się znaleźć. Znamy również siłę każdej z osób, wyrażoną przez liczbę naturalną od 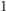 do
do 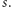 Naszym celem jest ustalić, czy jest możliwe takie ustawienie uczestników zabawy, aby każdy dostał jeden z dwóch wybranych przez siebie uchwytów oraz aby różnica sił między dwiema drużynami nie przekraczała pewnej danej liczby
Naszym celem jest ustalić, czy jest możliwe takie ustawienie uczestników zabawy, aby każdy dostał jeden z dwóch wybranych przez siebie uchwytów oraz aby różnica sił między dwiema drużynami nie przekraczała pewnej danej liczby 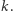
Ograniczenia opisane w zadaniu wydają się dość dziwaczne. Najlepiej jest na nie spojrzeć w następujący sposób. Rozważmy graf 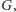 w którym wierzchołki reprezentują uchwyty, a krawędzie - ludzi. Krawędź
w którym wierzchołki reprezentują uchwyty, a krawędzie - ludzi. Krawędź  łączy wierzchołki
łączy wierzchołki  i
i 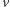 wtedy i tylko wtedy, gdy osoba
wtedy i tylko wtedy, gdy osoba  zadeklarowała jako ulubione właśnie uchwyty
zadeklarowała jako ulubione właśnie uchwyty  i
i 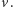 W tym języku przyporządkowanie osobom uchwytów sprowadza się do (wzajemnie jednoznacznego) przyporządkowania krawędziom jednego z ich wierzchołków.
W tym języku przyporządkowanie osobom uchwytów sprowadza się do (wzajemnie jednoznacznego) przyporządkowania krawędziom jednego z ich wierzchołków.
Nawet jeśli zapomnimy o warunku dotyczącym zrównoważenia sił obu stron, nie zawsze jest możliwe jakiekolwiek przyporządkowanie spełniające wszystkie preferencje dotyczące uchwytów. Przede wszystkim, w 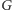 każda spójna składowa o
każda spójna składowa o 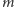 wierzchołkach musi mieć dokładnie
wierzchołkach musi mieć dokładnie 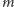 krawędzi. Takie grafy to tak zwane pseudolasy, a więc zbiory rozłącznych pseudodrzew. Każde pseudodrzewo zawiera dokładnie jeden cykl (dlaczego?). W takim grafie istnieją tylko dwa różne przyporządkowania wierzchołków do sąsiednich krawędzi. Dla wierzchołków nie leżących na cyklu możliwy jest tylko jeden wybór. Na cyklu wybory są dwa: przyporządkujemy krawędzie kolejnym wierzchołkom albo zgodnie albo przeciwnie do ruchu wskazówek zegara.
krawędzi. Takie grafy to tak zwane pseudolasy, a więc zbiory rozłącznych pseudodrzew. Każde pseudodrzewo zawiera dokładnie jeden cykl (dlaczego?). W takim grafie istnieją tylko dwa różne przyporządkowania wierzchołków do sąsiednich krawędzi. Dla wierzchołków nie leżących na cyklu możliwy jest tylko jeden wybór. Na cyklu wybory są dwa: przyporządkujemy krawędzie kolejnym wierzchołkom albo zgodnie albo przeciwnie do ruchu wskazówek zegara.
Wobec powyższego, nasze rozwiązanie w pierwszej fazie sprawdza, czy dane wejściowe rzeczywiście tworzą pseudolas. Jeśli nie, to oczywiście odpowiedź na zadanie brzmi również "nie". Dalej zakładamy więc, że mamy do czynienia już tylko z pewnym zbiorem pseudodrzew. Jak zauważyliśmy wcześniej, dla każdego takiego pseudodrzewa mamy tylko dwie możliwości. Dla każdej z nich obliczmy jaką siłę do lewej strony liny wnosi. Te wartości oznaczmy jako 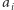 oraz
oraz 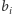 dla
dla 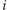 -tego pseudodrzewa. Bez straty ogólności załóżmy, że zawsze
-tego pseudodrzewa. Bez straty ogólności załóżmy, że zawsze 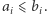 Widzimy, że łączna siła lewej drużyny będzie równa co najmniej
Widzimy, że łączna siła lewej drużyny będzie równa co najmniej 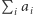 i co najwyżej
i co najwyżej 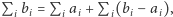 przy czym każdy ze składników
przy czym każdy ze składników 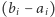 możemy dodać bądź nie, według naszego uznania. Pamiętajmy oczywiście, że chcemy, aby ta siła mieściła się między
możemy dodać bądź nie, według naszego uznania. Pamiętajmy oczywiście, że chcemy, aby ta siła mieściła się między 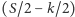 a
a 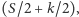 gdzie
gdzie 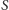 oznacza łączną siłę wszystkich osób.
oznacza łączną siłę wszystkich osób.
To ostatnie spojrzenie na problem z zadania opiszemy w języku tak zwanego problemu plecakowego (ang. knapsack problem). Rozważmy plecak o pojemności maksymalnej 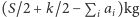 . Mamy dostępny zbiór przedmiotów (indeksowany
. Mamy dostępny zbiór przedmiotów (indeksowany 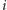 ) o wagach
) o wagach 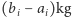 . Pytamy, czy uda się nam zabrać przedmioty o łącznej wadze co najmniej
. Pytamy, czy uda się nam zabrać przedmioty o łącznej wadze co najmniej 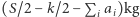 i jednocześnie nieprzekraczającej pojemności plecaka.
i jednocześnie nieprzekraczającej pojemności plecaka.
Problem plecakowy to klasyczny problem, który da się standardowo rozwiązać w czasie 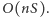 W naszym zadaniu możemy jednak znaleźć rozwiązania lepsze (o ile
W naszym zadaniu możemy jednak znaleźć rozwiązania lepsze (o ile 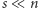 ), bo działające w czasie
), bo działające w czasie 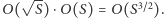
Skorzystamy z założenia, że siła każdej osoby (a więc i wagi przedmiotów w problemie plecakowym) jest wyrażona liczbą naturalną. Wnioskujemy z tego, że istnieje co najwyżej 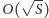 różnych wartości wag przedmiotów (suma
różnych wartości wag przedmiotów (suma 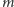 różnych liczb naturalnych jest równa co najmniej
różnych liczb naturalnych jest równa co najmniej 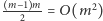 ). Pozostaje ostatni krok, zrealizowany za pomocą programowania dynamicznego:
). Pozostaje ostatni krok, zrealizowany za pomocą programowania dynamicznego:
Tworzymy (początkowo wypełnioną zerami) binarną tablicę 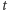 rozmiaru
rozmiaru 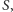 w której będziemy zaznaczać, czy da się przygotować plecak o ustalonej wadze. Działamy w pętli o
w której będziemy zaznaczać, czy da się przygotować plecak o ustalonej wadze. Działamy w pętli o 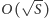 obrotach, w każdym obrocie dając dostęp do kolejnej unikatowej wagi przedmiotu.
obrotach, w każdym obrocie dając dostęp do kolejnej unikatowej wagi przedmiotu.
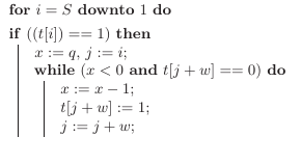
Oto pseudokod jednego obrotu, dla nowej wagi 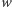 występującej
występującej 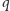 razy:
razy:
W każdym kroku pętli albo uzyskujemy nową objętość plecaka albo kończymy dodawania dla ustalonej objętości. Oba zdarzenia mogą wystąpić 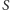 razy, stąd czas działania jednego obrotu pętli to faktycznie
razy, stąd czas działania jednego obrotu pętli to faktycznie 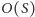 tak, jak zapowiedzieliśmy.
tak, jak zapowiedzieliśmy.
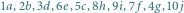 albo
albo