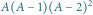Informatyczny kącik olimpijski
Równoważność palindromiczna (100)
W jubileuszowym odcinku kącika omówimy zadanie Równoważność palindromiczna, które pojawiło się na Obozie Naukowo-Treningowym im. A. Kreczmara w 2010 roku.
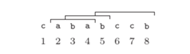
Rys. 1 W 8-literowym słowie 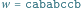 na pozycji
na pozycji 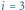 występuje palindrom nieparzysty aba o długości
występuje palindrom nieparzysty aba o długości 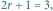 gdyż
gdyż 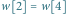 oraz
oraz 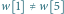
Dwa słowa 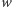 i
i  o długości
o długości  nazwiemy równoważnymi palindromicznie, jeśli dla każdej pary liczb
nazwiemy równoważnymi palindromicznie, jeśli dla każdej pary liczb 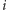 oraz
oraz 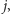 takich że
takich że 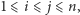 podsłowo
podsłowo ![| w[i..j]](/math/temat/informatyka/algorytmy/2016/11/26/Rownowaznosc_palindromiczna/7x-6171d30ae8b5a8fa0b97be10cb10e51e93749716-im-33,33,33-FF,FF,FF.gif) złożone z liter na pozycjach od
złożone z liter na pozycjach od 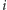 -tej do
-tej do 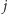 -tej jest palindromem wtedy i tylko wtedy, gdy palindromem jest podsłowo
-tej jest palindromem wtedy i tylko wtedy, gdy palindromem jest podsłowo ![|v[i.. j]](/math/temat/informatyka/algorytmy/2016/11/26/Rownowaznosc_palindromiczna/10x-6171d30ae8b5a8fa0b97be10cb10e51e93749716-im-33,33,33-FF,FF,FF.gif) złożone z liter na tych samych pozycjach. Mając dane słowo
złożone z liter na tych samych pozycjach. Mając dane słowo 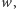 należy wyznaczyć liczbę słów równoważnych mu palindromicznie, zawierających litery z ustalonego
należy wyznaczyć liczbę słów równoważnych mu palindromicznie, zawierających litery z ustalonego 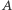 -literowego alfabetu.
-literowego alfabetu.
Rozważmy pewien palindrom 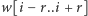 o nieparzystej długości
o nieparzystej długości 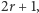 którego środek jest na pozycji
którego środek jest na pozycji 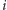 w słowie
w słowie 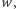 oraz który nie może być rozszerzony (tzn. nie istnieje dłuższy palindrom o tym samym środku). Zatem w słowie
oraz który nie może być rozszerzony (tzn. nie istnieje dłuższy palindrom o tym samym środku). Zatem w słowie  także musi istnieć analogiczny palindrom, zatem muszą być spełnione równości liter
także musi istnieć analogiczny palindrom, zatem muszą być spełnione równości liter ![|v[i− k] = v[i + k]](/math/temat/informatyka/algorytmy/2016/11/26/Rownowaznosc_palindromiczna/6x-75d297071a3c2bff58feda1862eb7da8443dad0e-im-33,33,33-FF,FF,FF.gif) dla
dla 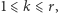 oraz nierówność
oraz nierówność ![| v[i −r − 1] ≠ v[i + r+ 1].](/math/temat/informatyka/algorytmy/2016/11/26/Rownowaznosc_palindromiczna/8x-75d297071a3c2bff58feda1862eb7da8443dad0e-im-33,33,33-FF,FF,FF.gif) Nietrudno się przekonać, że zbiór takich (nie)równości dla wszystkich pozycji
Nietrudno się przekonać, że zbiór takich (nie)równości dla wszystkich pozycji 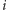 (wraz z analogicznym zbiorem dla palindromów o parzystej długości) w pełni opisuje warunki, jakie musi spełniać słowo
(wraz z analogicznym zbiorem dla palindromów o parzystej długości) w pełni opisuje warunki, jakie musi spełniać słowo 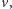 aby być palindromicznie równoważnym słowu
aby być palindromicznie równoważnym słowu 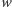 (patrz Rys. 1).
(patrz Rys. 1).
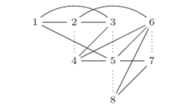
Rys. 2 Graf 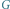 odpowiadający słowu
odpowiadający słowu 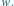 Wierzchołki 2 i 4 są w tej samej składowej grafu
Wierzchołki 2 i 4 są w tej samej składowej grafu 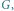 zaś wierzchołki 1 i 5 są połączone krawędzią ciągłą
zaś wierzchołki 1 i 5 są połączone krawędzią ciągłą
Zbiór ten możemy przedstawić jako graf 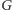 o wierzchołkach
o wierzchołkach 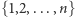 odpowiadających pozycjom w słowie
odpowiadających pozycjom w słowie 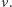 Krawędź łącząca dwa wierzchołki będzie przerywana, jeśli odpowiadające im pozycje w słowie muszą mieć tę samą literę, lub ciągła, jeśli muszą mieć różne litery. W ten sposób sprowadzimy nasze zadanie do problemu kolorowania grafu: liczba słów palindromicznie równoważnych słowu
Krawędź łącząca dwa wierzchołki będzie przerywana, jeśli odpowiadające im pozycje w słowie muszą mieć tę samą literę, lub ciągła, jeśli muszą mieć różne litery. W ten sposób sprowadzimy nasze zadanie do problemu kolorowania grafu: liczba słów palindromicznie równoważnych słowu 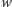 jest bowiem równa liczbie kolorowań grafu
jest bowiem równa liczbie kolorowań grafu 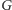 przy pomocy
przy pomocy 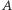 kolorów (przy zachowaniu ograniczeń na wynikających z istnienia krawędzi ciągłych i przerywanych; Rys. 2).
kolorów (przy zachowaniu ograniczeń na wynikających z istnienia krawędzi ciągłych i przerywanych; Rys. 2).
Niestety, nie znamy wielomianowego algorytmu dla ogólnego problemu zliczania kolorowań grafów, będziemy musieli więc nieco bliżej przyjrzeć się szczególnej postaci grafu z zadania. Na początek pozbędziemy się krawędzi przerywanych, scalając łączone przez nie wierzchołki. Powiemy, że dwa wierzchołki 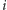 oraz
oraz 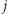 należą do tej samej składowej w grafie
należą do tej samej składowej w grafie 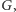 jeśli są połączone przerywaną ścieżką. Każdą składową zastępujemy pojedynczym wierzchołkiem (o numerze będącym najmniejszym numerem wierzchołka z tej składowej), do którego wchodzą wszystkie krawędzie ciągłe poprzednio wchodzące do wierzchołków tej składowej.
jeśli są połączone przerywaną ścieżką. Każdą składową zastępujemy pojedynczym wierzchołkiem (o numerze będącym najmniejszym numerem wierzchołka z tej składowej), do którego wchodzą wszystkie krawędzie ciągłe poprzednio wchodzące do wierzchołków tej składowej.
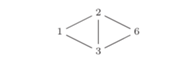
Rys. 3 Graf 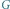 po zastąpieniu składowych pojedynczymi wierzchołkami. Liczba kolorowań tego grafu to
po zastąpieniu składowych pojedynczymi wierzchołkami. Liczba kolorowań tego grafu to 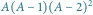
W tak uzyskanym grafie będziemy zachłannie kolorować wierzchołki w kolejności rosnących numerów. Załóżmy, że chcemy pokolorować wierzchołek 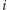 oraz że jest on połączony krawędziami ciągłymi z wierzchołkami o mniejszych numerach
oraz że jest on połączony krawędziami ciągłymi z wierzchołkami o mniejszych numerach 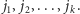 Kluczową własnością grafu, która umożliwi nam kolorowanie zachłanne jest to, że każda para wierzchołków spośród
Kluczową własnością grafu, która umożliwi nam kolorowanie zachłanne jest to, że każda para wierzchołków spośród 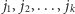 jest również połączona krawędzią ciągłą, czyli wszystkie one muszą mieć różne kolory, zatem wierzchołek
jest również połączona krawędzią ciągłą, czyli wszystkie one muszą mieć różne kolory, zatem wierzchołek 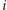 możemy pokolorować na
możemy pokolorować na 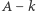 sposobów, niezależnie od kolorowania wierzchołków o mniejszych numerach (Rys. 3).
sposobów, niezależnie od kolorowania wierzchołków o mniejszych numerach (Rys. 3).
Dowód kluczowej własności jest nieco techniczny i wymaga przyjrzeniu się, jak mogą być położone palindromy w słowie 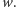 Powiemy, że dwa wierzchołki
Powiemy, że dwa wierzchołki 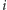 oraz
oraz 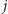 są sąsiednie, jeśli należą do tej samej składowej,
są sąsiednie, jeśli należą do tej samej składowej, 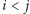 oraz nie istnieje
oraz nie istnieje 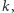 że
że 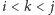 i
i 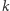 też należy do tej samej składowej. Dowód można przeprowadzić, udowadniając następujące własności:
też należy do tej samej składowej. Dowód można przeprowadzić, udowadniając następujące własności:
- Jeśli
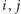 są sąsiednie, to
są sąsiednie, to ![w[i..j]](/math/temat/informatyka/algorytmy/2016/11/26/Rownowaznosc_palindromiczna/10x-00329d8642f8d7e653bace2144ab987d600d40e6-im-33,33,33-FF,FF,FF.gif) jest palindromem.
jest palindromem. - Jeśli
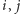 są sąsiednie,
są sąsiednie, 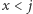 oraz
oraz  i
i 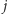 są połączone krawędzią ciągłą, to
są połączone krawędzią ciągłą, to 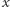 i
i 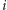 też są połączone krawędzią ciągłą (wynika z tego, że dla danej składowej wystarczy rozważać krawędzie ciągłe wchodzące do jednego wierzchołka z tej składowej - tego o najmniejszym numerze).
też są połączone krawędzią ciągłą (wynika z tego, że dla danej składowej wystarczy rozważać krawędzie ciągłe wchodzące do jednego wierzchołka z tej składowej - tego o najmniejszym numerze). - Jeśli
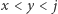 i
i 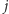 jest wierzchołkiem o najmniejszym numerze ze swojej składowej oraz
jest wierzchołkiem o najmniejszym numerze ze swojej składowej oraz 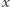 i
i 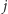 są połączone krawędzią ciągłą oraz
są połączone krawędzią ciągłą oraz 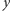 i
i 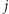 są połączone krawędzią ciągłą, to istnieje taki wierzchołek
są połączone krawędzią ciągłą, to istnieje taki wierzchołek 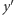 ze składowej wierzchołka
ze składowej wierzchołka 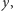 że
że  i
i 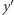 są też połączone krawędzią ciągłą.
są też połączone krawędzią ciągłą.
Pozostaje oszacować efektywność powyższego algorytmu. Zbiór (nie)równości konstruowanych na podstawie słowa 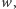 a które odpowiadają krawędziom grafu
a które odpowiadają krawędziom grafu 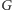 może mieć rozmiar
może mieć rozmiar 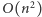 i taka też będzie złożoność czasowa i pamięciowa powyższego algorytmu. Zauważmy jednak, że nierówności (czyli krawędzi ciągłych) jest jedynie
i taka też będzie złożoność czasowa i pamięciowa powyższego algorytmu. Zauważmy jednak, że nierówności (czyli krawędzi ciągłych) jest jedynie 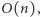 pozostałe to równości, czyli krawędzie przerywane, służące do wyznaczenie składowych grafu. Czytelnikom Dociekliwym polecamy zastanowić się, jak można wykorzystać algorytm Manachera znajdowania palindromów w słowie, do zmniejszenia liczby rozważanych krawędzi przerywanych do liniowej.
pozostałe to równości, czyli krawędzie przerywane, służące do wyznaczenie składowych grafu. Czytelnikom Dociekliwym polecamy zastanowić się, jak można wykorzystać algorytm Manachera znajdowania palindromów w słowie, do zmniejszenia liczby rozważanych krawędzi przerywanych do liniowej.
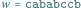 na pozycji
na pozycji 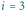 występuje palindrom nieparzysty aba o długości
występuje palindrom nieparzysty aba o długości 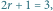 gdyż
gdyż 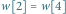 oraz
oraz 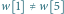
 odpowiadający słowu
odpowiadający słowu 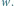 Wierzchołki 2 i 4 są w tej samej składowej grafu
Wierzchołki 2 i 4 są w tej samej składowej grafu 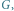 zaś wierzchołki 1 i 5 są połączone krawędzią ciągłą
zaś wierzchołki 1 i 5 są połączone krawędzią ciągłą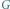 po zastąpieniu składowych pojedynczymi wierzchołkami. Liczba kolorowań tego grafu to
po zastąpieniu składowych pojedynczymi wierzchołkami. Liczba kolorowań tego grafu to