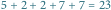Informatyczny kącik olimpijski
Oblodzone drogi
W tym miesiącu omówimy zadanie Icy Roads z obozu w Petrozawodsku z roku 2013.
Rys. 1 Przykładowa sieć dla 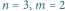 o czasach przejazdu
o czasach przejazdu 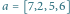 i
i 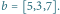 Optymalna trasa o czasie
Optymalna trasa o czasie 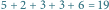 została przedstawiona kolorowymi strzałkami. Zauważmy, że na skrzyżowaniu
została przedstawiona kolorowymi strzałkami. Zauważmy, że na skrzyżowaniu 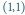 wybrany został odcinek alei o czasie przejazdu 3, zamiast ulicy o czasie przejazdu 2. Algorytm zachłanny (strzałki przerywane) znalazłby trasę o czasie
wybrany został odcinek alei o czasie przejazdu 3, zamiast ulicy o czasie przejazdu 2. Algorytm zachłanny (strzałki przerywane) znalazłby trasę o czasie 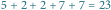
Zadanie. Sieć drogowa w mieście składa się z 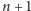 pionowych ulic oraz
pionowych ulic oraz 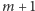 poziomych alei. Chcemy jak najszybciej dostać się ze skrzyżowania
poziomych alei. Chcemy jak najszybciej dostać się ze skrzyżowania 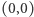 do skrzyżowania
do skrzyżowania 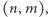 pokonując
pokonując 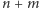 odcinków dróg. Niestety, drogi są oblodzone i jeździ się po nich dość wolno: przejechanie jednego odcinka
odcinków dróg. Niestety, drogi są oblodzone i jeździ się po nich dość wolno: przejechanie jednego odcinka 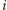 -tej ulicy zajmuje czas
-tej ulicy zajmuje czas 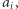 zaś przejechanie jednego odcinka
zaś przejechanie jednego odcinka 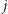 -tej alei zajmuje czas
-tej alei zajmuje czas 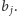 Należy wyznaczyć najszybszą trasę przejazdu.
Należy wyznaczyć najszybszą trasę przejazdu.
Na rysunku 1 przedstawiono przykładową sieć i wyjaśniono, dlaczego algorytm zachłanny, który na każdym kolejnym skrzyżowaniu wybiera tę ulicę/aleję, która ma mniejszy czas przejazdu, nie jest poprawny.
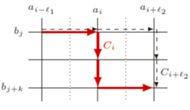
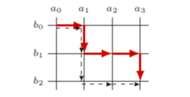
Rys. 2 Ilustracja do dowodu, że przy pewnych założeniach możemy zablokować ulicę 
Pomimo prostego sformułowania, zadanie jest trudne i wymaga kilku pomysłowych obserwacji. Główna idea rozwiązania będzie opierać się na sukcesywnym blokowaniu tych ulicąlei, którymi nie opłaca się jeździć. Na początek pokażemy, że jeśli jakaś ulica 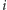 znajduje się pomiędzy dwiema ulicami o mniejszych czasach przejazdu, to można ją zablokować. Załóżmy, że w pewnym optymalnym rozwiązaniu przejeżdżamy odcinkami tej ulicy pomiędzy alejami
znajduje się pomiędzy dwiema ulicami o mniejszych czasach przejazdu, to można ją zablokować. Załóżmy, że w pewnym optymalnym rozwiązaniu przejeżdżamy odcinkami tej ulicy pomiędzy alejami 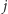 oraz
oraz 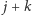 (Rys. 2). Niech
(Rys. 2). Niech 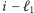 oraz
oraz 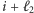 będą numerami tych niezablokowanych jeszcze ulic, pomiędzy którymi znajduje się ulica
będą numerami tych niezablokowanych jeszcze ulic, pomiędzy którymi znajduje się ulica 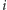 (przy pierwszym czytaniu można przyjąć
(przy pierwszym czytaniu można przyjąć 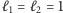 ). Zgodnie z założeniem mamy
). Zgodnie z założeniem mamy 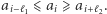 Czas przejazdu wynosi
Czas przejazdu wynosi 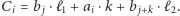 Natomiast czasy przejazdu, gdybyśmy zamiast ulicy
Natomiast czasy przejazdu, gdybyśmy zamiast ulicy 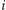 wybrali ulicę
wybrali ulicę 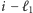 lub
lub 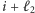 wynoszą odpowiednio
wynoszą odpowiednio 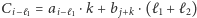 oraz
oraz 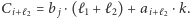 Widać jednak, że co najmniej jedna z tych tras ma czas nie większy niż optymalny:
Widać jednak, że co najmniej jedna z tych tras ma czas nie większy niż optymalny:
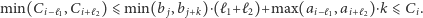 |
Powtarzając powyższe rozumowanie, możemy zablokować część ulic w mieście tak, że czasy przejazdu pozostałych będą tworzyć ciąg unimodalny (najpierw będą maleć, osiągając minimum na pewnej ulicy 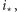 a potem rosnąć). Zauważmy, że blokowanie ulic powoduje, że odległości między kolejnymi niezablokowanymi ulicami mogą się zwiększać (stąd konieczność uwzględnienia wartości
a potem rosnąć). Zauważmy, że blokowanie ulic powoduje, że odległości między kolejnymi niezablokowanymi ulicami mogą się zwiększać (stąd konieczność uwzględnienia wartości 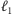 i
i 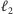 w powyższym dowodzie). Cały argument możemy niezależnie zastosować do alei (które zatem też będą tworzyć ciąg unimodalny, osiągając minimum na pewnej alei
w powyższym dowodzie). Cały argument możemy niezależnie zastosować do alei (które zatem też będą tworzyć ciąg unimodalny, osiągając minimum na pewnej alei 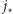 ). Druga obserwacja jest następująca: optymalna trasa będzie przechodziła przez skrzyżowanie
). Druga obserwacja jest następująca: optymalna trasa będzie przechodziła przez skrzyżowanie 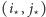 najtańszej ulicy z najtańszą aleją. (Jeśli tak nie jest, to rozważamy punkt przecięcia trasy z ulicą
najtańszej ulicy z najtańszą aleją. (Jeśli tak nie jest, to rozważamy punkt przecięcia trasy z ulicą 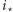 oraz punkt przecięcia trasy z aleją
oraz punkt przecięcia trasy z aleją 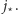 Przejście pomiędzy tymi punktami po odcinkach ulicy
Przejście pomiędzy tymi punktami po odcinkach ulicy 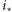 oraz alei
oraz alei 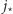 nie pogorszy rozwiązania.) Zatem możemy nasz problem podzielić na dwa niezależne problemy szukania trasy ze skrzyżowania
nie pogorszy rozwiązania.) Zatem możemy nasz problem podzielić na dwa niezależne problemy szukania trasy ze skrzyżowania 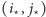 do skrzyżowania
do skrzyżowania 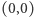 oraz trasy ze skrzyżowania
oraz trasy ze skrzyżowania 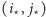 do skrzyżowania
do skrzyżowania 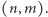 Bez straty ogólności możemy więc założyć, że ciągi
Bez straty ogólności możemy więc założyć, że ciągi 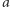 i
i 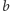 czasów przejazdu dla niezablokowanych ulic i alei są rosnące.
czasów przejazdu dla niezablokowanych ulic i alei są rosnące.
Pójdziemy jeszcze krok dalej i pokażemy silniejszy warunek na te ciągi, a mianowicie, że funkcje 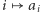 oraz
oraz 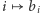 dla niezablokowanych ulicąlei są wypukłe. Przez
dla niezablokowanych ulicąlei są wypukłe. Przez 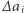 oznaczmy średni przyrost czasu na odcinek od ulicy
oznaczmy średni przyrost czasu na odcinek od ulicy 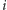 do następnej niezablokowanej ulicy (analogicznie
do następnej niezablokowanej ulicy (analogicznie 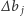 dla alei). Zatem dla rysunku 2 mamy (przy dodatkowym założeniu, że aleje
dla alei). Zatem dla rysunku 2 mamy (przy dodatkowym założeniu, że aleje 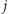 i
i 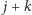 są sąsiednie):
są sąsiednie):
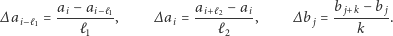 |
Ponownie rozpisując wzory na czasy przejazdu trasami 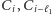 i
i 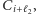 dostajemy, że
dostajemy, że
 |
Jeśli 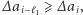 to co najmniej jeden z powyższych warunków jest spełniony, więc
to co najmniej jeden z powyższych warunków jest spełniony, więc 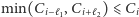 i można zablokować
i można zablokować 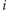 -tą ulicę. Powtarzając to rozumowanie, powodujemy w końcu, że ciągi
-tą ulicę. Powtarzając to rozumowanie, powodujemy w końcu, że ciągi 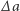 oraz
oraz 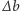 dla niezablokowanych ulicąlei są rosnące.
dla niezablokowanych ulicąlei są rosnące.
Rys. 3 Ilustracja działania algorytmu zachłannego
Pora na ostatnią obserwację: na tak poblokowanej sieci drogowej możemy już stosować algorytm zachłanny, tzn. na każdym skrzyżowaniu wybierać tę ulicęąleję, która ma mniejszy współczynnik średniego przyrostu czasu. A konkretnie: będąc na skrzyżowaniu  -tej ulicy z
-tej ulicy z  -tą aleją wybieramy ulicę, jeśli
-tą aleją wybieramy ulicę, jeśli 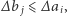 a aleję, jeśli
a aleję, jeśli 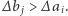 Dowód poprawności tego algorytmu przeprowadzimy przez indukcję po
Dowód poprawności tego algorytmu przeprowadzimy przez indukcję po 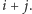 Dla
Dla 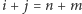 teza jest oczywista (jesteśmy na ostatnim skrzyżowaniu i nie mamy co wybierać). Załóżmy zatem, że algorytm zachłanny działa poprawnie, jeśli startujemy z dowolnego skrzyżowania
teza jest oczywista (jesteśmy na ostatnim skrzyżowaniu i nie mamy co wybierać). Załóżmy zatem, że algorytm zachłanny działa poprawnie, jeśli startujemy z dowolnego skrzyżowania 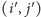 dla którego
dla którego 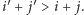 Ponadto załóżmy (Rys. 3), że jest spełnione
Ponadto załóżmy (Rys. 3), że jest spełnione 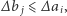 ale w rozwiązaniu optymalnym wybieramy aleję, zatem jedziemy do skrzyżowania
ale w rozwiązaniu optymalnym wybieramy aleję, zatem jedziemy do skrzyżowania 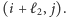 Z wypukłości mamy
Z wypukłości mamy 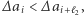 zatem tym bardziej jest spełnione
zatem tym bardziej jest spełnione 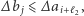 więc z założenia indukcyjnego wynika, że w drugim ruchu wybierzemy ulicę, przesuwając się do skrzyżowania
więc z założenia indukcyjnego wynika, że w drugim ruchu wybierzemy ulicę, przesuwając się do skrzyżowania 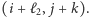 Te dwa ruchy kosztowały nas czas
Te dwa ruchy kosztowały nas czas 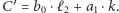 Jednakże rozwiązanie, w którym dostajemy się do skrzyżowania
Jednakże rozwiązanie, w którym dostajemy się do skrzyżowania 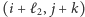 najpierw jadąc ulicą, a potem aleją, ma czas
najpierw jadąc ulicą, a potem aleją, ma czas 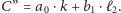 Nietrudno się przekonać, że warunek
Nietrudno się przekonać, że warunek 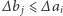 jest równoważny temu, że
jest równoważny temu, że 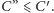 To pokazuje, że istnieje optymalne rozwiązanie, w którym pierwszym ruchem jest wybór ulicy, co kończy dowód.
To pokazuje, że istnieje optymalne rozwiązanie, w którym pierwszym ruchem jest wybór ulicy, co kończy dowód.
Myślę, że Czytelnicy, którzy przebrnęli przez powyższy opis algorytmu nie będą mieli trudności, by zaimplementować go w optymalnej złożoności czasowej 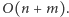
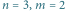 o czasach przejazdu
o czasach przejazdu 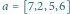 i
i 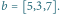 Optymalna trasa o czasie
Optymalna trasa o czasie 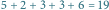 została przedstawiona kolorowymi strzałkami. Zauważmy, że na skrzyżowaniu
została przedstawiona kolorowymi strzałkami. Zauważmy, że na skrzyżowaniu  wybrany został odcinek alei o czasie przejazdu 3, zamiast ulicy o czasie przejazdu 2. Algorytm zachłanny (strzałki przerywane) znalazłby trasę o czasie
wybrany został odcinek alei o czasie przejazdu 3, zamiast ulicy o czasie przejazdu 2. Algorytm zachłanny (strzałki przerywane) znalazłby trasę o czasie