Sortowanie przez kopcowanie
W tym artykule zakładam, że Czytelnik choć trochę programował. W szczególności zna podstawy jakiegoś języka programowania, np. Pascala. Jeśli to podstawowe założenie jest spełnione, to - jestem o tym przekonany - mogę śmiało założyć, że jest mu znane również pojęcie tablicy...
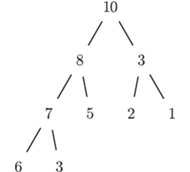
Rys. 1 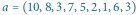
Tablica to bardzo wygodny sposób reprezentowania w programie ciągu zmiennych. Na potrzeby tego artykułu niektóre takie tablice (czyli reprezentowane przez nie ciągi) będziemy uważać za lepsze od innych. Wyróżnione tablice będziemy nazywać tablicami kopcowymi. Aby na taki tytuł zasłużyć, muszą spełniać następujący warunek: elementy tablicy zapisane na kartce w kolejnych wierszach pełnego drzewa binarnego (tytułowego kopca) muszą zachować porządek starszeństwa, tzn. zawsze rodzic musi mieć wartość większą bądź równą swoim dzieciom. Przykład takiej tablicy znajduje się na rysunku 1 Nietrudno zauważyć, że powyższy warunek na "kopcowatość" tablicy ![a[1...n]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/1x-5ac61a6cfbf7c68af03a9896c7e5d6e2931221fe-im-33,33,33-FF,FF,FF.gif) daje się opisać algebraicznie: zawsze
daje się opisać algebraicznie: zawsze ![|a[i]⩾ a[2i]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/2x-5ac61a6cfbf7c68af03a9896c7e5d6e2931221fe-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![a[i] ⩾ a[2i + 1],](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/3x-5ac61a6cfbf7c68af03a9896c7e5d6e2931221fe-im-33,33,33-FF,FF,FF.gif) o ile tylko indeksy mieszczą się w zakresie
o ile tylko indeksy mieszczą się w zakresie 
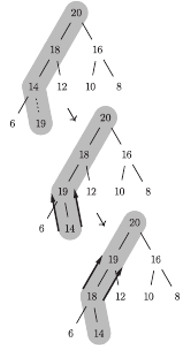
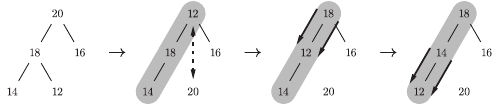
Rys. 2 Schemat działania insert(19) dla 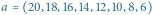
Przedstawiliśmy już głównego bohatera, teraz czas na fabułę. Chcemy sortować. To znaczy: poprzestawiać elementy danej (dowolnej, niekoniecznie kopcowej) tablicy tak, aby tworzyły ciąg niemalejący. Zadanie wykonamy w dwóch fazach. Najpierw pomieszamy elementy, aby utworzyły tablicę kopcową. Dopiero wówczas, w fazie drugiej, zajmiemy się sortowaniem właściwym. Pełny kod naszego rozwiązania reprezentują trzy procedury: sortowanie, insert, deletemax, które podajemy zapisane w języku Pascal. Na pierwszy rzut oka mogą one wydawać się dość skomplikowane. Mam jednak nadzieję, że poniższe intuicje pozwolą zrozumieć, jak dokładnie działa nasz program.
Faza pierwsza realizowana jest za pomocą pętli. Po jej 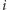 -tym obrocie podtablica
-tym obrocie podtablica ![|a[1...i]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/2x-04df95fac7ca89311b3f8f0e1c5a2bad1cef5f03-im-33,33,33-FF,FF,FF.gif) jest zawsze tablicą kopcową! Żeby się o tym przekonać, dokładnie przemyśl działanie procedury insert. Idea jest bardzo prosta: powiększamy aktualną tablicę kopcową o jeden element, po czym poprawiamy drzewo binarne, analizując ścieżkę drzewa od nowego elementu
jest zawsze tablicą kopcową! Żeby się o tym przekonać, dokładnie przemyśl działanie procedury insert. Idea jest bardzo prosta: powiększamy aktualną tablicę kopcową o jeden element, po czym poprawiamy drzewo binarne, analizując ścieżkę drzewa od nowego elementu ![a[i]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/3x-04df95fac7ca89311b3f8f0e1c5a2bad1cef5f03-im-33,33,33-FF,FF,FF.gif) do korzenia
do korzenia ![a[1].](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/4x-04df95fac7ca89311b3f8f0e1c5a2bad1cef5f03-im-33,33,33-FF,FF,FF.gif) Rysunek 2 powinien być pomocny.
Rysunek 2 powinien być pomocny.
Faza druga jest trochę podobna. Ponownie najważniejsza jest pętla i następujący niezmiennik: gdy indeks pętli jest równy 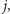 to podtablica
to podtablica ![a[1 ... j]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/2x-00fa84ddc30b871800290eb62ec51a779913e69e-im-33,33,33-FF,FF,FF.gif) jest tablicą kopcową, a elementy
jest tablicą kopcową, a elementy ![a[ j +1...n]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/3x-00fa84ddc30b871800290eb62ec51a779913e69e-im-33,33,33-FF,FF,FF.gif) są poprawnie posortowane. Aby w to uwierzyć, trzeba oczywiście przeanalizować działanie procedury deletemax. Jej zadaniem jest zamienić największy element tablicy kopcowej (czyli zawsze
są poprawnie posortowane. Aby w to uwierzyć, trzeba oczywiście przeanalizować działanie procedury deletemax. Jej zadaniem jest zamienić największy element tablicy kopcowej (czyli zawsze ![a[1]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/4x-00fa84ddc30b871800290eb62ec51a779913e69e-im-33,33,33-FF,FF,FF.gif) ) z ostatnim (czyli
) z ostatnim (czyli ![a[m]](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/5x-00fa84ddc30b871800290eb62ec51a779913e69e-im-33,33,33-FF,FF,FF.gif) ) oraz poprawienie (rysunek 3) reszty tak, aby wciąż stanowiła tablicę kopcową (choć o jeden element krótszą).
) oraz poprawienie (rysunek 3) reszty tak, aby wciąż stanowiła tablicę kopcową (choć o jeden element krótszą).
Powyższy algorytm ma dwie bardzo pozytywne cechy. Po pierwsze: jest bardzo szybki. Każde pojedyncze wywołanie procedury insert czy deletemax zajmuje czas 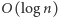 (dlaczego?), a więc łączny czas działania sortowania przez kopcowanie to
(dlaczego?), a więc łączny czas działania sortowania przez kopcowanie to 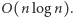 Przy pewnych rozsądnych założeniach da się udowodnić, że to optymalny wynik. (Większość narzucających się prostych rozwiązań działa w czasie
Przy pewnych rozsądnych założeniach da się udowodnić, że to optymalny wynik. (Większość narzucających się prostych rozwiązań działa w czasie 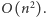 ) Drugą zaletą prezentowanego algorytmu jest złożoność pamięciowa. Poza danymi wejściowymi (tablicą
) Drugą zaletą prezentowanego algorytmu jest złożoność pamięciowa. Poza danymi wejściowymi (tablicą  ) potrzebujemy ledwie kilku dodatkowych zmiennych lokalnych. Stąd mówi się czasem, że sortowanie przez kopcowanie działa w miejscu.
) potrzebujemy ledwie kilku dodatkowych zmiennych lokalnych. Stąd mówi się czasem, że sortowanie przez kopcowanie działa w miejscu.
Rys. 3 Schemat działania deletemax dla 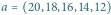
Poza samym zaprezentowanym (dość szybkim i eleganckim) algorytmem chciałbym zwrócić uwagę Czytelnika na pewną ideę, która za nim stoi. Myślę tu o idei abstrakcyjnych struktur danych. Przykładem takiej struktury jest właśnie kopiec. Z lotu ptaka o kopcu (tablicy kopcowej) można myśleć jak o takim wirtualnym czarnym pudełku, o zawartości którego wcale nie musimy zbyt wiele wiedzieć. Pomyślmy o sytuacji, w której nie chciało nam się analizować działania procedur insert oraz deletemax. Wiemy tylko, że pierwsza z nich dokłada element do czarnego pudełka, a druga - wyciąga największy. Dodatkowo poinformowano nas, że obie działają szybko (w czasie proporcjonalnym do logarytmu z liczby elementów w pudełku). To już wystarczy do zrealizowania nie tylko sortowania w czasie 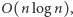 ale i napisania np. programu do obsługi harmonogramu zadań, w którym nieustannie pojawiają się nowe pozycje, z różnymi priorytetami, a komputer decyduje, czym się w danej chwili zająć. Takie myślenie (zapominamy o wnętrzu struktury danych i tylko patrzymy na jej funkcjonalność) nazywamy abstrahowaniem i ono jest absolutnie solą całej algorytmiki. Nie bez powodu większość kursów i podręczników algorytmiki nosi tytuł "Algorytmy i struktury danych".
ale i napisania np. programu do obsługi harmonogramu zadań, w którym nieustannie pojawiają się nowe pozycje, z różnymi priorytetami, a komputer decyduje, czym się w danej chwili zająć. Takie myślenie (zapominamy o wnętrzu struktury danych i tylko patrzymy na jej funkcjonalność) nazywamy abstrahowaniem i ono jest absolutnie solą całej algorytmiki. Nie bez powodu większość kursów i podręczników algorytmiki nosi tytuł "Algorytmy i struktury danych".

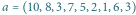
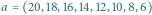
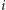 są te o indeksach
są te o indeksach 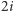 oraz
oraz 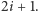 W drugą stronę: dla wierzchołka o indeksie
W drugą stronę: dla wierzchołka o indeksie 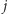 jego rodzic ma indeks
jego rodzic ma indeks 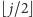 (pascalowo j div 2).
(pascalowo j div 2).![a[1...n].](/math/temat/informatyka/algorytmy/2016/06/22/Sortowanie_przez_kopcowanie/1x-9b4d5e50878bfb9cf76a86621e6b54940f48a4ae-im-33,33,33-FF,FF,FF.gif) Używamy też pomocniczej zmiennej globalnej
Używamy też pomocniczej zmiennej globalnej 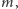 której wartość mówi, jak długi prefiks tablicy
której wartość mówi, jak długi prefiks tablicy  jest kopcowy.
jest kopcowy.