Informatyczny kącik olimpijski

Optymalna trasa łazika

Tym razem na warsztat weźmiemy zadanie Remote Rover, które pojawiło się na jednym z konkursów TopCoder w roku 2005. Naszym zadaniem jest znalezienie najszybszej trasy dla marsjańskiego łazika poruszającego się po zróżnicowanym terenie.

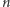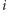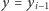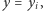Teren ten możemy przedstawić jako prostokąt, w którym początkowe położenie łazika i punkt docelowy są jego przeciwległymi wierzchołkami. Prostokąt jest podzielony na $|n$ poziomych pasów o różnej szerokości; każdy z pasów charakteryzuje się inną prędkością maksymalną, którą może osiągać na nim łazik. A konkretnie: $|i$ -ty pas jest ograniczony prostymi $|y = yi−1$ oraz $y = yi,$ a łazik może na nim jechać z prędkością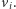 $|vi.$

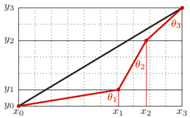
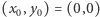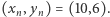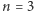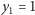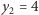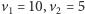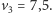Na rysunku obok przedstawiono przykładowy teren, w którym szukamy najszybszej drogi między punktami $|(x0,y0) = (0,0)$ i $(xn,yn) = (10,6).$ Podzielony jest na $n = 3$ pasy, o kolejnych szerokościach 1, 3 i 2 (wyznaczone przez proste $|y1 = 1$ i $|y2 = 4$ ) i prędkościach przejazdu $|v1 = 10, v2 = 5$ i $v3 = 7,5.$ Czas przejazdu drogą w linii prostej wynosi 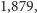$1,879,$ najkrótszy zaś czas przejazdu równy 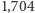$1,704$ uzyskamy, jadąc dłużej pasem dopuszczającym większą prędkość łazika, a konkretnie przejeżdżając przez zaznaczone kolorem punkty 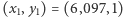$|(x1,y1) = (6,097,1)$ i $(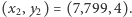x2,y2) = (7,799, 4).$

Jest jasne, że najszybsza droga między dwoma punktami na płaszczyźnie przebiega po linii prostej, ale tylko w przypadku terenu o jednakowej charakterystyce. Tak więc jeśli wyznaczymy punkty 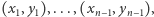$(x1,y1),...,(xn−1,yn−1),$ przez które łazik będzie przejeżdżał, zmieniając pasy, to droga będzie prowadzić odcinkami łączącymi te punkty.

Czas potrzebny na pokonanie tej drogi wyraża się wzorem

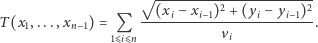√ ----------------------- (xi− xi−1)2 + (yi −yi−1)2 T(x1,...,xn−1) = Q -------------------------. 1DiDn vi

Naszym zadaniem jest znalezienie zmiennych 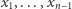$|x1,...,xn−1$ minimalizujących wartość funkcji 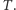$|T.$ Odpowiada to znalezieniu punktu, w którym zerują się wszystkie pochodne cząstkowe funkcji 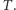$T .$ Pochodna po zmiennej 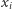$x i$ jest następująca:

$pict$

Jeśli przez 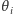$θi$ oznaczymy kąt pomiędzy linią pionową a odcinkiem łączącym punkty 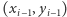$|(xi− 1,yi−1)$ i $(xi,yi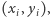),$ to dostaniemy

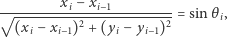--------xi-−xi−1--------- √ ---------2------------2 = sin θi, (xi− xi−1) + (yi− yi−1)

zatem pochodna po 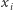$xi$ upraszcza się do

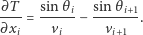∂T sin θi sinθi+1 ----= -----− -------. ∂xi vi vi+1

Jeśli więc pochodne cząstkowe względem wszystkich zmiennych 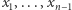$|x1,...,xn−1$ mają być równe zero, to musi być spełniony następujący układ równań:

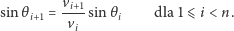v sinθi+1 =-i+1sin θi dla 1⩽ i < n. vi

(*)

Zauważmy, że ustalenie wartości 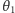$θ 1$ powoduje jednoznaczne wyznaczenie pozostałych wartości kątów, a to z kolei wyznacza nam wartości zmiennych 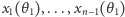$|x1(θ 1),...,xn−1(θ1)$ oraz pewną wartość zmiennej 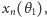$xn(θ1),$ przy czym niekoniecznie równą długości prostokąta. Innymi słowy, przy ustalonym 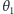$|θ1$ układ (*) określa, jakie warunki musi spełniać najszybsza droga do górnego boku prostokąta, a uzyskana wartość 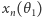$xn( θ1)$ oznacza położenie ostatniego punktu na tej drodze. 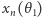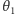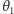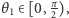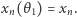Widać, że $xn(θ 1)$ jest monotoniczną funkcją zmiennej $|θ 1$ (zwiększenie $θ 1$ powoduje zwiększenie wszystkich pozostałych kątów), więc możemy zastosować wyszukiwanie binarne, aby znaleźć taką wartość $|θ1∈ [0,π 2),$ że $|xn(θ1) = xn.$ Należy jednak pamiętać o przypadku, gdy dla dużych kątów przy rozwiązywaniu układu (*) rozwiązanie nie będzie istnieć (gdy prawa strona jednego z równań będzie większa niż 1).

Na koniec wspomnijmy, że wzór (*) może być znany Czytelnikom z lekcji fizyki, gdzie pod nazwą prawa Snella opisywał zmianę kierunku biegu promienia światła przy przejściu przez granicę między dwoma ośrodkami o różnych współczynnikach załamania (zależnych od prędkości światła w tych ośrodkach). Jaki jest związek między naszym zadaniem, a zachowaniem się światła w różnych ośrodkach, pozostawiamy Czytelnikom do samodzielnego zbadania.