Informatyczny kącik olimpijski
Kolorowanie cyklu
Zagadnienie kolorowania cyklu niejednokrotnie pojawiało się na konkursach programistycznych, m.in. na Mistrzostwach Europy Środkowej w Programowaniu Zespołowym (zadanie Beijing Guards z roku 2004), czy też Mistrzostwach Polski w Programowaniu Zespołowym (zadanie Słoneczna wyspa z roku 2010).
Dany jest cykl o 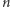 wierzchołkach
wierzchołkach 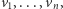 którym trzeba tak przyporządkować kolory, by:
którym trzeba tak przyporządkować kolory, by:
- (1)
- wierzchołek
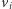 dostał dokładnie
dostał dokładnie 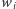 różnych kolorów;
różnych kolorów; - (2)
- każda para sąsiadujących wierzchołków dostała rozłączne zestawy kolorów;
- (3)
- liczba użytych różnych kolorów była jak najmniejsza.
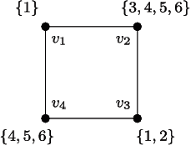
Rys. 1 Przykład dla cyklu o 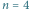 wierzchołkach i zapotrzebowaniach na kolory
wierzchołkach i zapotrzebowaniach na kolory 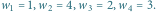 Do pokolorowania go wystarczy
Do pokolorowania go wystarczy 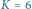 różnych kolorów.
różnych kolorów.
Zadanie to ma bardzo proste rozwiązanie w przypadku cyklu o długości parzystej. Do pokolorowania pary sąsiadujących wierzchołków 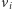 i
i 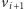 potrzebujemy
potrzebujemy 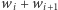 różnych kolorów (zakładamy dla uproszczenia, że
różnych kolorów (zakładamy dla uproszczenia, że 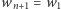 ). Zatem w sumie potrzebujemy ich co najmniej
). Zatem w sumie potrzebujemy ich co najmniej

Okazuje się, że tyle różnych kolorów wystarczy. Jeśli oznaczymy te kolory kolejnymi liczbami naturalnymi 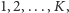 to wierzchołkom o numerach parzystych możemy przyporządkować początkowe kolory z listy, a wierzchołkom o numerach nieparzystych - kolory z końca listy. Innymi słowy, wierzchołek
to wierzchołkom o numerach parzystych możemy przyporządkować początkowe kolory z listy, a wierzchołkom o numerach nieparzystych - kolory z końca listy. Innymi słowy, wierzchołek 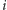 -ty dostanie kolory
-ty dostanie kolory 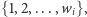 jeśli
jeśli 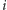 jest nieparzyste, lub kolory
jest nieparzyste, lub kolory 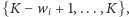 jeśli
jeśli 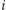 jest parzyste (patrz rysunek 1). Zauważmy, że powyższy algorytm działa nie tylko dla cyklu o długości parzystej, ale również dla ścieżek, drzew i w ogólności dla dowolnych grafów dwudzielnych.
jest parzyste (patrz rysunek 1). Zauważmy, że powyższy algorytm działa nie tylko dla cyklu o długości parzystej, ale również dla ścieżek, drzew i w ogólności dla dowolnych grafów dwudzielnych.
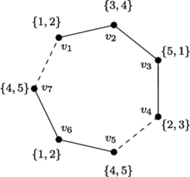
Rys. 2 Przykład dla 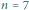 wierzchołków, z których każdy potrzebuje dwóch kolorów
wierzchołków, z których każdy potrzebuje dwóch kolorów 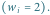 Zgodnie z algorytmem potrzebujemy
Zgodnie z algorytmem potrzebujemy 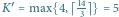 kolorów. Ponieważ
kolorów. Ponieważ 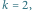 więc wierzchołki
więc wierzchołki 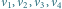 kolorujemy cyklicznie, a wierzchołki
kolorujemy cyklicznie, a wierzchołki 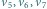 zgodnie z parzystością.
zgodnie z parzystością.
W przypadku cyklu o długości nieparzystej 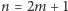 powyższe rozwiązanie nie działa. Już dla
powyższe rozwiązanie nie działa. Już dla 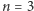 widzimy, że potrzebne jest
widzimy, że potrzebne jest 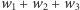 różnych kolorów. W ogólnym przypadku musimy sumarycznie wykonać
różnych kolorów. W ogólnym przypadku musimy sumarycznie wykonać 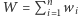 przydziałów kolorów. Ponieważ największy zbiór niezależny na cyklu (tzn. zbiór wierzchołków niepołączonych krawędziami) ma rozmiar
przydziałów kolorów. Ponieważ największy zbiór niezależny na cyklu (tzn. zbiór wierzchołków niepołączonych krawędziami) ma rozmiar 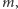 więc każdy kolor przydzielimy do co najwyżej
więc każdy kolor przydzielimy do co najwyżej 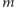 wierzchołków. Potrzebować więc będziemy co najmniej
wierzchołków. Potrzebować więc będziemy co najmniej 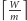 różnych kolorów. Okazuje się, że wystarczająca liczba kolorów to
różnych kolorów. Okazuje się, że wystarczająca liczba kolorów to

Niech 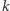 będzie taką najmniejszą liczbą, że
będzie taką najmniejszą liczbą, że 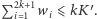 Liczba ta istnieje, bo w szczególności nierówność powyższa jest spełniona dla
Liczba ta istnieje, bo w szczególności nierówność powyższa jest spełniona dla 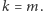 Podzielimy teraz wierzchołki cyklu na dwie grupy, które będziemy kolorować na dwa różne sposoby (patrz przykład na rysunku 2). Wierzchołki
Podzielimy teraz wierzchołki cyklu na dwie grupy, które będziemy kolorować na dwa różne sposoby (patrz przykład na rysunku 2). Wierzchołki 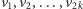 kolorujemy cyklicznie, tzn. po kolei nadając im kolory z listy
kolorujemy cyklicznie, tzn. po kolei nadając im kolory z listy

Natomiast wierzchołki 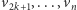 kolorujemy, używając metody dla cyklu długości parzystej, tzn. wierzchołkom nieparzystym przyporządkowujemy kolory
kolorujemy, używając metody dla cyklu długości parzystej, tzn. wierzchołkom nieparzystym przyporządkowujemy kolory 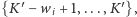 a wierzchołkom parzystym kolory
a wierzchołkom parzystym kolory 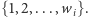
Pozostaje wykazać, że końce krawędzi łączących te dwie grupy wierzchołków są pokolorowane poprawnie. Dla krawędzi 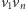 jest prosto: wierzchołek
jest prosto: wierzchołek 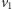 używa kolorów
używa kolorów 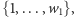 a wierzchołek
a wierzchołek 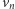 kolorów
kolorów 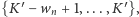 wiemy też, że
wiemy też, że 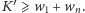 Dowód dla krawędzi
Dowód dla krawędzi 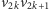 jest trudniejszy. Ponieważ
jest trudniejszy. Ponieważ

więc wierzchołkowi 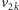 zostaną przypisane kolory ze spójnego przedziału liczb naturalnych
zostaną przypisane kolory ze spójnego przedziału liczb naturalnych 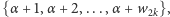 gdzie
gdzie 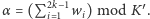 Ponadto spełnione jest
Ponadto spełnione jest 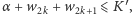 więc żaden kolor z tego przedziału nie jest kolorem ze zbioru kolorów
więc żaden kolor z tego przedziału nie jest kolorem ze zbioru kolorów 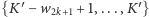 przypisanych do
przypisanych do 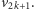
Powyższy algorytm wyznaczający kolorowanie cyklu ma złożoność czasową 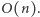
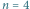 wierzchołkach i zapotrzebowaniach na kolory
wierzchołkach i zapotrzebowaniach na kolory 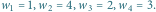 Do pokolorowania go wystarczy
Do pokolorowania go wystarczy 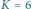 różnych kolorów.
różnych kolorów.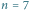 wierzchołków, z których każdy potrzebuje dwóch kolorów
wierzchołków, z których każdy potrzebuje dwóch kolorów 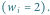 Zgodnie z algorytmem potrzebujemy
Zgodnie z algorytmem potrzebujemy 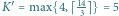 kolorów. Ponieważ
kolorów. Ponieważ 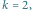 więc wierzchołki
więc wierzchołki 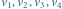 kolorujemy cyklicznie, a wierzchołki
kolorujemy cyklicznie, a wierzchołki 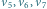 zgodnie z parzystością.
zgodnie z parzystością.