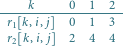Informatyczny kącik olimpijski
Wykładzina
W zeszłym miesiącu zajmowaliśmy się uogólnieniem następującego zadania: dla danego kwadratu rozmiaru 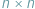 podzielonego na
podzielonego na 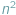 pól, z których niektóre były zabronione, należało znaleźć prostokąt o największym polu, który nie zawierał żadnego zabronionego pola. W tym numerze rozważymy jeszcze inną wariację tego zadania, a mianowicie będziemy szukać największych prostokątów, które zawierają co najwyżej
pól, z których niektóre były zabronione, należało znaleźć prostokąt o największym polu, który nie zawierał żadnego zabronionego pola. W tym numerze rozważymy jeszcze inną wariację tego zadania, a mianowicie będziemy szukać największych prostokątów, które zawierają co najwyżej 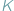 zabronionych pól (nazwiemy je prostokątami prawie pustymi).
zabronionych pól (nazwiemy je prostokątami prawie pustymi).
Na początek rozważymy przypadek 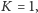 który był treścią zadania Wykładzina z finału Potyczek Algorytmicznych 2014. Zakładamy, że Czytelnicy są zaznajomieni z algorytmem szukania największego pustego prostokąta opisanym w poprzednim numerze (a pomocna może być również znajomość technik opisanych w kąciku z numeru 12/2013). Przypomnijmy, że w tamtym algorytmie ustalaliśmy wiersz
który był treścią zadania Wykładzina z finału Potyczek Algorytmicznych 2014. Zakładamy, że Czytelnicy są zaznajomieni z algorytmem szukania największego pustego prostokąta opisanym w poprzednim numerze (a pomocna może być również znajomość technik opisanych w kąciku z numeru 12/2013). Przypomnijmy, że w tamtym algorytmie ustalaliśmy wiersz 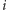 zawierający dolny bok szukanego pustego prostokąta i rozważaliśmy kolejne kolumny
zawierający dolny bok szukanego pustego prostokąta i rozważaliśmy kolejne kolumny 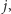 trzymając na stosie zbiór elementów opisujących obszar, w którym może znajdować się lewy górny róg pustego prostokąta o prawym dolnym rogu w polu
trzymając na stosie zbiór elementów opisujących obszar, w którym może znajdować się lewy górny róg pustego prostokąta o prawym dolnym rogu w polu 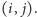

Rys. 1 Prawie pusty prostokąt dla pola  zawiera zabronione pole
zawiera zabronione pole 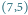 ale nie zawiera zabronionego pola
ale nie zawiera zabronionego pola 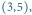 więc ma wysokość od
więc ma wysokość od 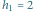 do
do 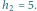 Kandydaci znajdowani przez algorytm mają rozmiary:
Kandydaci znajdowani przez algorytm mają rozmiary: 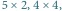
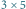 oraz
oraz 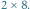
Ustalmy teraz, że szukamy prawie pustego prostokąta o dolnym boku w wierszu 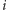 i zawierającego jedno zabronione pole w kolumnie
i zawierającego jedno zabronione pole w kolumnie 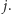 Zatem prostokąt taki będzie miał wysokość między
Zatem prostokąt taki będzie miał wysokość między ![h1 = d[i, j]+ 1](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/3x-c56f36370ed377143f8ca17e4555cd3972c9526e-im-33,33,33-FF,FF,FF.gif) a
a ![h2 = h1 +d[i − h1, j],](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/4x-c56f36370ed377143f8ca17e4555cd3972c9526e-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie ![| d[i, j]](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/5x-c56f36370ed377143f8ca17e4555cd3972c9526e-im-33,33,33-FF,FF,FF.gif) to liczba niezabronionych pól leżących na i powyżej pola
to liczba niezabronionych pól leżących na i powyżej pola 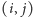 do pierwszego zabronionego pola (Rys. 1). Załóżmy też, że obliczyliśmy stos dla obszaru obejmującego kolumny
do pierwszego zabronionego pola (Rys. 1). Załóżmy też, że obliczyliśmy stos dla obszaru obejmującego kolumny 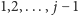 oraz symetryczny stos dla kolumn
oraz symetryczny stos dla kolumn  a także usunęliśmy z tych stosów elementy wyższe niż
a także usunęliśmy z tych stosów elementy wyższe niż  (zostawiając co najwyżej po jednym elemencie wyższym niż
(zostawiając co najwyżej po jednym elemencie wyższym niż 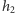 ). Wszystkich kandydatów na prawie pusty prostokąt możemy znaleźć podczas usuwania z tych stosów elementów o wysokościach pomiędzy
). Wszystkich kandydatów na prawie pusty prostokąt możemy znaleźć podczas usuwania z tych stosów elementów o wysokościach pomiędzy 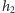 a
a 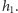
Aby uzyskać optymalną złożoność, wykonujemy jedynie dwa przebiegi oryginalnego algorytmu (jeden od lewej do prawej, a drugi od prawej do lewej), spamiętując dla każdej kolumny  listę prostokątów usuwanych ze stosu podczas przetwarzania tej kolumny. Następnie kandydatów na prawie puste prostokąty dla kolumny
listę prostokątów usuwanych ze stosu podczas przetwarzania tej kolumny. Następnie kandydatów na prawie puste prostokąty dla kolumny  uzyskujemy, przeglądając te listy. Dla ustalonego wiersza
uzyskujemy, przeglądając te listy. Dla ustalonego wiersza 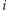 praca algorytmu jest ograniczona przez
praca algorytmu jest ograniczona przez 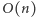 (tylko tyle elementów będzie na stosie), zatem cały algorytm działa w czasie
(tylko tyle elementów będzie na stosie), zatem cały algorytm działa w czasie 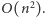
Zadanie to ma również ciekawe rozwiązanie randomizowane, w którym algorytm szukania największego pustego prostokąta wykorzystujemy bardziej bezpośrednio. Wykonujemy 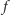 iteracji; w każdej z nich każde zabronione pole zamieniamy, niezależnie z prawdopodobieństwem
iteracji; w każdej z nich każde zabronione pole zamieniamy, niezależnie z prawdopodobieństwem  na pole niezabronione. Następnie szukamy największego pustego prostokąta. Zauważmy, że ustalony maksymalny prawie pusty prostokąt, zawiera jedno zabronione pole oraz opiera się na trzech zabronionych polach (nie na czterech, bo ustalamy również dolny bok tego prostokąta). Zatem jeśli zamienimy pole w środku oraz nie zamienimy pól na bokach (co wydarzy się z prawdopodobieństwem
na pole niezabronione. Następnie szukamy największego pustego prostokąta. Zauważmy, że ustalony maksymalny prawie pusty prostokąt, zawiera jedno zabronione pole oraz opiera się na trzech zabronionych polach (nie na czterech, bo ustalamy również dolny bok tego prostokąta). Zatem jeśli zamienimy pole w środku oraz nie zamienimy pól na bokach (co wydarzy się z prawdopodobieństwem 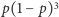 ), to ten prawie pusty prostokąt zostanie znaleziony przez algorytm szukania największego pustego prostokąta. Prawdopodobieństwo znalezienia jest największe dla
), to ten prawie pusty prostokąt zostanie znaleziony przez algorytm szukania największego pustego prostokąta. Prawdopodobieństwo znalezienia jest największe dla 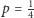 i wynosi około
i wynosi około 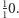 Zatem po
Zatem po 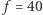 iteracjach prawdopodobieństwo znalezienia ustalonego (a zatem też tego o największym polu) prawie pustego prostokąta wynosi
iteracjach prawdopodobieństwo znalezienia ustalonego (a zatem też tego o największym polu) prawie pustego prostokąta wynosi

Zauważmy, że nasz algorytm może znajdować również prostokąty, które zawierają więcej niż jedno zabronione pole. Łatwo sobie z tym poradzimy, sprawdzając ile zabronionych pól zawiera każdy znaleziony kandydat (jak to zrobić w czasie stałym zostawimy jako nietrudne zadanie dla Czytelników, wymagające wykorzystania tzw. dwuwymiarowych sum prefiksowych). Ostateczna złożoność czasowa to 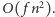 Dla pełności dodajmy, że rozwiązanie randomizowane łatwo uogólnić na przypadek
Dla pełności dodajmy, że rozwiązanie randomizowane łatwo uogólnić na przypadek 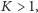 ale nie będzie to zbyt praktyczne, gdyż
ale nie będzie to zbyt praktyczne, gdyż 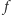 rośnie wtedy wykładniczo względem
rośnie wtedy wykładniczo względem 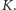

Rys. 2 Wysokości prostokątów dla 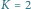 i przedziału kolumn
i przedziału kolumn 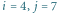 są następujące:
są następujące:

Aby rozwiązać ogólny przypadek 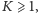 użyjemy metody "dziel i zwyciężaj". Podzielimy kwadrat poziomą prostą na dwie równe części, w których rekurencyjnie znajdziemy największe prawie puste prostokąty w całości zawarte w tych częściach. Pozostaną do rozważenia prawie puste prostokąty przecinające prostą (Rys. 2). Dla każdego
użyjemy metody "dziel i zwyciężaj". Podzielimy kwadrat poziomą prostą na dwie równe części, w których rekurencyjnie znajdziemy największe prawie puste prostokąty w całości zawarte w tych częściach. Pozostaną do rozważenia prawie puste prostokąty przecinające prostą (Rys. 2). Dla każdego  oraz dla każdej pary kolumn
oraz dla każdej pary kolumn 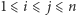 znajdźmy wysokość
znajdźmy wysokość ![r1[k,i, j]](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/4x-789515b125986a2f4c0adef7a30f8d2e6965cf33-im-33,33,33-FF,FF,FF.gif) maksymalnego prostokąta znajdującego się w górnej części, ograniczonego prostą oraz kolumnami
maksymalnego prostokąta znajdującego się w górnej części, ograniczonego prostą oraz kolumnami 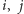 i zawierającego
i zawierającego 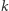 zabronionych pól - nie jest trudno zrobić to w czasie
zabronionych pól - nie jest trudno zrobić to w czasie 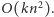 Następnie zróbmy to samo dla dolnej części, dostając wartości
Następnie zróbmy to samo dla dolnej części, dostając wartości ![r2[k,i, j].](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/8x-789515b125986a2f4c0adef7a30f8d2e6965cf33-im-33,33,33-FF,FF,FF.gif) Maksymalny prawie pusty prostokąt przecinający prostą ma rozmiar
Maksymalny prawie pusty prostokąt przecinający prostą ma rozmiar
![maxi, j( j +1 −i) ⋅(maxk1+k2DK r1[k1,i, j]+ r2[k2,i, j]).](/math/temat/informatyka/algorytmy/2015/11/29/Wykladzina/9x-789515b125986a2f4c0adef7a30f8d2e6965cf33-dm-33,33,33-FF,FF,FF.gif)
Jeśli oznaczymy przez 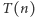 czas działania algorytmu dla kwadratu o boku
czas działania algorytmu dla kwadratu o boku 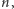 to dostajemy następującą rekurencję:
to dostajemy następującą rekurencję: 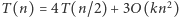 (najpierw dzielimy kwadrat na dwie prostokątne części, a potem każdą z nich pionową prostą na dwa kwadraty o bokach
(najpierw dzielimy kwadrat na dwie prostokątne części, a potem każdą z nich pionową prostą na dwa kwadraty o bokach 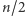 ). Rozwiązanie tej rekurencji (a zatem złożoność czasowa całego algorytmu) to
). Rozwiązanie tej rekurencji (a zatem złożoność czasowa całego algorytmu) to 
 zawiera zabronione pole
zawiera zabronione pole  ale nie zawiera zabronionego pola
ale nie zawiera zabronionego pola 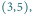 więc ma wysokość od
więc ma wysokość od  do
do 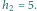 Kandydaci znajdowani przez algorytm mają rozmiary:
Kandydaci znajdowani przez algorytm mają rozmiary: 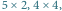
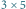 oraz
oraz 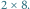
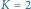 i przedziału kolumn
i przedziału kolumn 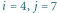 są następujące:
są następujące: