Zliczamy skojarzenia (II). O planarności i algorytmie FKT
W pierwszej części tego artykułu pokazaliśmy, że dla szczególnej klasy grafów (kraty i ich podgrafy), istnieje działający w czasie wielomianowym algorytm, który wyznacza liczbę doskonałych skojarzeń dla dowolnego grafu z tej klasy. Ten wynik można uogólnić na szerszą klasę grafów - a konkretnie na grafy planarne, czyli takie, które można narysować na płaszczyźnie tak, by żadne z ich krawędzi się nie przecinały.
Mając dowolny nieskierowany graf planarny 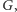 zawierający
zawierający  wierzchołków
wierzchołków 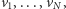 rozważymy jego (symetryczną) macierz sąsiedztwa
rozważymy jego (symetryczną) macierz sąsiedztwa 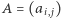 rozmiaru
rozmiaru 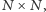 w której
w której 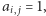 jeśli wierzchołki
jeśli wierzchołki  oraz
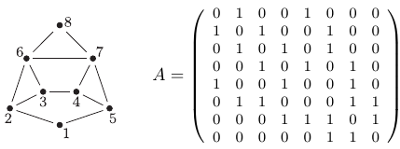
oraz  są połączone krawędzią. Przykładowo, poniższy graf o ośmiu wierzchołkach, mający cztery doskonałe skojarzenia (dwa zawierające krawędź
są połączone krawędzią. Przykładowo, poniższy graf o ośmiu wierzchołkach, mający cztery doskonałe skojarzenia (dwa zawierające krawędź  i dwa jej niezawierające), ma następującą macierz sąsiedztwa.
i dwa jej niezawierające), ma następującą macierz sąsiedztwa.
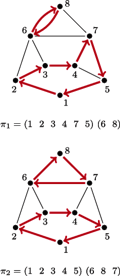
Rys. 1 Skierowane pokrycia cyklowe (wyróżnione strzałkami) w grafie 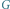 odpowiadające permutacjom
odpowiadające permutacjom 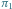 i
i 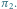
Podobnie jak w pierwszej części, naszym głównym narzędziem będzie obliczenie permanentu pewnej macierzy związanej z grafem, przy użyciu algorytmu liczenia wyznacznika jeszcze innej macierzy. Zarówno permanent, jak i wyznacznik, będą sumami iloczynów odpowiadających każdej permutacji wierzchołków grafu. Na początek zastanówmy się zatem, jakiemu obiektowi w grafie 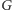 odpowiada permutacja wierzchołków
odpowiada permutacja wierzchołków  dla której iloczyn
dla której iloczyn 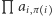 jest równy 1. Dla każdego czynnika
jest równy 1. Dla każdego czynnika 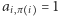 wyróżnijmy w grafie skierowaną krawędź z wierzchołka
wyróżnijmy w grafie skierowaną krawędź z wierzchołka 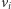 do wierzchołka
do wierzchołka 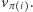 Ponieważ
Ponieważ 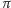 jest permutacją, więc każdy z wierzchołków będzie miał wyróżnioną dokładnie jedną krawędź wychodzącą i dokładnie jedną wchodzącą. Zatem wyróżnione krawędzie będą tworzyły skierowane pokrycie cyklowe (Rys. 1). Innymi słowy, permanent macierzy
jest permutacją, więc każdy z wierzchołków będzie miał wyróżnioną dokładnie jedną krawędź wychodzącą i dokładnie jedną wchodzącą. Zatem wyróżnione krawędzie będą tworzyły skierowane pokrycie cyklowe (Rys. 1). Innymi słowy, permanent macierzy  będzie oznaczał ich liczbę:
będzie oznaczał ich liczbę:

I w tym momencie to właśnie te pokrycia będą nas najbardziej interesowały (a dlaczego, to wyjaśni się pod koniec artykułu). W szczególności, pokażemy teraz ciekawą konstrukcję, która pozwoli nam policzyć te skierowane pokrycia cyklowe, które zawierają jedynie cykle długości parzystej.
Zamiast symetrycznej macierzy 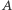 do reprezentowania grafu
do reprezentowania grafu 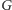 możemy równie dobrze użyć antysymetrycznej macierzy
możemy równie dobrze użyć antysymetrycznej macierzy 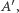 w której
w której 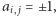 jeśli wierzchołki
jeśli wierzchołki 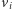 oraz
oraz  są połączone krawędzią, oraz
są połączone krawędzią, oraz 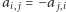 (dla ustalenia uwagi przyjmijmy, że
(dla ustalenia uwagi przyjmijmy, że 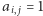 dla
dla 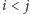 ). Innymi słowy, każdej krawędzi
). Innymi słowy, każdej krawędzi  przypisujemy etykietę 1 lub
przypisujemy etykietę 1 lub 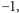 którą będziemy "odczytywać", przechodząc tą krawędzią z
którą będziemy "odczytywać", przechodząc tą krawędzią z 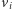 do
do 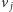 (a przechodząc ją w odwrotnym kierunku, odczytamy etykietę przeciwną). Obchodząc dowolny cykl w grafie
(a przechodząc ją w odwrotnym kierunku, odczytamy etykietę przeciwną). Obchodząc dowolny cykl w grafie 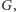 będziemy mnożyć etykiety jego krawędzi, uzyskując wkład, jaki daje ten cykl do iloczynu
będziemy mnożyć etykiety jego krawędzi, uzyskując wkład, jaki daje ten cykl do iloczynu  Oczywiście, jeśli przejdziemy taki cykl w odwrotnym kierunku, to jego wkład przemnoży się przez
Oczywiście, jeśli przejdziemy taki cykl w odwrotnym kierunku, to jego wkład przemnoży się przez 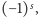 gdzie
gdzie  jest długością cyklu, w szczególności zmieni znak dla cyklu nieparzystej długości. Dla skierowanego pokrycia cyklowego odpowiadającego permutacji
jest długością cyklu, w szczególności zmieni znak dla cyklu nieparzystej długości. Dla skierowanego pokrycia cyklowego odpowiadającego permutacji 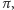 przez wkład pokrycia rozumiemy iloczyn wkładów wszystkich cykli, czyli po prostu
przez wkład pokrycia rozumiemy iloczyn wkładów wszystkich cykli, czyli po prostu 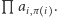
Pokażemy teraz, że można połączyć skierowane pokrycia cyklowe, które zawierają jakikolwiek cykl nieparzysty, w takie pary, że wkłady pokryć należących do każdej pary będą miały różne znaki. W tym celu ustawmy wszystkie skierowane cykle długości nieparzystej z grafu 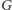 w ciąg
w ciąg 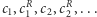 (gdzie
(gdzie 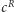 oznacza ten sam cykl co
oznacza ten sam cykl co  tylko przeciwnie skierowany). Jeśli w pokryciu cyklowym
tylko przeciwnie skierowany). Jeśli w pokryciu cyklowym  jest najmniejszym cyklem z ciągu, to sparujemy je z pokryciem cyklowym, w którym ten cykl zamienimy na
jest najmniejszym cyklem z ciągu, to sparujemy je z pokryciem cyklowym, w którym ten cykl zamienimy na  Zauważmy, że parowanie jest poprawne oraz iloczyny
Zauważmy, że parowanie jest poprawne oraz iloczyny 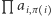 dla pokryć z każdej pary mają przeciwne znaki. Z tego wynika, że jeśli przesumujemy teraz te iloczyny dla wszystkich skierowanych pokryć cyklowych, które zawierają jakikolwiek cykl nieparzysty, to suma ta wyniesie 0. Tak więc w przypadku macierzy antysymetrycznej
dla pokryć z każdej pary mają przeciwne znaki. Z tego wynika, że jeśli przesumujemy teraz te iloczyny dla wszystkich skierowanych pokryć cyklowych, które zawierają jakikolwiek cykl nieparzysty, to suma ta wyniesie 0. Tak więc w przypadku macierzy antysymetrycznej 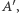 zarówno wartości
zarówno wartości 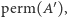 jak i
jak i 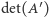 nie zmienią się, jeśli w sumowaniu opuścimy wszystkie permutacje zawierające jakikolwiek cykl nieparzysty.
nie zmienią się, jeśli w sumowaniu opuścimy wszystkie permutacje zawierające jakikolwiek cykl nieparzysty.
Z cyklami parzystymi jest kłopot - choć wkład z odwróconego cyklu jest taki sam, jak dla oryginalnego, to istotnie zależy on od konkretnych etykiet. Dla skierowanego cyklu  oznaczmy przez
oznaczmy przez 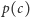 parzystość liczby krawędzi, dla których odczytujemy etykietę
parzystość liczby krawędzi, dla których odczytujemy etykietę  (zatem wkład z tego cyklu jest równy 1, jeśli
(zatem wkład z tego cyklu jest równy 1, jeśli  jest parzyste i
jest parzyste i 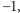 jeśli jest nieparzyste). Okazuje się, że w przypadku grafów planarnych jesteśmy w stanie w sposób wystarczający kontrolować liczbę
jeśli jest nieparzyste). Okazuje się, że w przypadku grafów planarnych jesteśmy w stanie w sposób wystarczający kontrolować liczbę 
Rys. 2 Wierzchołki grafu dualnego grafu 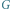 oraz krawędzie jego drzewa rozpinającego
oraz krawędzie jego drzewa rozpinającego 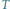 (wyróżnione kolorem) oraz krawędzie tnące grafu
(wyróżnione kolorem) oraz krawędzie tnące grafu 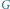 (pogrubione).
(pogrubione).
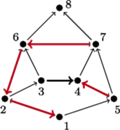
Rys. 3 Aby każdy cykl ściany dostał parzystość 1, algorytm FKT zmienił skierowanie czterech spośród pięciu krawędzi tnących. Dzięki temu każdy cykl należący do skierowanego pokrycia parzystego ma parzystość 1. Ale nie każdy cykl parzysty ma tę własność, patrz np. cykl (1, 2, 3, 6, 7, 5).
Graf planarny 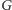 możemy narysować na płaszczyźnie tak, że żadne krawędzie nie będą się przecinały. Każda część płaszczyzny otoczona krawędziami to ściana grafu
możemy narysować na płaszczyźnie tak, że żadne krawędzie nie będą się przecinały. Każda część płaszczyzny otoczona krawędziami to ściana grafu  Z grafem tym możemy związać graf dualny, w którym mamy wierzchołek dla każdej ściany grafu
Z grafem tym możemy związać graf dualny, w którym mamy wierzchołek dla każdej ściany grafu  oraz krawędź, jeśli dwie ściany mają wspólną krawędź w
oraz krawędź, jeśli dwie ściany mają wspólną krawędź w  W grafie dualnym wyróżnimy też dowolne ukorzenione drzewo rozpinające
W grafie dualnym wyróżnimy też dowolne ukorzenione drzewo rozpinające  (Rys. 2), a w grafie
(Rys. 2), a w grafie  zbiór krawędzi, które przecinają
zbiór krawędzi, które przecinają  (nazwiemy je krawędziami tnącymi). Będziemy teraz zmieniać etykietowanie niektórych z krawędzi tnących. Zauważmy, że dowolna ściana grafu
(nazwiemy je krawędziami tnącymi). Będziemy teraz zmieniać etykietowanie niektórych z krawędzi tnących. Zauważmy, że dowolna ściana grafu 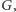 odpowiadająca pewnemu liściowi
odpowiadająca pewnemu liściowi  drzewa
drzewa 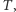 ma dokładnie jedną krawędź tnącą. Zmieniając (albo nie) etykietowanie tej krawędzi, możemy wymusić dowolną parzystość wartości
ma dokładnie jedną krawędź tnącą. Zmieniając (albo nie) etykietowanie tej krawędzi, możemy wymusić dowolną parzystość wartości 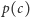 dla cyklu
dla cyklu  otaczającego tę ścianę. Następnie usuwamy liść
otaczającego tę ścianę. Następnie usuwamy liść  z drzewa
z drzewa 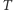 i postępujemy rekurencyjnie, aż rozważymy wszystkie ściany. Powyższy algorytm (znany pod nazwą FKT od nazwisk jego twórców - Fisher, Kasteleyn i Temperley), pozwala nam wymusić dowolną parzystość
i postępujemy rekurencyjnie, aż rozważymy wszystkie ściany. Powyższy algorytm (znany pod nazwą FKT od nazwisk jego twórców - Fisher, Kasteleyn i Temperley), pozwala nam wymusić dowolną parzystość 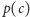 krawędzi dla każdego cyklu
krawędzi dla każdego cyklu  odpowiadającego ścianie grafu (Rys. 3).
odpowiadającego ścianie grafu (Rys. 3).
A jak to wpływa na parzystości pozostałych cykli? Łatwo wykazać, że jeśli mamy cykle  i
i 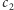 odpowiadające sąsiadującym ścianom grafu, to parzystość cyklu, który otacza obie te ściany, wynosi
odpowiadające sąsiadującym ścianom grafu, to parzystość cyklu, który otacza obie te ściany, wynosi 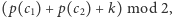 gdzie
gdzie 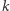 jest liczbą krawędzi wspólnych dla obu tych ścian. Indukcyjnie można zatem wykazać, że cykl
jest liczbą krawędzi wspólnych dla obu tych ścian. Indukcyjnie można zatem wykazać, że cykl  otaczający ściany cyklów
otaczający ściany cyklów 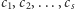 ma parzystość
ma parzystość  gdzie
gdzie 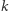 to liczba krawędzi leżących "wewnątrz" cyklu
to liczba krawędzi leżących "wewnątrz" cyklu 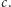 Wzór ten ma ciekawe konsekwencje, jeśli ustalimy parzystość każdej ze ścian na
Wzór ten ma ciekawe konsekwencje, jeśli ustalimy parzystość każdej ze ścian na 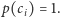 Wtedy parzystość cyklu
Wtedy parzystość cyklu  to
to 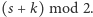 Ale, używając wzoru Eulera, można wykazać, że liczba wierzchołków leżących "wewnątrz" cyklu
Ale, używając wzoru Eulera, można wykazać, że liczba wierzchołków leżących "wewnątrz" cyklu  to
to  W szczególności
W szczególności  wtedy, gdy liczba tych wierzchołków jest parzysta.
wtedy, gdy liczba tych wierzchołków jest parzysta.
Cała ta karkołomna konstrukcja znajdzie zaraz swoje uzasadnienie. Zacznijmy od macierzy 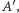 a następnie wykonajmy algorytm FKT tak, by parzystość cyklu każdej ściany wyniosła 1. Zdefiniujmy już ostatnią macierz antysymetryczną
a następnie wykonajmy algorytm FKT tak, by parzystość cyklu każdej ściany wyniosła 1. Zdefiniujmy już ostatnią macierz antysymetryczną 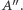 Dla
Dla 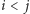 i wierzchołków
i wierzchołków 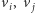 połączonych krawędzią kładziemy
połączonych krawędzią kładziemy 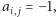 jeśli etykietowanie krawędzi zostało zmienione przez algorytm FKT, oraz
jeśli etykietowanie krawędzi zostało zmienione przez algorytm FKT, oraz 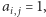 jeśli nie zostało (oczywiście
jeśli nie zostało (oczywiście 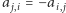 ). Rozważmy teraz dowolny cykl
). Rozważmy teraz dowolny cykl  należący do pewnego pokrycia cyklowego cyklami parzystymi. Wszystkie wierzchołki leżące wewnątrz tego cyklu muszą być również pokryte pełnymi cyklami, zatem ich liczba musi być parzysta, więc
należący do pewnego pokrycia cyklowego cyklami parzystymi. Wszystkie wierzchołki leżące wewnątrz tego cyklu muszą być również pokryte pełnymi cyklami, zatem ich liczba musi być parzysta, więc  Innymi słowy, iloczyn etykiet krawędzi z tego cyklu wynosi
Innymi słowy, iloczyn etykiet krawędzi z tego cyklu wynosi  niezależnie od wyboru tego cyklu. Tak więc znowu (tak jak w pierwszej części artykułu) udało nam się sprawić, że iloczyn
niezależnie od wyboru tego cyklu. Tak więc znowu (tak jak w pierwszej części artykułu) udało nam się sprawić, że iloczyn 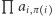 wszystkich cykli jest równy znakowi permutacji, więc możemy użyć algorytmu liczenia wyznacznika. Zatem
wszystkich cykli jest równy znakowi permutacji, więc możemy użyć algorytmu liczenia wyznacznika. Zatem


Rys. 4 Para skojarzeń, która odpowiada pierwszemu pokryciu cyklowemu z rysunku 1.
Pora na ostatnią sztuczkę. Rozważmy parę doskonałych skojarzeń w grafie i zaznaczmy naraz ich krawędzie. Ponieważ każdy wierzchołek będzie miał zaznaczone dokładnie dwie krawędzie, więc taki rysunek odpowiadać będzie pewnemu pokryciu cyklowemu cyklami parzystymi. Co więcej, każdy cykl długości większej niż 2 możemy skierować - powiedzmy, że kierujemy go w prawo dokładnie wtedy, gdy najmniejsza leksykograficznie krawędź pochodzi z pierwszego skojarzenia (Rys. 4). Nietrudno się przekonać, że w ten sposób dostaniemy bijekcję między zbiorem uporządkowanych par doskonałych skojarzeń a zbiorem skierowanych pokryć cyklowych cyklami parzystymi (aby uzyskać z pokrycia parę skojarzeń, należy brać co drugą krawędź z każdego cyklu). Porównując liczności tych zbiorów, dostajemy ostateczny wzór na liczbę doskonałych skojarzeń w grafie planarnym:

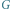 odpowiadające permutacjom
odpowiadające permutacjom 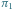 i
i 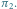
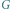 oraz krawędzie jego drzewa rozpinającego
oraz krawędzie jego drzewa rozpinającego 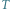 (wyróżnione kolorem) oraz krawędzie tnące grafu
(wyróżnione kolorem) oraz krawędzie tnące grafu 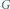 (pogrubione).
(pogrubione).