Mała Delta
Architekci i algorytmy (2)

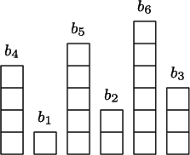
Rys. 1 Uporządkowanie generowane przez algorytm dla  budynków o wysokościach
budynków o wysokościach 
W marcowym numerze Delty postawiliśmy następujące pytanie:
Problem. w jaki sposób uszeregować 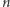 budynków o wysokościach danych ciągiem
budynków o wysokościach danych ciągiem 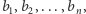 aby suma różnic wysokości sąsiadujących ze sobą budynków
aby suma różnic wysokości sąsiadujących ze sobą budynków 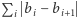 była jak największa.
była jak największa.
Przyjmijmy dla uproszczenia, że liczba budynków 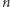 jest parzysta i równa co najmniej 4. Algorytm znajdujący optymalne uszeregowanie można opisać tak:
jest parzysta i równa co najmniej 4. Algorytm znajdujący optymalne uszeregowanie można opisać tak:
Krok 0. Uporządkuj budynki od najniższego do najwyższego. Wysokości budynków utworzą niemalejący ciąg 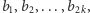 gdzie
gdzie 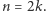
Krok 1. "Przełam" ciąg 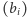 między wyrazami
między wyrazami 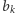 i
i 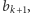 otrzymując dwa podciągi:
otrzymując dwa podciągi: 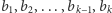 oraz
oraz 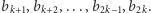
Krok 2. "Przełóż" wyrazy podciągów naprzemiennie, tak że otrzymasz ciąg

Krok 3. Ustaw w dowolnej kolejności wyrazy stojące na miejscach nieparzystych (z wyjątkiem pierwszego), tj. wyrazy 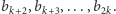
Krok 4. Ustaw w dowolnej kolejności wyrazy stojące na miejscach parzystych (z wyjątkiem ostatniego), tj. wyrazy 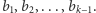
Wynik działania algorytmu dla przykładowego ciągu zilustrowano na rysunku 1. Dodajmy pewne uwagi.
Po pierwsze: instrukcja "ustaw w dowolnej kolejności" oznacza, że w wyniku wykonania algorytmu możemy uzyskać 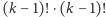 optymalnych uszeregowań. Oczywiście wygenerowane uszeregowania będą wszystkie różne tylko wówczas, gdy wszystkie wyrazy podciągów, o których mowa w krokach 3-4 algorytmu, są różne.
optymalnych uszeregowań. Oczywiście wygenerowane uszeregowania będą wszystkie różne tylko wówczas, gdy wszystkie wyrazy podciągów, o których mowa w krokach 3-4 algorytmu, są różne.
Po drugie: rozwiązań jest tak naprawdę dwa razy więcej (chyba że wszystkie wysokości budynków są jednakowe), gdyż po zapisaniu wyrazów ciągu, wygenerowanego przez algorytm, w odwrotnej kolejności, również otrzymamy optymalne uszeregowanie.
W efekcie zastosowania kroków  dla ciągu 5, 10, 10, 15, 25, 25, 30 i 45 otrzymamy optymalny ciąg 25, 5, 25, 10, 30, 10, 45, 15. Wszystkich optymalnych rozwiązań, które uzyskujemy wykonując kroki
dla ciągu 5, 10, 10, 15, 25, 25, 30 i 45 otrzymamy optymalny ciąg 25, 5, 25, 10, 30, 10, 45, 15. Wszystkich optymalnych rozwiązań, które uzyskujemy wykonując kroki 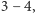 jest w sumie 36 (dlaczego?).
jest w sumie 36 (dlaczego?).
Jak uzasadnić, że przedstawiony wyżej algorytm daje optymalne rozwiązanie, czyli takie uszeregowanie budynków, że suma różnic wysokości sąsiednich budynków będzie największa z możliwych?
Zauważmy, że jeśli dwa budynki 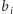 i
i 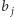 sąsiadują (przy czym
sąsiadują (przy czym 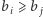 ), to ich wkład w sumę różnic wynosi
), to ich wkład w sumę różnic wynosi 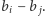 Zatem dla każdej pary wkład to różnica wysokości wyższego budynku i wysokości niższego budynku. Mamy
Zatem dla każdej pary wkład to różnica wysokości wyższego budynku i wysokości niższego budynku. Mamy 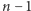 takich par, a każdy budynek (oprócz skrajnych) należy do dwóch takich par. Zatem sumę różnic można zapisać jako
takich par, a każdy budynek (oprócz skrajnych) należy do dwóch takich par. Zatem sumę różnic można zapisać jako

gdzie wśród wartości 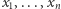 oraz
oraz 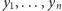 dokładnie dwie są równe 0, dokładnie
dokładnie dwie są równe 0, dokładnie 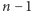 wartości jest równych 1 i dokładnie
wartości jest równych 1 i dokładnie 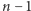 wartości jest równych
wartości jest równych 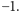 Można zauważyć, że dla
Można zauważyć, że dla 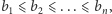 suma
suma 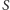 przyjmie maksymalną wartość wtedy, gdy
przyjmie maksymalną wartość wtedy, gdy 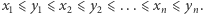
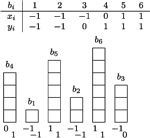
Rys. 2 Pod budynkiem 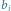 zapisano odpowiadające mu wartości
zapisano odpowiadające mu wartości 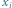 i
i 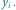
Pozostaje wykazać, że istnieje uszeregowanie, które realizuje tę sumę. Łatwo się przekonać, że jest to, na przykład, uporządkowanie uzyskane w kroku 2 algorytmu. Wówczas wartości 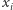 i
i 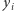 dla
dla 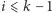 są równe
są równe 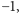 wartość
wartość 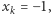 wartości
wartości 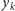 i
i 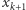 są równe 0, wartość
są równe 0, wartość 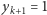 oraz wartości
oraz wartości 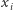 i
i 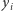 dla
dla 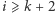 są równe 1 (Rys. 2). Tak więc
są równe 1 (Rys. 2). Tak więc

Zauważmy również, że permutacje, które wykonujemy w krokach  algorytmu, nie zmieniają wartości
algorytmu, nie zmieniają wartości 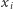 i
i 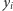 dla indeksów
dla indeksów 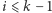 oraz
oraz 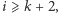 zatem nie psują optymalności rozwiązania.
zatem nie psują optymalności rozwiązania.
Jako zadanie dla Czytelników pozostawiamy uzasadnienie, że algorytm generuje wszystkie możliwe optymalne uszeregowania budynków, czyli że wyrazy podciągów, o których mowa w kroku 1, muszą występować naprzemiennie. (Można tu skorzystać z obserwacji, że permutacje z kroków  są jedynymi, które nie zmieniają wartości
są jedynymi, które nie zmieniają wartości 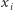 i
i  i popatrzeć, co się dzieje z sumą
i popatrzeć, co się dzieje z sumą  jeśli któreś z wartości zostaną zmienione.)
jeśli któreś z wartości zostaną zmienione.)
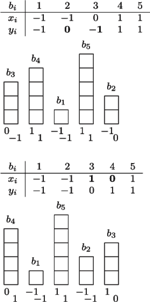
Rys. 3 Przykładowe porządkowania dla nieparzystej liczby budynków.
Czytelnik Wnikliwy może zapytać: a co w przypadku, gdy  jest liczbą nieparzystą? Czy przedstawiony wyżej algorytm można w prosty sposób zaadaptować dla takiej sytuacji? Okazuje się, że tak! W jaki sposób to zrobić?
jest liczbą nieparzystą? Czy przedstawiony wyżej algorytm można w prosty sposób zaadaptować dla takiej sytuacji? Okazuje się, że tak! W jaki sposób to zrobić?
Gdy 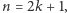 dla pewnego naturalnego
dla pewnego naturalnego 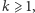 mamy
mamy 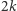 par sąsiadujących budynków, a każdy budynek (oprócz skrajnych) należy do dwóch takich par. Postępując jak poprzednio, sumę różnic można zapisać jako
par sąsiadujących budynków, a każdy budynek (oprócz skrajnych) należy do dwóch takich par. Postępując jak poprzednio, sumę różnic można zapisać jako

gdzie wśród wartości 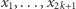 oraz
oraz 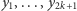 dwie są równe 0,
dwie są równe 0, 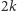 wartości jest równych 1, a
wartości jest równych 1, a 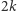 wartości jest równych
wartości jest równych 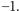 Znowu dla niemalejącego ciągu
Znowu dla niemalejącego ciągu 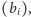 suma
suma  przyjmie maksymalną wartość wtedy, gdy
przyjmie maksymalną wartość wtedy, gdy 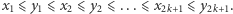 Można się jednak przekonać, że dla żadnego
Można się jednak przekonać, że dla żadnego 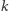 nie istnieje takie uszeregowanie, że wartości
nie istnieje takie uszeregowanie, że wartości 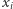 i
i 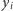 dla
dla 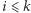 są równe
są równe 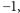 wartości
wartości 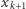 i
i 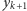 są równe 0, a wartości
są równe 0, a wartości 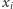 i
i 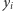 dla
dla 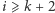 są równe 1, gdyż wartości 0 muszą być przypisane skrajnym, a więc różnym, budynkom (inaczej oznaczałoby to, że budynek o wysokości
są równe 1, gdyż wartości 0 muszą być przypisane skrajnym, a więc różnym, budynkom (inaczej oznaczałoby to, że budynek o wysokości 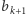 jest skrajnym zarówno z lewej, jak i prawej strony). Kiedy zatem suma
jest skrajnym zarówno z lewej, jak i prawej strony). Kiedy zatem suma  będzie największa? Są trzy możliwości.
będzie największa? Są trzy możliwości.
- (1)
- Jeśli
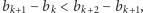 to maksymalna suma będzie odpowiadać zamianie wartości
to maksymalna suma będzie odpowiadać zamianie wartości 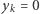 i
i 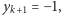 a więc np. uszeregowaniu
a więc np. uszeregowaniu 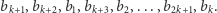
- (2)
- Jeśli
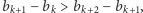 to maksymalna suma będzie odpowiadać zamianie wartości
to maksymalna suma będzie odpowiadać zamianie wartości 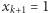 i
i 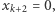 a więc np. uszeregowaniu
a więc np. uszeregowaniu 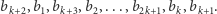
- (3)
- Jeśli
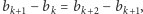 to oba wyżej wymienione uszeregowania będą związane z maksymalną sumą (Rys. 3).
to oba wyżej wymienione uszeregowania będą związane z maksymalną sumą (Rys. 3).
Przeprowadzając analogiczne rozumowanie jak w przypadku  parzystego, można pokazać, że wykonując pewne permutacje, możemy otrzymać więcej optymalnych uszeregowań budynków. Gdy wszystkie wysokości budynków są różne, to ich liczba jest równa
parzystego, można pokazać, że wykonując pewne permutacje, możemy otrzymać więcej optymalnych uszeregowań budynków. Gdy wszystkie wysokości budynków są różne, to ich liczba jest równa 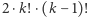 (lub jeszcze dwa razy większa, jeśli mamy do czynienia z trzecią możliwością z powyższej listy).
(lub jeszcze dwa razy większa, jeśli mamy do czynienia z trzecią możliwością z powyższej listy).
Przy okazji: "przełamywanie" ciągu i naprzemienne "przekładanie" wyrazów podciągów może Czytelnikowi przypominać tasowanie kart w grach karcianych. To celne spostrzeżenie! Więcej na temat teorii tasowania kart (i nie tylko) Czytelnik znajdzie w książce Iana Stewarta pt. Jak pokroić tort i inne zagadki matematyczne, wydanej w języku polskim w 2012 roku.
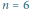 budynków o wysokościach
budynków o wysokościach 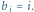
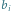 zapisano odpowiadające mu wartości
zapisano odpowiadające mu wartości 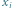 i
i