Grupowa eksploracja
Wyobraźmy sobie sytuację, w której grupa speleologów chce wyeksplorować nieznaną jaskinię. Przy każdym rozgałęzieniu muszą podejmować decyzję, ilu z nich pójdzie każdym z nowych tuneli.
Być może czasami będzie się opłacało zostawić część z nich przy rozgałęzieniu. Niektóre z tuneli będą się, być może, kończyły ślepo, a niektóre będą się dalej rozgałęziały. Speleolodzy mają telefony i mogą się ze sobą komunikować, więc gdy jeden z nich odkryje tunel z dużą liczbą rozgałęzień, może wezwać posiłki. Intuicyjnie rozsądne wydaje się wysyłanie większej liczby speleologów w te rejony jaskini, w których jest więcej tuneli. Chcielibyśmy jakoś sformalizować (i nieco uprościć) ten problem i przeanalizować takie naturalne podejście. Uproszczenia będą dwa: jaskinia będzie przedstawiona jako drzewo, czyli spójny graf bez cykli, a zespół speleologów będzie dość liczny...
Problem definiujemy następująco: mamy danych 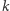 agentów, początkowo umieszczonych w korzeniu
agentów, początkowo umieszczonych w korzeniu  nieznanego drzewa
nieznanego drzewa

o znanej liczbie wierzchołków

Drzewo jest nieznane, to znaczy, że nasza początkowa wiedza to tylko liczba krawędzi wychodzących z korzenia. W pierwszym kroku nasz algorytm musi wybrać, ilu agentów przetrawersuje krawędzie wychodzące z 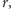 a ilu zostanie w
a ilu zostanie w  do następnej rundy. Jeżeli agentowi przydzielimy trawersowanie krawędzi z
do następnej rundy. Jeżeli agentowi przydzielimy trawersowanie krawędzi z  do pewnego sąsiada
do pewnego sąsiada 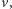 to przejście krawędzi zajmie agentowi całą rundę i pojawi się on w wierzchołku
to przejście krawędzi zajmie agentowi całą rundę i pojawi się on w wierzchołku  na początku następnej rundy. W następnej rundzie będzie on mógł przetrawersować dowolną krawędź wychodzącą z
na początku następnej rundy. W następnej rundzie będzie on mógł przetrawersować dowolną krawędź wychodzącą z 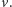 Wszyscy agenci, którzy w danej rundzie przechodzą krawędzie, robią to równocześnie.
Wszyscy agenci, którzy w danej rundzie przechodzą krawędzie, robią to równocześnie.
Przez 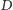 będziemy oznaczać odległość od korzenia
będziemy oznaczać odległość od korzenia  do najdalszego liścia
do najdalszego liścia 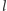 w drzewie
w drzewie 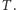 Odległość jest liczona jako liczba krawędzi na ścieżce łączącej
Odległość jest liczona jako liczba krawędzi na ścieżce łączącej  z
z 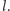 Oczywiście, nie jesteśmy w stanie wyeksplorować w czasie mniejszym niż
Oczywiście, nie jesteśmy w stanie wyeksplorować w czasie mniejszym niż 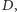 ponieważ przejście ścieżki z
ponieważ przejście ścieżki z  do
do 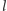 zajmuje
zajmuje 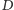 rund.
rund.
Gdy wierzchołek jest odwiedzony przez pewnego agenta po raz pierwszy, to otrzymujemy informację o jego stopniu (liczbie wychodzących krawędzi). Ponadto dostajemy też informację o tym, która krawędź prowadzi do korzenia. Po pewnej liczbie kroków eksploracji już coś wiemy o wyglądzie drzewa 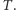 Oznaczmy przez
Oznaczmy przez 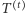 poddrzewo drzewa
poddrzewo drzewa 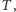 składające się z wierzchołków, które zostały poznane do chwili
składające się z wierzchołków, które zostały poznane do chwili 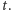 Na przykład
Na przykład 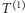 to korzeń razem z dziećmi korzenia, ponieważ już na początku pierwszej rundy wiemy, ile dzieci ma korzeń. Drzewo
to korzeń razem z dziećmi korzenia, ponieważ już na początku pierwszej rundy wiemy, ile dzieci ma korzeń. Drzewo 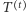 zatem zawiera pewne wierzchołki, które nie są jeszcze odwiedzone, ale są już znane. Dla
zatem zawiera pewne wierzchołki, które nie są jeszcze odwiedzone, ale są już znane. Dla 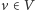 oznaczmy przez
oznaczmy przez 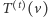 poddrzewo drzewa
poddrzewo drzewa 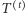 zawierające tylko te wierzchołki, dla których
zawierające tylko te wierzchołki, dla których  jest przodkiem (ucinamy krawędź łączącą
jest przodkiem (ucinamy krawędź łączącą  z jego rodzicem i dostajemy
z jego rodzicem i dostajemy 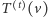 ). Przez
). Przez 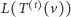 oznaczamy liczbę wierzchołków znanych, ale nieodwiedzonych w drzewie
oznaczamy liczbę wierzchołków znanych, ale nieodwiedzonych w drzewie 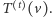 Czasami na wierzchołki znane, ale nieodwiedzone będziemy mówili "nieukończone ścieżki", ponieważ każdy taki wierzchołek jest korzeniem, być może dużego, nieznanego drzewa.
Czasami na wierzchołki znane, ale nieodwiedzone będziemy mówili "nieukończone ścieżki", ponieważ każdy taki wierzchołek jest korzeniem, być może dużego, nieznanego drzewa.
Dostajemy do dyspozycji pokaźnych rozmiarów zespół agentów

dla pewnej stałej 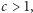 ale chcemy eksplorować szybko, czyli w czasie jak najbliższym
ale chcemy eksplorować szybko, czyli w czasie jak najbliższym 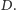
Propozycja algorytmu
Na początku wszyscy agenci w korzeniu są nieaktywni. W każdej rundzie aktywujemy  agentów w korzeniu (
agentów w korzeniu ( 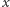 wyznaczymy później). Wszyscy aktywni agenci w każdej rundzie idą w dół drzewa. Agentów dzielimy proporcjonalnie do liczby nieukończonych ścieżek w poddrzewach. Drobnym niuansem są zaokrąglenia; w pseudokodzie zapiszemy wszystko dokładnie:
wyznaczymy później). Wszyscy aktywni agenci w każdej rundzie idą w dół drzewa. Agentów dzielimy proporcjonalnie do liczby nieukończonych ścieżek w poddrzewach. Drobnym niuansem są zaokrąglenia; w pseudokodzie zapiszemy wszystko dokładnie:

Analiza
Algorytm 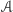 nie robi niczego odkrywczego, po prostu wysyła więcej agentów tam, gdzie jest więcej ścieżek do odkrycia. Ale jego analiza nie jest oczywista. Algorytm, odkrywając kolejne wierzchołki drzewa, na bieżąco zmienia wartości liczby nieukończonych ścieżek w poddrzewach (funkcja
nie robi niczego odkrywczego, po prostu wysyła więcej agentów tam, gdzie jest więcej ścieżek do odkrycia. Ale jego analiza nie jest oczywista. Algorytm, odkrywając kolejne wierzchołki drzewa, na bieżąco zmienia wartości liczby nieukończonych ścieżek w poddrzewach (funkcja 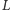 ), co ma wpływ na proporcje podziału liczby agentów. Wydaje się, że jest to kluczowa własność algorytmu, więc w naszej analizie musimy ją zbadać. Oczywiście, musimy też wyznaczyć odpowiednią wartość parametru
), co ma wpływ na proporcje podziału liczby agentów. Wydaje się, że jest to kluczowa własność algorytmu, więc w naszej analizie musimy ją zbadać. Oczywiście, musimy też wyznaczyć odpowiednią wartość parametru 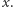 Na razie ustalmy tylko, że
Na razie ustalmy tylko, że 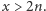
Weźmy dowolny liść 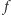 z drzewa
z drzewa 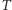 i ścieżkę długości
i ścieżkę długości 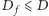 łączącą
łączącą 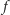 z korzeniem
z korzeniem 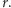 Oznaczmy tę ścieżkę przez
Oznaczmy tę ścieżkę przez 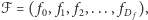 gdzie
gdzie 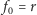 i
i 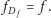 Chcemy się przyjrzeć, jak liczne grupy agentów będą wędrowały po ścieżce
Chcemy się przyjrzeć, jak liczne grupy agentów będą wędrowały po ścieżce 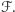 Liczba agentów wysyłana wzdłuż ścieżki zależy od liczby nieukończonych ścieżek w odpowiednich poddrzewach. Jeżeli oznaczymy
Liczba agentów wysyłana wzdłuż ścieżki zależy od liczby nieukończonych ścieżek w odpowiednich poddrzewach. Jeżeli oznaczymy 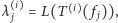 to
to 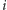 -tym w kroku z wierzchołka
-tym w kroku z wierzchołka 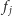 wyślemy do
wyślemy do 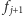 mniej więcej (z dokładnością do zaokrągleń)
mniej więcej (z dokładnością do zaokrągleń) 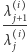 -tą część agentów znajdujących się w
-tą część agentów znajdujących się w 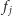 na początku rundy
na początku rundy 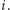 Zapomnijmy na chwilę o zaokrągleniach i pójdźmy dalej tym tropem. Do liścia
Zapomnijmy na chwilę o zaokrągleniach i pójdźmy dalej tym tropem. Do liścia 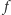 dotrze
dotrze

agentów wysłanych w rundzie 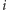 z korzenia. Zauważmy, jak wyglądają pierwsze dwie wartości:
z korzenia. Zauważmy, jak wyglądają pierwsze dwie wartości:

Jeżeli wymnożymy 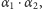 to dość dużo się uprości. Wymnóżmy zatem
to dość dużo się uprości. Wymnóżmy zatem 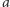 kolejnych wartości
kolejnych wartości 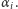 Biorąc pod uwagę, że z definicji funkcji
Biorąc pod uwagę, że z definicji funkcji 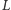 mamy
mamy 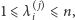 to dostaniemy
to dostaniemy 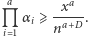 Czyli jeżeli ustalimy
Czyli jeżeli ustalimy 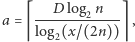 to dostaniemy
to dostaniemy 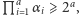 czyli dla pewnego
czyli dla pewnego 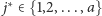 mamy
mamy 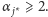 Gdyby nie było zaokrągleń i każde dziecko dostawałoby należny przydział agentów, to
Gdyby nie było zaokrągleń i każde dziecko dostawałoby należny przydział agentów, to 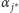 agentów spośród grupy, która wyrusza w rundzie
agentów spośród grupy, która wyrusza w rundzie 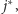 dotarłoby do liścia
dotarłoby do liścia 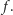 W rzeczywistości liczby agentów są czasem zaokrąglane w dół, zgodnie z regułą (i) z algorytmu, ale można pokazać, że te zaokrąglenia zbyt dużo nie psują.
W rzeczywistości liczby agentów są czasem zaokrąglane w dół, zgodnie z regułą (i) z algorytmu, ale można pokazać, że te zaokrąglenia zbyt dużo nie psują.
Przyjrzyjmy się liczbie agentów, podążających ścieżką 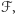 spośród grupy, która wyrusza w rundzie
spośród grupy, która wyrusza w rundzie 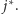 Zauważmy, że w przypadku, gdy
Zauważmy, że w przypadku, gdy 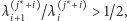 to wtedy drzewo
to wtedy drzewo 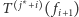 zawiera co najmniej połowę wszystkich otwartych ścieżek drzewa
zawiera co najmniej połowę wszystkich otwartych ścieżek drzewa 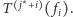 W takim przypadku wierzchołek
W takim przypadku wierzchołek 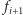 będzie tym wyróżnionym dzieckiem wierzchołka
będzie tym wyróżnionym dzieckiem wierzchołka 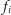 i dostanie swój należny przydział agentów (reguła (ii)). Zauważmy, że
i dostanie swój należny przydział agentów (reguła (ii)). Zauważmy, że 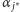 jest iloczynem
jest iloczynem 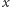 i pewnej liczby czynników nie większych od
i pewnej liczby czynników nie większych od 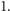 Skoro
Skoro 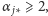 to co najwyżej
to co najwyżej 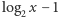 z tych czynników może być nie większych niż
z tych czynników może być nie większych niż 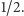 Agenci, którzy wyruszyli z korzenia w rundzie
Agenci, którzy wyruszyli z korzenia w rundzie 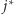 i podążali ścieżką
i podążali ścieżką 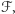 zostali "zaokrągleni w dół" co najwyżej
zostali "zaokrągleni w dół" co najwyżej 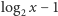 razy. Stąd da się już łatwo wykazać, że z grupy, która wyruszyła w rundzie
razy. Stąd da się już łatwo wykazać, że z grupy, która wyruszyła w rundzie 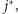 co najmniej jeden agent dotrze do liścia
co najmniej jeden agent dotrze do liścia 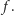 Jeżeli wypuścimy z korzenia co najmniej
Jeżeli wypuścimy z korzenia co najmniej 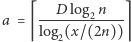 grup agentów, to jedna z nich wyeksploruje dowolnie wybrany liść
grup agentów, to jedna z nich wyeksploruje dowolnie wybrany liść 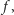 czyli
czyli 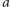 grup wyeksploruje całe drzewo. Całkowity czas eksploracji to
grup wyeksploruje całe drzewo. Całkowity czas eksploracji to 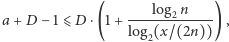 ponieważ tyle rund potrzeba, żeby
ponieważ tyle rund potrzeba, żeby  -ta grupa dotarła do liści. Łączna liczba użytych agentów to co najwyżej
-ta grupa dotarła do liści. Łączna liczba użytych agentów to co najwyżej 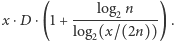 Ustalając
Ustalając 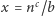 dla odpowiednio dobranej stałej
dla odpowiednio dobranej stałej 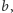 dostajemy:
dostajemy:
Twierdzenie. Dla dowolnego ustalonego 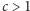 i znanego
i znanego  problem eksploracji drzew może być rozwiązany w czasie
problem eksploracji drzew może być rozwiązany w czasie 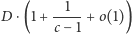 przy użyciu
przy użyciu 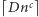 agentów.
agentów.
Notacja 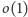 oznacza funkcję, która dąży do 0 dla
oznacza funkcję, która dąży do 0 dla 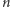 dążącego do nieskończoności. Zauważmy, że znajomość
dążącego do nieskończoności. Zauważmy, że znajomość 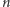 jest potrzebna algorytmowi jedynie do podziału zespołu wszystkich
jest potrzebna algorytmowi jedynie do podziału zespołu wszystkich 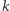 agentów na grupy po
agentów na grupy po 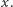 Da się skonstruować algorytm, który eksploruje w czasie
Da się skonstruować algorytm, który eksploruje w czasie 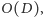 bez znajomości
bez znajomości 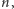 używając
używając 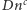 agentów.
agentów.
Uwagi końcowe
- Można wykazać, że nie da się eksplorować szybciej niż w czasie
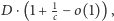 czyli jesteśmy już dość blisko optymalnego algorytmu.
czyli jesteśmy już dość blisko optymalnego algorytmu. - Algorytm można uogólnić na dwa sposoby. Można przerobić na wersję rozproszoną, gdzie agenci podejmują suwerenne decyzje, bazując na swojej wiedzy, i mogą się komunikować z innymi agentami będącymi w tym samym wierzchołku. Można też w ten sposób eksplorować dowolne grafy. Co ciekawe, oba uogólnienia nie dodają zbyt dużo do czasu eksploracji, czyli cała trudność problemu leżała w "centralnie sterowanej" eksploracji drzew.
- Czytelników, którzy zastanawiają się, czy to podejście da się zastosować dla mniejszej grupy agentów, gorąco zachęcam do próbowania.