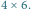Informatyczny kącik olimpijski
Filary
W tym kąciku omówimy zadanie Filary, które pojawiło się na Akademickich Mistrzostwach Polski w Programowaniu Zespołowym 2014. Zadanie, pomimo prostej treści i (jak się za chwilę przekonamy) całkiem prostego rozwiązania, sprawiło sporo kłopotów drużynom startującym w zawodach i ostatecznie zostało rozwiązane tylko przez jedną z nich.

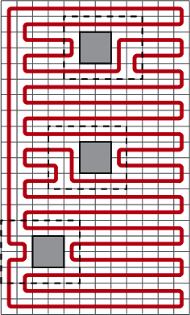
Rys. 1 Z prostokąta 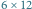 wycięto dwa kwadraty
wycięto dwa kwadraty 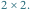 Kolorem zaznaczono przykładowy cykl spełniający warunki zadania.
Kolorem zaznaczono przykładowy cykl spełniający warunki zadania.
Zadanie. Dany jest prostokąt o parzystych wymiarach 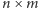 podzielony na
podzielony na 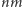 kwadratów jednostkowych, z którego wycięto
kwadratów jednostkowych, z którego wycięto 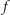 kwadratów
kwadratów 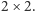 Wycięte kwadraty nie są rozmieszczone zbyt gęsto - środki każdych dwóch kwadratów są odległe o co najmniej 6, a ponadto środek każdego kwadratu jest oddalony o co najmniej 3 od brzegu prostokąta. Należy znaleźć cykl przechodzący dokładnie raz przez wszystkie niewycięte kwadraty jednostkowe (patrz Rys. 1).
Wycięte kwadraty nie są rozmieszczone zbyt gęsto - środki każdych dwóch kwadratów są odległe o co najmniej 6, a ponadto środek każdego kwadratu jest oddalony o co najmniej 3 od brzegu prostokąta. Należy znaleźć cykl przechodzący dokładnie raz przez wszystkie niewycięte kwadraty jednostkowe (patrz Rys. 1).
Powyższe zadanie może być wyrażone w języku teorii grafów. Jeśli rozważymy graf, w którym wierzchołkami są nieusunięte kwadraty jednostkowe, a krawędzie łączą kwadraty jednostkowe mające wspólny bok, to zadanie polega na znalezieniu w tym grafie cyklu Hamiltona (czyli takiego, który przechodzi przez każdy wierzchołek dokładnie raz). Nie jest tajemnicą, że w pełnej ogólności (tzn. jeśli chcemy znaleźć algorytm dający rozwiązanie dla dowolnego grafu) jest to problem NP-zupełny, nie jest więc znane jego efektywne rozwiązanie. Musimy więc skorzystać z tego, że graf z naszego zadania ma specjalną postać. (W szczególności jest planarny, ale to nam nie wystarczy, gdyż znajdowanie cyklu Hamiltona w dowolnym grafie planarnym jest również NP-zupełne.)

Rys. 2 W każdym z 16 niewyciętych kawałków umieszczamy cykl. Drzewo rozpinające grafu kawałków zaznaczono pogrubionymi czarnymi krawędziami.
Na początek rozważmy prostszy wariant zadania, w którym środek każdego wyciętego kwadratu jest odległy od brzegów prostokąta o nieparzystą liczbę. Innymi słowy, jeśli posklejamy wszystkie kwadraty jednostkowe w kawałki o rozmiarach 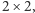 to każdy z takich kawałków będzie w całości wycięty lub nie. W każdym niewyciętym kawałku umieszczamy cykl o długości 4 (Rys. 2). Następnie tworzymy graf, którego wierzchołkami są kawałki (połączone krawędzią, jeśli mają wspólny bok) i znajdujemy w nim dowolne drzewo rozpinające. Porównując oba rysunki, nietrudno zauważyć, jak za pomocą tego drzewa połączyć małe cykle, by dały rozwiązanie. Złożoność czasowa rozwiązania to
to każdy z takich kawałków będzie w całości wycięty lub nie. W każdym niewyciętym kawałku umieszczamy cykl o długości 4 (Rys. 2). Następnie tworzymy graf, którego wierzchołkami są kawałki (połączone krawędzią, jeśli mają wspólny bok) i znajdujemy w nim dowolne drzewo rozpinające. Porównując oba rysunki, nietrudno zauważyć, jak za pomocą tego drzewa połączyć małe cykle, by dały rozwiązanie. Złożoność czasowa rozwiązania to 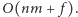

Rys. 3 Otoczenie wyciętego kwadratu cyklem w kawałkach 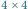 i
i 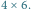

Rys. 4 Początkowe wypełnienie pełnego prostokąta w drugim rozwiązaniu.
Rozwiązując zadanie bez uproszczeń, będziemy musieli dopuścić podział prostokąta na trochę mniej regularne kawałki. Wycięte kwadraty odległe od brzegów prostokąta o parzystą liczbę umieścimy w kawałkach rozmiaru 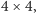 natomiast wycięte kwadraty odległe od brzegów o liczby o różnej parzystości umieścimy w kawałkach
natomiast wycięte kwadraty odległe od brzegów o liczby o różnej parzystości umieścimy w kawałkach 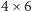 lub
lub 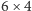 (Rys. 3). Założenia o odległościach pomiędzy środkami wyciętych kwadratów wystarczają do tego, aby nasze kawałki nie nachodziły na siebie. Dalsza część rozwiązania z budowaniem drzewa rozpinającego i łączeniem cykli jest analogiczna.
(Rys. 3). Założenia o odległościach pomiędzy środkami wyciętych kwadratów wystarczają do tego, aby nasze kawałki nie nachodziły na siebie. Dalsza część rozwiązania z budowaniem drzewa rozpinającego i łączeniem cykli jest analogiczna.
Zadanie ma prostsze rozwiązanie. Na początek wypełniamy pełny prostokąt "kaloryferem", jak na rysunku 4 (cykl przechodzi przez kwadraty jednostkowe położone wzdłuż lewego brzegu, a następnie kolejnymi wierszami, zmieniając kierunek).
Rys. 5 Trzy przypadki lokalnych poprawek "kaloryfera".
Następnie wycinamy kolejne kwadraty, za każdym razem poprawiając cykl lokalnie. Na rysunku 5 są przedstawione trzy przypadki, które musimy w tym celu rozważyć. W pierwszym z nich odległość środka wyciętego kwadratu od górnego brzegu prostokąta jest nieparzysta, w pozostałych przypadkach jest parzysta (ostatni przypadek występuje, gdy odległość od lewego brzegu jest równa 3).
Co ciekawe, jeśli zwiększymy do 4 minimalną odległość środków wyciętych kwadratów od brzegów prostokąta, to rozwiązanie stanie się jeszcze prostsze i nie tylko dlatego, że odpadnie nam trzeci przypadek, ale też z uwagi na alternatywną implementację. Wycinamy wszystkie kwadraty, a następnie, zaczynając od lewego dolnego rogu, budujemy cykl zachłannie, zawsze wykonując pierwszy możliwy ruch z następującej listy: góra, prawo, lewo, dół. Czytelnicy zechcą sprawdzić, że dla prostokąta z rysunku 5 (w którym nie wycinamy dolnego kwadratu) algorytm lokalnie poprawiający cykl i algorytm zachłanny dają taki sam wynik.
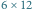 wycięto dwa kwadraty
wycięto dwa kwadraty 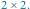 Kolorem zaznaczono przykładowy cykl spełniający warunki zadania.
Kolorem zaznaczono przykładowy cykl spełniający warunki zadania.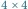 i
i