Słowa pierwsze

W numerze 10/2010 Delty pojawił się artykuł Wojciecha Plandowskiego, w którym autor po ciężkich bojach pokazuje rozwiązanie pewnego konkretnego typu równania na słowach. Mogłoby się wydawać: udało się, sprawa skończona. Tymczasem przy okazji w artykule pojawia się definicja i kilka ważnych własności słów pierwotnych, a stąd już tylko mały krok do innej ciekawej rodziny słów, mianowicie do słów pierwszych. To dobry pretekst, by coś o nich opowiedzieć.

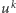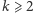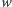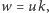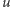Przypomnijmy, że słowo pierwotne to takie, które nie jest potęgą ( $| k u$ dla $|k⩾ 2$ ) żadnego niepustego słowa. Znamy już kilka własności takich słów, w szczególności to, że każde słowo $w$ przedstawia się jednoznacznie w postaci $|w= uk,$ gdzie $u$ jest pierwotne; w tym artykule będzie nam wygodnie nazwać $| u$ pierwiastkiem pierwotnym słowa 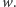$| w.$ Dalej, wiemy, że każdy obrót cykliczny słowa pierwotnego jest pierwotny, a dodatkowo wszystkie takie obroty stanowią różne słowa. Wśród tych obrotów jedno słowo jest, w szczególności, najmniejsze leksykograficznie, tj. najmniejsze w porządku słownikowym. Każde takie słowo pierwotne najmniejsze w klasie swoich obrotów cyklicznych nazwiemy właśnie słowem pierwszym (inna nazwa: słowo Lyndona). Kilka przykładów słów pierwszych: 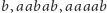$b,aabab, aaaab$ oraz niepierwszych: 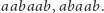$|aabaab, abaab.$ Zanim wyjaśnimy nieco tajemniczą nazwę rozważanej rodziny słów, przyjrzyjmy się następującej, równoważnej definicji słów pierwszych:

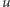Twierdzenie 1. Niepuste słowo $u$ jest pierwsze wtedy i tylko wtedy, gdy każdy właściwy sufiks $| u$ (czyli końcowy fragment różny od $| u$ i od słowa pustego jest leksykograficznie większy niż $u.$

Cały artykuł dostępny jest w wersji do druku [application/pdf]: (369 KB)