O rozkładzie słów na słowa Lyndona

W tym artykule rozwiążemy problem rozkładu słowa na najmniejszą liczbę słów Lyndona (zwanych też słowami pierwszymi). Problem ten jest inspirowany zadaniem Jan z pierwszej edycji Potyczek Algorytmicznych, która odbyła się w roku 2005.

Jakub Radoszewski w artykule Słowa pierwsze, Delta 12/2010, podał kluczowe własności słów Lyndona, które wykorzystamy podczas konstrukcji algorytmu. Przypomnijmy, że słowo Lyndona to takie słowo, że przy dowolnym jego obrocie cyklicznym zawsze otrzymuje się słowo późniejsze od niego leksykograficznie. Obrót cykliczny polega na przeniesieniu początkowego fragmentu słowa na jego koniec, np. dla słowa 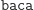$|baca$ mamy następujące obroty: 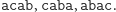$|acab,caba, abac.$ Oczywiście słowo 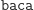$|baca$ nie jest słowem Lyndona, gdyż 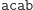$|acab$ występuje wcześniej w słowniku. Słowo 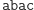$abac$ jest już słowem Lyndona.

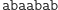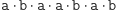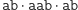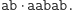
Słowo $|abaabab$ również nie jest słowem Lyndona, ale można je rozłożyć na słowa Lyndona. Trywialny jest rozkład na słowa jednoliterowe $|a⋅b ⋅a⋅a ⋅b⋅a ⋅b$ (przy czym $⋅$ oznacza sklejenie słów), ale istnieją też bardziej oszczędne rozkłady, np. $ab ⋅aab ⋅ab$ lub $ab ⋅aabab.$

Dalej skorzystamy z trzech twierdzeń. Opisują one znane własności słów Lyndona. Dowody tych twierdzeń można znaleźć w przywołanym artykule z Delty 12/2010.

Cały artykuł dostępny jest w wersji do druku [application/pdf]: (253 KB)