Informatyczny kącik olimpijski
Trasowanie
Tym razem zajmiemy się zadaniem Routing z finałów Akademickich Mistrzostw Świata w Programowaniu Zespołowym z 2006 roku...
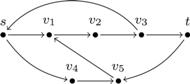
Rys. 1 Optymalne rozwiązanie dla powyższego grafu to
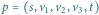 i
i
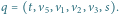 Ścieżki przechodzą łącznie przez 6 wierzchołków.
Ścieżki przechodzą łącznie przez 6 wierzchołków.
Po przetłumaczeniu historyjki o sieci komputerowej na język
teorii grafów brzmi ono następująco. Dany jest skierowany graf
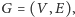 mający
mający
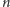 wierzchołków, z których wyróżniamy
początkowy
wierzchołków, z których wyróżniamy
początkowy
 i końcowy
i końcowy
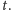 Chcemy znaleźć
w grafie
Chcemy znaleźć
w grafie
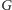 dwie skierowane ścieżki
dwie skierowane ścieżki
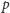 i
i
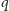 (pierwszą
z
(pierwszą
z
 do
do
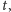 a drugą z
a drugą z
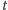 do
do
 ) tak, by łączna liczba
wierzchołków, przez które przechodzą te ścieżki, była jak najmniejsza
(Rys. 1).
) tak, by łączna liczba
wierzchołków, przez które przechodzą te ścieżki, była jak najmniejsza
(Rys. 1).
W rozwiązaniu będziemy konstruowali obie ścieżki, poruszając się
od wierzchołka
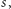 dla pierwszej z nich zgodnie ze skierowaniem krawędzi,
a dla drugiej – przeciwnie. Zdefiniujmy w tym celu ważony graf skierowany
dla pierwszej z nich zgodnie ze skierowaniem krawędzi,
a dla drugiej – przeciwnie. Zdefiniujmy w tym celu ważony graf skierowany
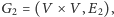 w którym z wierzchołka
w którym z wierzchołka
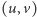 wychodzą
krawędzie:
wychodzą
krawędzie:
- (1)
- (1) do
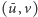 o wadze
o wadze
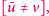 jeśli
jeśli
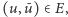
- (2)
- (2) do
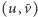 o wadze
o wadze
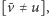 jeśli
jeśli
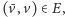
- (3)
- (3) do
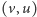 o wadze
o wadze
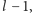 jeśli w
jeśli w
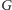 istnieje
skierowana ścieżka z
istnieje
skierowana ścieżka z
 do
do
 i najkrótsza taka
ścieżka zawiera
i najkrótsza taka
ścieżka zawiera
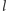 krawędzi.
krawędzi.
Krawędzie (1) i (2) w
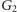 odpowiadają przesuwaniu się
ścieżką
odpowiadają przesuwaniu się
ścieżką
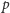 w
w
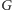 zgodnie ze skierowaniem krawędzi
i ścieżką
zgodnie ze skierowaniem krawędzi
i ścieżką
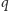 przeciwnie do skierowania krawędzi. Natomiast krawędź (3)
w
przeciwnie do skierowania krawędzi. Natomiast krawędź (3)
w
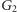 odpowiada przesunięciu się obiema ścieżkami po tych samych
krawędziach w
odpowiada przesunięciu się obiema ścieżkami po tych samych
krawędziach w
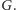 Łatwo się więc przekonać, że jeżeli w
Łatwo się więc przekonać, że jeżeli w
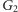 istnieje
ścieżka z
istnieje
ścieżka z
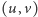 do
do
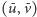 o wadze
o wadze
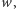 to oznacza, że
w
to oznacza, że
w
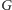 istnieją dwie ścieżki, pierwsza z
istnieją dwie ścieżki, pierwsza z
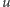 do
do
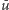 i druga
z
i druga
z
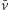 do
do
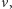 takie że sumaryczna liczba wierzchołków,
przez jakie przechodzą (nie licząc
takie że sumaryczna liczba wierzchołków,
przez jakie przechodzą (nie licząc
 i
i
 ), jest
równa co najwyżej
), jest
równa co najwyżej
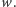 W szczególności, ścieżka
w
W szczególności, ścieżka
w
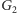 z
z
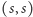 do
do
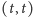 o wadze
o wadze
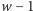 implikuje
istnienie rozwiązania zadania o koszcie
implikuje
istnienie rozwiązania zadania o koszcie
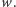
Pozostaje nam wykazać, że jeśli w optymalnym rozwiązaniu ścieżki
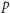 i
i
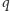 przechodzą przez
przechodzą przez
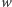 wierzchołków, to w grafie
wierzchołków, to w grafie
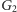 istnieje
ścieżka z
istnieje
ścieżka z
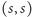 do
do
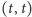 o wadze
o wadze
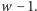 Niech
Niech
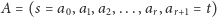 będzie listą wierzchołków
wspólnych dla obu ścieżek w kolejności, w jakiej te wierzchołki występują
na ścieżce
będzie listą wierzchołków
wspólnych dla obu ścieżek w kolejności, w jakiej te wierzchołki występują
na ścieżce
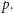 Powiemy, że wierzchołki
Powiemy, że wierzchołki
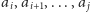 tworzą
blok, jeśli są one odwiedzane w tej kolejności również przez
ścieżkę
tworzą
blok, jeśli są one odwiedzane w tej kolejności również przez
ścieżkę
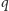 (oznaczymy to przez
(oznaczymy to przez
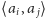 ). Zauważmy, że
z optymalności ścieżek
). Zauważmy, że
z optymalności ścieżek
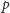 i
i
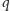 wynika, że na każdej
ze ścieżek między wierzchołkami należącymi do tego samego bloku
nie występują wierzchołki spoza
wynika, że na każdej
ze ścieżek między wierzchołkami należącymi do tego samego bloku
nie występują wierzchołki spoza
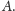 Podobny argument dowodzi tego,
że jeśli ścieżka
Podobny argument dowodzi tego,
że jeśli ścieżka
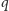 odwiedza wierzchołek
odwiedza wierzchołek
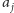 jako najbliższy
wierzchołek z
jako najbliższy
wierzchołek z
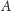 po wierzchołku
po wierzchołku
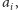 to
to
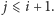 Jeśli
więc
Jeśli
więc
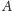 podzielimy na maksymalne bloki w kolejności ich odwiedzania
przez ścieżkę
podzielimy na maksymalne bloki w kolejności ich odwiedzania
przez ścieżkę
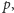 to ścieżka
to ścieżka
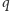 będzie je odwiedzać
w odwrotnej kolejności. Ponadto pierwszy i ostatni blok podziału będą to
odpowiednio
będzie je odwiedzać
w odwrotnej kolejności. Ponadto pierwszy i ostatni blok podziału będą to
odpowiednio
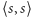 i
i
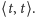
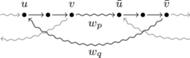
Rys. 2
Pokażemy (Rys. 2), że dla kolejnych dwóch bloków
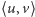 i
i
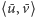 tego
podziału istnieje ścieżka w grafie
tego
podziału istnieje ścieżka w grafie
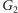 z
z
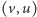 do
do
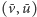 o wadze
o wadze
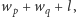 gdzie
gdzie
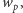
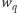 to odpowiednio liczby wierzchołków
spoza
to odpowiednio liczby wierzchołków
spoza
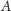 odwiedzanych przez ścieżkę
odwiedzanych przez ścieżkę
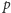 od
od
 do
do
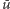 oraz
przez ścieżkę
oraz
przez ścieżkę
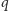 od
od
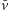 do
do
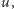 natomiast
natomiast
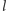 to rozmiar
bloku
to rozmiar
bloku
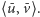 Istotnie, z
Istotnie, z
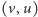 do
do
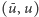 przechodzimy
przechodzimy
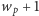 krawędziami (1), następnie z
krawędziami (1), następnie z
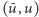 do
do
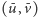 przechodzimy
przechodzimy
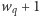 krawędziami (2) o łącznej wadze
krawędziami (2) o łącznej wadze
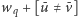 i ostatecznie
(jeśli
i ostatecznie
(jeśli
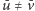 ) używamy krawędzi (3) o wadze
) używamy krawędzi (3) o wadze
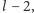 aby dostać
się z
aby dostać
się z
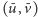 do
do
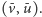 W ten sposób konstruujemy ścieżkę
w
W ten sposób konstruujemy ścieżkę
w
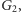 która odwiedza wszystkie bloki i ma wagę równą
która odwiedza wszystkie bloki i ma wagę równą
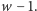

Tak więc dowiedliśmy, że aby znaleźć rozwiązanie, wystarczy, że wyznaczymy
najlżejszą ścieżkę z
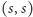 do
do
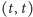 w grafie
w grafie
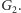 Możemy to
zrobić algorytmem Dijkstry, na bieżąco konstruując graf
Możemy to
zrobić algorytmem Dijkstry, na bieżąco konstruując graf
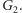 Za każdym
razem, gdy z kolejki priorytetowej wyciągamy wierzchołek
Za każdym
razem, gdy z kolejki priorytetowej wyciągamy wierzchołek
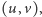 przechodzimy
po liście sąsiedztwa
przechodzimy
po liście sąsiedztwa
 w
w
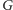 i relaksujemy krawędzie (1),
następnie przechodzimy po liście sąsiedztwa
i relaksujemy krawędzie (1),
następnie przechodzimy po liście sąsiedztwa
 w grafie
transponowanym
w grafie
transponowanym
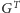 i relaksujemy krawędzie (2); w końcu
sprawdzamy, czy
i relaksujemy krawędzie (2); w końcu
sprawdzamy, czy
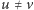 i jeśli tak, relaksujemy krawędź (3).
i jeśli tak, relaksujemy krawędź (3).
Graf
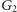 ma
ma
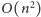 wierzchołków. Każdy z nich jest początkiem
wierzchołków. Każdy z nich jest początkiem
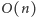 krawędzi (1) i (2) i co najwyżej jednej krawędzi (3), zatem
w
krawędzi (1) i (2) i co najwyżej jednej krawędzi (3), zatem
w
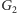 mamy
mamy
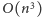 krawędzi. Ponadto uaktualnienie wagi
wierzchołka podczas relaksacji będzie wykonywane tylko
krawędzi. Ponadto uaktualnienie wagi
wierzchołka podczas relaksacji będzie wykonywane tylko
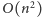 razy,
gdyż krawędzie wchodzące do każdego wierzchołka w
razy,
gdyż krawędzie wchodzące do każdego wierzchołka w
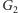 mają
co najwyżej trzy różne wagi. Zatem złożoność czasowa rozwiązania
wyniesie
mają
co najwyżej trzy różne wagi. Zatem złożoność czasowa rozwiązania
wyniesie
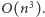 Tyle też będzie trwało obliczenie długości
najkrótszych ścieżek pomiędzy wszystkimi parami wierzchołków
w
Tyle też będzie trwało obliczenie długości
najkrótszych ścieżek pomiędzy wszystkimi parami wierzchołków
w
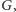 jeśli użyjemy do tego algorytmu Floyda–Warshalla.
jeśli użyjemy do tego algorytmu Floyda–Warshalla.
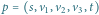 i
i
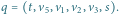 Ścieżki przechodzą łącznie przez 6 wierzchołków.
Ścieżki przechodzą łącznie przez 6 wierzchołków.
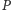 nawias Iversona
nawias Iversona
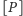 jest zdefiniowany
następująco:
jest zdefiniowany
następująco:
