Informatyczny kącik olimpijski
Świetliki
Tym razem w kąciku zadanie Świetliki, z którym mierzyli się finaliści Potyczek Algorytmicznych 2013.
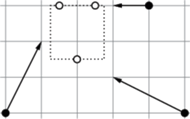
Czarne kropki to trzy świetliki znajdujące się w chwili
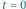 w punktach
w punktach
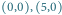 i
i
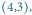 poruszające się z prędkościami
poruszające się z prędkościami
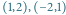 i
i
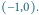 Zaznaczono
też kwadrat o minimalnym boku
Zaznaczono
też kwadrat o minimalnym boku
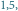 w którym znajdą się świetliki w chwili
w którym znajdą się świetliki w chwili
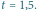
Problem. Po płaszczyźnie porusza się
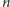 świetlików. Dla każdego
z owadów znamy punkt płaszczyzny, w którym znajdował się początkowo,
oraz wiemy, że porusza się on ze stałym (i znanym nam) wektorem
prędkości. Należy wyznaczyć minimalną długość, jaką może mieć
bok kwadratu, który będzie w pewnej chwili zawierał wszystkie świetliki,
przy czym boki kwadratu muszą być ustawione równolegle do osi układu
współrzędnych (rysunek).
świetlików. Dla każdego
z owadów znamy punkt płaszczyzny, w którym znajdował się początkowo,
oraz wiemy, że porusza się on ze stałym (i znanym nam) wektorem
prędkości. Należy wyznaczyć minimalną długość, jaką może mieć
bok kwadratu, który będzie w pewnej chwili zawierał wszystkie świetliki,
przy czym boki kwadratu muszą być ustawione równolegle do osi układu
współrzędnych (rysunek).
Oznaczmy jeszcze przez
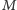 ograniczenie na zakres liczb danych
w zadaniu. Zacznijmy od wykorzystania technik standardowych przy tego typu
zadaniach. Bok kwadratu możemy wyznaczyć, stosując wyszukiwanie binarne,
zatem
ograniczenie na zakres liczb danych
w zadaniu. Zacznijmy od wykorzystania technik standardowych przy tego typu
zadaniach. Bok kwadratu możemy wyznaczyć, stosując wyszukiwanie binarne,
zatem
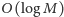 razy będziemy musieli odpowiedzieć na pytanie „czy
istnieje taka chwila
razy będziemy musieli odpowiedzieć na pytanie „czy
istnieje taka chwila
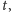 że wszystkie świetliki zmieszczą się w kwadracie
o boku
że wszystkie świetliki zmieszczą się w kwadracie
o boku
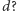 ”.
”.
Kolejne standardowe spostrzeżenie: istnieje optymalne rozwiązanie, w którym
skrajnie lewy świetlik znajduje się na lewym boku kwadratu. Dla ustalonego
świetlika
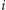 możemy w czasie
możemy w czasie
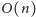 wyznaczyć przedział
czasu, w którym znajduje się on po lewej stronie od każdego innego
świetlika. Ograniczywszy się do tego przedziału czasu, unieruchamiamy tego
świetlika, zaczepiając w nim układ współrzędnych (tzn. odejmujemy jego
prędkość i pozycję od prędkości i pozycji wszystkich pozostałych
świetlików).
wyznaczyć przedział
czasu, w którym znajduje się on po lewej stronie od każdego innego
świetlika. Ograniczywszy się do tego przedziału czasu, unieruchamiamy tego
świetlika, zaczepiając w nim układ współrzędnych (tzn. odejmujemy jego
prędkość i pozycję od prędkości i pozycji wszystkich pozostałych
świetlików).
Znamy bok i położenie kwadratu w poziomie, musimy teraz sprawdzić,
czy istnieje taka chwila
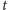 i takie jego położenie w pionie
i takie jego położenie w pionie
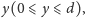 które zawiera wszystkie owady. Nietrudno się przekonać,
że dla ustalonego świetlika zbiór punktów
które zawiera wszystkie owady. Nietrudno się przekonać,
że dla ustalonego świetlika zbiór punktów
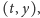 dla których
świetlik ten znajduje się w chwili
dla których
świetlik ten znajduje się w chwili
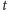 w kwadracie przesuniętym
o
w kwadracie przesuniętym
o
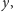 jest równoległobokiem. A konkretnie: jeśli świetlik
jest równoległobokiem. A konkretnie: jeśli świetlik
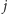 znajduje się w punkcie
znajduje się w punkcie
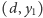 w chwili
w chwili
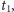 a w punkcie
a w punkcie
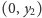 w chwili
w chwili
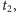 to wierzchołkami szukanego równoległoboku
są punkty
to wierzchołkami szukanego równoległoboku
są punkty
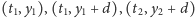 i
i
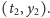 Wyznaczenie
równoległoboków dla wszystkich owadów zajmie nam czas
Wyznaczenie
równoległoboków dla wszystkich owadów zajmie nam czas
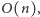 a następnie sprawdzenie, czy ich przecięcie jest niepuste – czas
a następnie sprawdzenie, czy ich przecięcie jest niepuste – czas
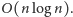
Ostatecznie nasze rozwiązanie działa w czasie
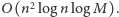
Istnieje szybsze (i prostsze do zaimplementowania) rozwiązanie działające
w czasie
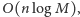 wymaga ono jednak pewnej nie do końca
oczywistej obserwacji. Oznaczmy przez
wymaga ono jednak pewnej nie do końca
oczywistej obserwacji. Oznaczmy przez
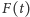 najmniejszy bok kwadratu
dla ustalonej chwili
najmniejszy bok kwadratu
dla ustalonej chwili
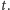 Czy możemy coś powiedzieć o funkcji
Czy możemy coś powiedzieć o funkcji
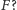 Jasne jest, że powyżej pewnej granicy wraz ze wzrostem wartości
bezwzględnej argumentu
Jasne jest, że powyżej pewnej granicy wraz ze wzrostem wartości
bezwzględnej argumentu
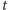 funkcja
funkcja
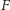 będzie rosnąć. Okazuje się,
że możemy powiedzieć dużo więcej – funkcja
będzie rosnąć. Okazuje się,
że możemy powiedzieć dużo więcej – funkcja
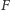 jest wypukła. Dzięki
temu możemy znaleźć jej minimum, stosując wyszukiwanie ternarne, co
będzie wymagało obliczenia jej wartości w
jest wypukła. Dzięki
temu możemy znaleźć jej minimum, stosując wyszukiwanie ternarne, co
będzie wymagało obliczenia jej wartości w
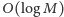 punktach. Dla
ustalonego
punktach. Dla
ustalonego
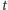 obliczenie
obliczenie
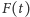 jest bardzo proste (wyznaczamy
pozycje świetlików i znajdujemy prostokąt otaczający) i wymaga czasu
jest bardzo proste (wyznaczamy
pozycje świetlików i znajdujemy prostokąt otaczający) i wymaga czasu
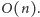 Musimy tylko pamiętać, że rozwiązaniem zadania jest
Musimy tylko pamiętać, że rozwiązaniem zadania jest
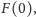 jeśli minimum
jeśli minimum
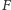 znajdzie się w punkcie
znajdzie się w punkcie
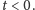
Pozostaje udowodnić kluczowy fakt o wypukłości funkcji
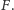 Oznaczmy
przez
Oznaczmy
przez
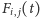 rozmiar najmniejszego kwadratu zawierającego świetliki
rozmiar najmniejszego kwadratu zawierającego świetliki
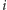 oraz
oraz
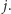 Ponieważ w każdej chwili wynikowy kwadrat opiera się
na dwóch świetlikach po jego przeciwnych stronach, to
Ponieważ w każdej chwili wynikowy kwadrat opiera się
na dwóch świetlikach po jego przeciwnych stronach, to
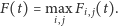 |
Funkcja
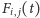 jest wypukła (łatwo to zobaczyć, jeśli znów zaczepimy
układ współrzędnych w świetliku
jest wypukła (łatwo to zobaczyć, jeśli znów zaczepimy
układ współrzędnych w świetliku
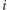 ). Tak więc funkcja
). Tak więc funkcja
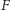 jest
również wypukła, jako maksimum funkcji wypukłych.
jest
również wypukła, jako maksimum funkcji wypukłych.
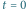 w punktach
w punktach
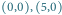 i
i
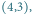 poruszające się z prędkościami
poruszające się z prędkościami
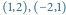 i
i
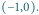 Zaznaczono
też kwadrat o minimalnym boku
Zaznaczono
też kwadrat o minimalnym boku
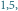 w którym znajdą się świetliki w chwili
w którym znajdą się świetliki w chwili