Informatyczny kącik olimpijski
Drogi Stanowe
Tym razem omówimy zadanie o drogach stanowych (State Roads) z pierwszej rundy zawodów Yandex.Algorithm 2013. Zadanie to można sformułować w języku teorii grafów, a do tego w ujęciu dynamicznym...
Zadanie. Mamy więc graf nieskierowany o zbiorze wierzchołków
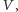 początkowo pusty, w którym w kolejnych
momentach pojawiają się i znikają krawędzie. Pomiędzy takimi zdarzeniami
otrzymujemy zapytania, z których każde dotyczy pewnego podzbioru
wierzchołków grafu
początkowo pusty, w którym w kolejnych
momentach pojawiają się i znikają krawędzie. Pomiędzy takimi zdarzeniami
otrzymujemy zapytania, z których każde dotyczy pewnego podzbioru
wierzchołków grafu
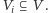 W odpowiedzi na takie zapytanie mamy
stwierdzić, czy z jakiegokolwiek wierzchołka zbioru
W odpowiedzi na takie zapytanie mamy
stwierdzić, czy z jakiegokolwiek wierzchołka zbioru
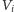 wychodzi
jakaś krawędź poza ten zbiór; innymi słowy, czy wierzchołki zbioru
wychodzi
jakaś krawędź poza ten zbiór; innymi słowy, czy wierzchołki zbioru
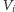 w rozważanym momencie stanowią sumę pewnej liczby spójnych
składowych grafu. W zadaniu występuje też techniczny (ale przyjemny)
warunek, że wstawiane krawędzie otrzymują numery będące kolejnymi
liczbami naturalnymi i za pomocą tych numerów oznaczane są krawędzie
przeznaczone do usunięcia.
w rozważanym momencie stanowią sumę pewnej liczby spójnych
składowych grafu. W zadaniu występuje też techniczny (ale przyjemny)
warunek, że wstawiane krawędzie otrzymują numery będące kolejnymi
liczbami naturalnymi i za pomocą tych numerów oznaczane są krawędzie
przeznaczone do usunięcia.
Zastanówmy się najpierw nad rozwiązaniem siłowym. Tym razem, celowo,
omówimy dość dokładnie nietrywialne szczegóły implementacyjne
rozwiązania. Cały graf możemy przechowywać po prostu jako
tablicę list sąsiedztwa. Przy wstawianiu krawędzi
 o numerze
o numerze
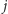 dodajemy po jednym nowym elemencie do list sąsiedztwa
wierzchołków
dodajemy po jednym nowym elemencie do list sąsiedztwa
wierzchołków
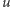 i
i
 i w osobnej tablicy indeksowanej
numerem krawędzi zapamiętujemy wskaźniki na elementy list, które
dodaliśmy dla tej krawędzi. Takie wstawienie działa oczywiście w czasie
stałym:
i w osobnej tablicy indeksowanej
numerem krawędzi zapamiętujemy wskaźniki na elementy list, które
dodaliśmy dla tej krawędzi. Takie wstawienie działa oczywiście w czasie
stałym:
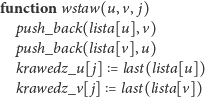
Dzięki wspomnianemu przyjemnemu warunkowi technicznemu uprzednio wstawioną krawędź możemy usunąć z grafu również w czasie stałym, po prostu usuwając odpowiednie elementy list sąsiedztwa:

Bardziej czasochłonną operacją jest, oczywiście, odpowiedź na zapytanie. Wczytując wierzchołki występujące w zapytaniu, możemy równocześnie zaznaczać wszystkie te wierzchołki w pomocniczej tablicy indeksowanej numerami wierzchołków. Żeby nie musieć za każdym razem zerować tej tablicy, wierzchołki z każdego nowego zapytania możemy oznaczać numerem porządkowym tego zapytania. Teraz obsługa zapytania jest już bardzo prosta – przeglądamy kolejne wierzchołki z zapytania, dla każdego z nich przeglądamy wszystkie incydentne krawędzie i sprawdzamy, czy drugie końce tych krawędzi są zaznaczone w tablicy pomocniczej:
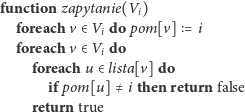
Na pierwszy rzut oka widać, że obsługa zapytania jest tutaj bardzo wolna.
Warto jednak przyjrzeć się temu dokładniej. Przede wszystkim należy
ustalić, co jest dla nas rozmiarem danych wejściowych. Oznaczmy przez
 liczbę wierzchołków grafu, a przez
liczbę wierzchołków grafu, a przez
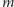 – łączną liczbę krawędzi
wstawionych kiedykolwiek do grafu. Niech
– łączną liczbę krawędzi
wstawionych kiedykolwiek do grafu. Niech
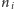 (dla
(dla
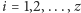 )
oznacza liczbę wierzchołków występujących w
)
oznacza liczbę wierzchołków występujących w
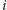 -tym zapytaniu,
-tym zapytaniu,
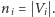 Całkiem naturalnie jako rozmiar danych wejściowych
przyjmiemy
Całkiem naturalnie jako rozmiar danych wejściowych
przyjmiemy
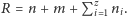
Jak teraz wyrazić względem
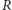 koszt obsługi wszystkich zapytań?
Zauważmy, że w
koszt obsługi wszystkich zapytań?
Zauważmy, że w
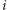 -tym zapytaniu będziemy musieli przejrzeć co
najwyżej
-tym zapytaniu będziemy musieli przejrzeć co
najwyżej
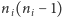 krawędzi. Faktycznie, tyle krawędzi (liczonych
w obie strony) ma klika o
krawędzi. Faktycznie, tyle krawędzi (liczonych
w obie strony) ma klika o
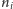 wierzchołkach, więc jeśli w listach
sąsiedztwa wierzchołków z zapytania znajdzie się więcej niż tyle krawędzi, to
na pewno odpowiedź na to zapytanie będzie negatywna. Asymptotycznie daje to
koszt
wierzchołkach, więc jeśli w listach
sąsiedztwa wierzchołków z zapytania znajdzie się więcej niż tyle krawędzi, to
na pewno odpowiedź na to zapytanie będzie negatywna. Asymptotycznie daje to
koszt
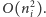 Z drugiej strony, w każdym zapytaniu przejrzymy
łącznie co najwyżej
Z drugiej strony, w każdym zapytaniu przejrzymy
łącznie co najwyżej
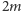 krawędzi. Ostatecznie koszt zapytania to
krawędzi. Ostatecznie koszt zapytania to
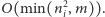 Skorzystajmy teraz z nierówności między minimum
a średnią geometryczną:
Skorzystajmy teraz z nierówności między minimum
a średnią geometryczną:

Całkowity koszt obsługi wszystkich zapytań możemy oszacować przez:

Czyli jednak to rozwiązanie nie było znowuż aż takie wolne!
Jednak da się lepiej. I to dużo lepiej, bowiem liniowo względem rozmiaru
danych wejściowych. Rozwiązanie opiera się na następującym pomyśle:
obliczmy sumę stopni wierzchołków ze zbioru
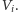 Jeśli suma ta
jest nieparzysta, to na pewno z
Jeśli suma ta
jest nieparzysta, to na pewno z
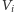 wychodzi jakaś krawędź na
zewnątrz, bowiem w każdym grafie suma stopni wierzchołków jest
parzysta. Pomysł ten w ogólności nie działa – może się okazać, że
suma stopni wierzchołków w
wychodzi jakaś krawędź na
zewnątrz, bowiem w każdym grafie suma stopni wierzchołków jest
parzysta. Pomysł ten w ogólności nie działa – może się okazać, że
suma stopni wierzchołków w
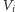 będzie parzysta, a mimo tego
odpowiedź na zapytanie będzie negatywna. Uogólnijmy zatem nasz pomysł
i wprowadźmy element randomizacji. Każdej krawędzi wstawianej do grafu
przypiszmy losową wagę będącą liczbą całkowitą. Dla każdego wierzchołka
będzie parzysta, a mimo tego
odpowiedź na zapytanie będzie negatywna. Uogólnijmy zatem nasz pomysł
i wprowadźmy element randomizacji. Każdej krawędzi wstawianej do grafu
przypiszmy losową wagę będącą liczbą całkowitą. Dla każdego wierzchołka
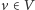 będziemy przechowywać (jako
będziemy przechowywać (jako
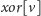 ) bitową alternatywę
wykluczającą wag krawędzi incydentnych z tym wierzchołkiem. Przy
wstawianiu i usuwaniu krawędzi tablicę
) bitową alternatywę
wykluczającą wag krawędzi incydentnych z tym wierzchołkiem. Przy
wstawianiu i usuwaniu krawędzi tablicę
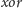 możemy aktualizować
w czasie stałym – w obu przypadkach wystarczy do-xor-ować wagę
krawędzi do
możemy aktualizować
w czasie stałym – w obu przypadkach wystarczy do-xor-ować wagę
krawędzi do
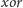 -ów jej końców. W przypadku wstawiania będzie
to:
-ów jej końców. W przypadku wstawiania będzie
to:

Kluczowa obserwacja jest teraz taka: odpowiedź na zapytanie
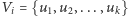 jest pozytywna wtedy i tylko wtedy, gdy każda
krawędź w grafie jest incydentna z dwoma wierzchołkami ze zbioru
jest pozytywna wtedy i tylko wtedy, gdy każda
krawędź w grafie jest incydentna z dwoma wierzchołkami ze zbioru
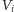 lub z żadnym z nich. Ponieważ
lub z żadnym z nich. Ponieważ
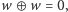 zatem aby
odpowiedzieć na zapytanie, obliczamy wartość:
zatem aby
odpowiedzieć na zapytanie, obliczamy wartość:

Jeśli powyższa wartość jest różna od zera, na pewno odpowiedź na
zapytanie jest negatywna. W przeciwnym razie z dużym prawdopodobieństwem
odpowiedź jest pozytywna. Prawdopodobieństwo udzielenia błędnej
odpowiedzi, czyli trafienia przypadkiem na 0, wynosi
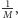 gdzie
gdzie
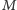 jest ograniczeniem górnym na wagę krawędzi. Przyjmując, naturalnie,
jest ograniczeniem górnym na wagę krawędzi. Przyjmując, naturalnie,
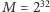 lub
lub
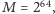 otrzymujemy rzeczywiście bardzo małe
prawdopodobieństwo błędu.
otrzymujemy rzeczywiście bardzo małe
prawdopodobieństwo błędu.