Informatyczny kącik olimpijski
Karty
W tym kąciku zmierzymy się z zadaniem Karty z Potyczek Algorytmicznych 2013. Oryginalne sformułowanie zadania dotyczyło kart perforowanych, my jednak przedstawimy je nieco inaczej, przy okazji wprowadzając niejawnie kilka nieznaczących uproszczeń.
Dana jest kartka w kratkę rozmiaru
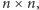 której część pól jest
dozwolonych, a część zabronionych. Będziemy chcieli pokryć wszystkie
pola dozwolone, używając do tego celu prostokątnej pieczątki o jak
największym polu. Każde pole dozwolone możemy pokryć wielokrotnie,
natomiast nie możemy nigdy położyć pieczątki na żadnym polu
zabronionym. Pieczątka nie może w żadnym momencie wyjść poza
obręb kartki – możemy założyć, że kartka jest otoczona kwadratową
obwódką złożoną z pól zabronionych. Pieczątki nie można też
obracać.
której część pól jest
dozwolonych, a część zabronionych. Będziemy chcieli pokryć wszystkie
pola dozwolone, używając do tego celu prostokątnej pieczątki o jak
największym polu. Każde pole dozwolone możemy pokryć wielokrotnie,
natomiast nie możemy nigdy położyć pieczątki na żadnym polu
zabronionym. Pieczątka nie może w żadnym momencie wyjść poza
obręb kartki – możemy założyć, że kartka jest otoczona kwadratową
obwódką złożoną z pól zabronionych. Pieczątki nie można też
obracać.
Zacznijmy od rozwiązania siłowego. Chcemy dla każdego prostokąta
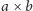 sprawdzić, czy opisuje on poprawną pieczątkę. W tym celu na
wszystkie możliwe sposoby spróbujemy przyłożyć ten prostokąt do
kartki. Tak więc dla każdego pola
sprawdzić, czy opisuje on poprawną pieczątkę. W tym celu na
wszystkie możliwe sposoby spróbujemy przyłożyć ten prostokąt do
kartki. Tak więc dla każdego pola
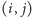 kartki sprawdzimy, czy
prostokąt
kartki sprawdzimy, czy
prostokąt
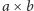 o lewym górnym rogu w tym polu zawiera tylko pola
dozwolone, a jeśli tak, zaznaczymy wszystkie te pola jako pokryte. Wszystkich
prostokątów jest
o lewym górnym rogu w tym polu zawiera tylko pola
dozwolone, a jeśli tak, zaznaczymy wszystkie te pola jako pokryte. Wszystkich
prostokątów jest
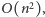 możliwych przyłożeń prostokąta również
możliwych przyłożeń prostokąta również
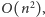 wreszcie sprawdzenie poprawności przyłożenia i pokrycie
przypieczętowanych pól zajmuje czas
wreszcie sprawdzenie poprawności przyłożenia i pokrycie
przypieczętowanych pól zajmuje czas
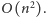 Łącznie rozwiązanie to
działa w niezbyt ciekawej złożoności czasowej
Łącznie rozwiązanie to
działa w niezbyt ciekawej złożoności czasowej
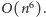
Za pomocą dosyć standardowych technik można takie rozwiązanie
przyspieszyć nawet o kilka rzędów złożoności. Zaczniemy od tzw.
dwuwymiarowych sum prefiksowych, czyli metody znanej z zadania Mapy
gęstości z VIII Olimpiady Informatycznej. W metodzie tej dla każdego
prostokąta „prefiksowego”, czyli prostokąta zawierającego lewy górny
róg kartki, zapamiętujemy liczbę pól zabronionych w tym prostokącie.
Prostokątów prefiksowych jest, rzecz jasna,
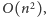 a żądane wartości
możemy wyznaczyć, traktując pola dozwolone jako 1, zabronione jako 0
i dwukrotnie obliczając sumy prefiksowe, najpierw w wierszach, a potem
w kolumnach kartki. Teraz sumę pól w dowolnym prostokącie wyraża się
jako sumę i różnicę co najwyżej czterech wartości dla prostokątów
prefiksowych. W ten sposób sprawdzenie poprawności przyłożenia pieczątki
można zrealizować w czasie stałym. Podobnie można poradzić sobie
z pokryciem przypieczętowanych pól (jak?). To pozwala zredukować
złożoność czasową rozwiązania do
a żądane wartości
możemy wyznaczyć, traktując pola dozwolone jako 1, zabronione jako 0
i dwukrotnie obliczając sumy prefiksowe, najpierw w wierszach, a potem
w kolumnach kartki. Teraz sumę pól w dowolnym prostokącie wyraża się
jako sumę i różnicę co najwyżej czterech wartości dla prostokątów
prefiksowych. W ten sposób sprawdzenie poprawności przyłożenia pieczątki
można zrealizować w czasie stałym. Podobnie można poradzić sobie
z pokryciem przypieczętowanych pól (jak?). To pozwala zredukować
złożoność czasową rozwiązania do
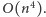
Poczynimy teraz jedno proste spostrzeżenie dotyczące monotoniczności
pieczątek. Otóż jeżeli kartkę można pokryć pieczątką
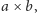 to można
ją też pokryć dowolną pieczątką
to można
ją też pokryć dowolną pieczątką
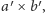 gdzie
gdzie
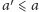 oraz
oraz
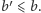 Dla każdego
Dla każdego
 możemy więc za pomocą wyszukiwania
binarnego wyznaczyć maksymalne
możemy więc za pomocą wyszukiwania
binarnego wyznaczyć maksymalne
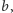 takie że pieczątką
takie że pieczątką
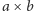 da się
pokryć całą kartkę. W ten sposób otrzymujemy rozwiązanie o złożoności
da się
pokryć całą kartkę. W ten sposób otrzymujemy rozwiązanie o złożoności
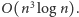 Jeśli zamiast wyszukiwania binarnego wykonamy nieco
bardziej finezyjne przeglądanie zbioru pieczątek, tzn. wraz z rosnącymi
wartościami
Jeśli zamiast wyszukiwania binarnego wykonamy nieco
bardziej finezyjne przeglądanie zbioru pieczątek, tzn. wraz z rosnącymi
wartościami
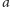 będziemy rozważać coraz mniejsze wartości
będziemy rozważać coraz mniejsze wartości
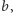 możemy obniżyć złożoność czasową rozwiązania do
możemy obniżyć złożoność czasową rozwiązania do
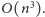
Istnieje jednak rozwiązanie działające w czasie liniowym względem rozmiaru
planszy, czyli w czasie
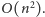 Kluczem do otrzymania takiego
rozwiązania jest przyjrzenie się polom „brzegowym”, czyli polom dozwolonym
sąsiadującym z jakimś polem zabronionym. Oczywiście, każde takie
pole musi zostać pokryte pieczątką. Chcielibyśmy w zwarty sposób
opisać zbiór wszystkich rozmiarów pieczątek, którymi można to
zrobić.
Kluczem do otrzymania takiego
rozwiązania jest przyjrzenie się polom „brzegowym”, czyli polom dozwolonym
sąsiadującym z jakimś polem zabronionym. Oczywiście, każde takie
pole musi zostać pokryte pieczątką. Chcielibyśmy w zwarty sposób
opisać zbiór wszystkich rozmiarów pieczątek, którymi można to
zrobić.
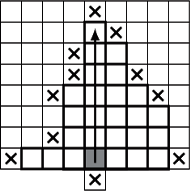
Spójrzmy na rysunek obok, na którym zamalowano jedno z pól brzegowych. Do pokrycia tego pola można użyć dowolnej pieczątki o wysokości 1 i szerokości co najwyżej 7, podobnie – dowolnej pieczątki o wysokości 2 i szerokości co najwyżej 5, dowolnej pieczątki o wysokości 3 i szerokości co najwyżej 5 itd.
Inaczej można na to spojrzeć tak: mamy pewien zbiór złych pieczątek –
w powyższym przykładzie są to
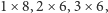
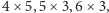
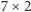 i
i
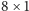 – i szukamy pieczątki, która nie zawiera żadnej złej
pieczątki (jako podprostokąta). Podobnie możemy wyznaczyć złe pieczątki dla
każdego innego pola brzegowego, pamiętając, że pole brzegowe może
sąsiadować z odpowiadającym mu polem zabronionym w jednym z czterech
kierunków. Pieczątka, której szukamy, będzie pieczątką o maksymalnym polu
niezawierającą żadnej złej pieczątki.
– i szukamy pieczątki, która nie zawiera żadnej złej
pieczątki (jako podprostokąta). Podobnie możemy wyznaczyć złe pieczątki dla
każdego innego pola brzegowego, pamiętając, że pole brzegowe może
sąsiadować z odpowiadającym mu polem zabronionym w jednym z czterech
kierunków. Pieczątka, której szukamy, będzie pieczątką o maksymalnym polu
niezawierającą żadnej złej pieczątki.
Zajmijmy się teraz implementacją algorytmu. Przede wszystkim dla każdego
dozwolonego pola planszy będziemy pamiętać odległość do najbliższego
pola zabronionego w każdym z czterech kierunków. To pozwoli nam
wyznaczać kolejne złe pieczątki o coraz większych wysokościach w czasie
stałym. Dalej, na zbiorze rozmiarów złych pieczątek zbudujemy dwuwymiarowe
sumy prefiksowe, co pozwoli nam łatwo określać, jakie pieczątki nie zawierają
w sobie żadnej z nich. Wszystkie wymienione operacje można bez problemu
wykonać w czasie
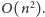 Złożoność rozwiązania zależy
jeszcze od liczby wyznaczonych złych pieczątek. Liczba ta jest równa
sumie długości odcinków przebytych przez nasz algorytm (strzałka na
rysunku). Jednak każde pole dozwolone znajduje się na dokładnie czterech
takich odcinkach, po jednym w każdym kierunku. Stąd suma długości
odcinków to co najwyżej
Złożoność rozwiązania zależy
jeszcze od liczby wyznaczonych złych pieczątek. Liczba ta jest równa
sumie długości odcinków przebytych przez nasz algorytm (strzałka na
rysunku). Jednak każde pole dozwolone znajduje się na dokładnie czterech
takich odcinkach, po jednym w każdym kierunku. Stąd suma długości
odcinków to co najwyżej
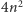 i całe rozwiązanie ma złożoność
i całe rozwiązanie ma złożoność
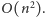
Wiemy, że wynikową pieczątką można pokryć wszystkie pola brzegowe. Należałoby jeszcze wykazać, że tak skonstruowaną pieczątką można pokryć także pozostałe pola dozwolone. Dowód tego faktu pozostawiamy do przemyślenia Czytelnikom.
Można także obejrzeć film z omówieniem: