Informatyczny kącik olimpijski
Dwa torty
W tym kąciku omówimy Dwa torty – kolejne zadanie z finałowej rundy Potyczek Algorytmicznych 2012.
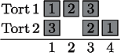
Rys. 1 Dla
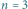 i tortów o warstwach
i tortów o warstwach
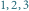 oraz
oraz
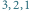 potrzebujemy
czterech minut.
potrzebujemy
czterech minut.
Zadanie. Torty oferowane przez cukiernię składają się z
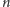 różnych
rodzajów warstw ułożonych w pewnej kolejności. Cukiernia ta zatrudnia
różnych
rodzajów warstw ułożonych w pewnej kolejności. Cukiernia ta zatrudnia
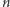 cukierników. Każdy z nich potrafi wykonać warstwę jednego
rodzaju, co zajmuje mu dokładnie jedną minutę (i w tym czasie może
zajmować się tylko jednym tortem). Warstwy na każdym torcie należy
układać jedna po drugiej. Chcemy wyprodukować dwa torty, dla każdego
z nich znamy wymaganą kolejność warstw. Należy obliczyć, jak
najszybciej da się to zrobić (Rys. 1).
cukierników. Każdy z nich potrafi wykonać warstwę jednego
rodzaju, co zajmuje mu dokładnie jedną minutę (i w tym czasie może
zajmować się tylko jednym tortem). Warstwy na każdym torcie należy
układać jedna po drugiej. Chcemy wyprodukować dwa torty, dla każdego
z nich znamy wymaganą kolejność warstw. Należy obliczyć, jak
najszybciej da się to zrobić (Rys. 1).
Dość łatwo podać rozwiązanie tego zadania oparte na programowaniu
dynamicznym i działające w czasie
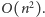 Niech
Niech
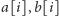 oznaczają
rodzaj
oznaczają
rodzaj
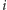 -tej warstwy od dołu (dla
-tej warstwy od dołu (dla
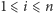 ) odpowiednio dla
pierwszego i drugiego tortu. Niech
) odpowiednio dla
pierwszego i drugiego tortu. Niech
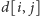 oznacza minimalny
czas ułożenia dolnych
oznacza minimalny
czas ułożenia dolnych
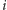 warstw na pierwszym torcie i dolnych
warstw na pierwszym torcie i dolnych
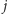 warstw na drugim torcie. Wtedy
warstw na drugim torcie. Wtedy
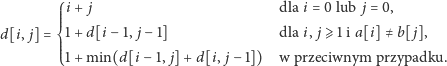 |
Zależność rekurencyjna wynika z tego, że warstwy
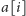 i
i
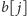 mogą
być wykonane w tym samym czasie tylko wtedy, gdy są różnego rodzaju.
W przeciwnym przypadku musimy się zdecydować, którą z nich wykonujemy
najpierw. Wynikiem jest
mogą
być wykonane w tym samym czasie tylko wtedy, gdy są różnego rodzaju.
W przeciwnym przypadku musimy się zdecydować, którą z nich wykonujemy
najpierw. Wynikiem jest
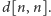
Oczywiste jest to, że wynik będzie w granicach od
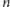 do
do
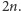 Jednak
Czytelnicy, którzy zechcą przeprowadzić kilka eksperymentów praktycznych,
przekonają się, że znalezienie przykładu z wynikiem bliskim górnej granicy nie
jest wcale łatwe. W istocie bowiem wynik nigdy nie jest większy niż
Jednak
Czytelnicy, którzy zechcą przeprowadzić kilka eksperymentów praktycznych,
przekonają się, że znalezienie przykładu z wynikiem bliskim górnej granicy nie
jest wcale łatwe. W istocie bowiem wynik nigdy nie jest większy niż
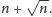 To pozwala nam przyspieszyć rozwiązanie kwadratowe do
To pozwala nam przyspieszyć rozwiązanie kwadratowe do
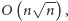 gdyż musimy jedynie wypełniać przekątne tablicy
gdyż musimy jedynie wypełniać przekątne tablicy
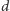 leżące nie dalej niż
leżące nie dalej niż
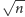 od głównej przekątnej (tzn. możemy
założyć, że
od głównej przekątnej (tzn. możemy
założyć, że
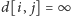 dla
dla
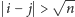 ).
).
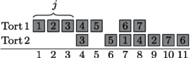
Rys. 2 Przykład dla
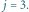 Potrzebujemy
Potrzebujemy
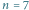 minut dla pierwszego tortu i
dodatkowo
minut dla pierwszego tortu i
dodatkowo
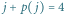 minut dla pozostałych warstw drugiego tortu.
minut dla pozostałych warstw drugiego tortu.
Musimy jeszcze wykazać, że zawsze istnieje strategia produkcji tortów,
w której wystarczy
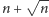 minut. Dla uproszczenia załóżmy, że
minut. Dla uproszczenia załóżmy, że
 jest kwadratem liczby naturalnej. Dla ustalonego
jest kwadratem liczby naturalnej. Dla ustalonego
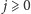 możemy
zastosować następującą strategię produkcji tortów: najpierw wykonujemy
pierwsze
możemy
zastosować następującą strategię produkcji tortów: najpierw wykonujemy
pierwsze
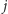 warstw pierwszego tortu, następnie
warstw pierwszego tortu, następnie
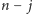 par warstw
(warstwę
par warstw
(warstwę
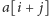 równocześnie z warstwą
równocześnie z warstwą
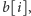 chyba że
chyba że
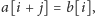 to wtedy po kolei), i w końcu ostatnie
to wtedy po kolei), i w końcu ostatnie
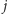 warstw
drugiego tortu (Rys. 2). Będziemy potrzebowali
warstw
drugiego tortu (Rys. 2). Będziemy potrzebowali
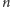 minut na wszystkie
warstwy pierwszego tortu,
minut na wszystkie
warstwy pierwszego tortu,
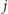 minut na ostatnie warstwy drugiego tortu
oraz
minut na ostatnie warstwy drugiego tortu
oraz
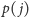 minut na te z pozostałych warstw drugiego tortu, które nie
zostały „sparowane” z warstwami pierwszego tortu. Dla
minut na te z pozostałych warstw drugiego tortu, które nie
zostały „sparowane” z warstwami pierwszego tortu. Dla
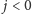 definiujemy
analogiczną strategię, tylko zaczynamy od pierwszych
definiujemy
analogiczną strategię, tylko zaczynamy od pierwszych
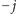 warstw drugiego
tortu.
warstw drugiego
tortu.
Kluczową obserwacją jest to, że dla ustalonego rodzaju warstwy
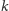 warunek
warunek
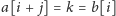 jest spełniony dla dokładnie jednego
jest spełniony dla dokładnie jednego
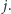 Z tego
wynika, że suma
Z tego
wynika, że suma
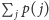 jest równa
jest równa
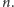 Sumując czas potrzebny
dla wszystkich strategii dla
Sumując czas potrzebny
dla wszystkich strategii dla
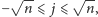 dostajemy:
dostajemy:

czyli średnio na strategię potrzebujemy nie więcej niż
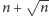 minut,
zatem istnieje takie
minut,
zatem istnieje takie
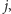 dla którego tyle wystarczy.
dla którego tyle wystarczy.
Dla pełności dodajmy, że wynik
 uzyskujemy dla tortu
uzyskujemy dla tortu
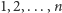 oraz tortu, w którym warstwy dzielimy na grupy kolejnych
warstw o rozmiarach
oraz tortu, w którym warstwy dzielimy na grupy kolejnych
warstw o rozmiarach
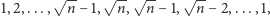 a następnie
odwracamy kolejność warstw w każdej grupie. Przykładowo, dla
a następnie
odwracamy kolejność warstw w każdej grupie. Przykładowo, dla
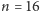 drugim tortem jest
drugim tortem jest
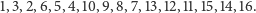 |
Powyższe rozważania stają się nieistotne, jeśli przyjrzymy się dokładniej rekurencji
definiującej tablicę
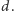 Zauważmy, że obliczenie
Zauważmy, że obliczenie
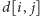 w przypadku
w przypadku
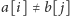 zależy tylko od jednej komórki tabeli. Zatem możemy
rozwinąć wzór do
zależy tylko od jednej komórki tabeli. Zatem możemy
rozwinąć wzór do
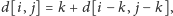 gdzie
gdzie
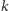 jest taką
najmniejszą liczbą, że
jest taką
najmniejszą liczbą, że
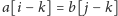 i
i
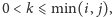 lub
lub
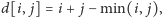 gdy takie
gdy takie
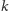 nie istnieje.
nie istnieje.
Zatem obliczenie dowolnego
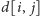 sprowadza się do wyznaczenia
wartości
sprowadza się do wyznaczenia
wartości
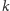 (co można zrobić w czasie
(co można zrobić w czasie
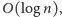 wyszukując
binarnie wśród par
wyszukując
binarnie wśród par
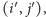 dla których
dla których
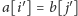 oraz
oraz
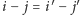 ) i obliczenia
) i obliczenia
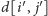 dla przypadku
dla przypadku
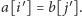 Zauważmy jednak, że mamy dokładnie
Zauważmy jednak, że mamy dokładnie
 par
par
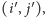 dla których
dla których
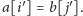 Wyznaczając więc
Wyznaczając więc
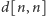 metodą rekurencji ze spamiętywaniem, dostajemy rozwiązanie
działające w czasie
metodą rekurencji ze spamiętywaniem, dostajemy rozwiązanie
działające w czasie
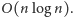 Czytelnik Gorliwy zechce uzupełnić
techniczne szczegóły, które przyspieszą powyższe rozwiązanie do optymalnego
Czytelnik Gorliwy zechce uzupełnić
techniczne szczegóły, które przyspieszą powyższe rozwiązanie do optymalnego
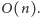
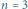 i tortów o warstwach
i tortów o warstwach
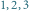 oraz
oraz
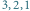 potrzebujemy
czterech minut.
potrzebujemy
czterech minut.
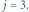 Potrzebujemy
Potrzebujemy
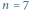 minut dla pierwszego tortu i
dodatkowo
minut dla pierwszego tortu i
dodatkowo
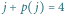 minut dla pozostałych warstw drugiego tortu.
minut dla pozostałych warstw drugiego tortu.