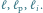Zawieramy wielokąty
Na artykule Problemy 3sum-trudne w geometrii autor podał trzy wersje problemu PolygonContainment, które są uważane za trudne – nie umiemy ich rozwiązać w czasie (istotnie) lepszym niż kwadratowy. Uważni Czytelnicy na pewno zauważyli, że nie jest tam wspomniane o wersji, w której wielokąty są wypukłe i dopuszczamy dowolne przesunięcia (ale nie obroty). Ten brak jest w pełni uzasadniony, gdyż tę wersję problemu można rozwiązać w czasie liniowym względem liczby wierzchołków wielokątów, co pokażemy poniżej.
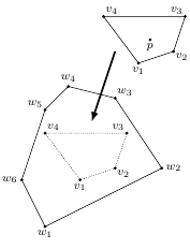
Rys. 1 Wielokąt
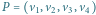 można umieścić wewnątrz wielokąta
można umieścić wewnątrz wielokąta
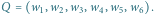
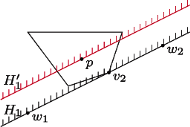
Rys. 2 Wierzchołek
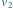 jest wierzchołkiem krytycznym dla boku
jest wierzchołkiem krytycznym dla boku
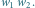
Niech
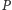 będzie wielokątem o wierzchołkach
będzie wielokątem o wierzchołkach
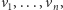 który
chcemy umieścić wewnątrz wielokąta
który
chcemy umieścić wewnątrz wielokąta
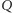 o wierzchołkach
o wierzchołkach
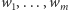 (przyjmujemy, że
(przyjmujemy, że
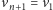 i
i
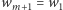 ). Niech
). Niech
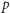 będzie dowolnym punktem wewnątrz wielokąta
będzie dowolnym punktem wewnątrz wielokąta
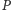 (Rys. 1).
Załóżmy dla uproszczenia, że żadna para boków wielokątów nie jest
równoległa oraz żaden bok nie jest pionowy.
(Rys. 1).
Załóżmy dla uproszczenia, że żadna para boków wielokątów nie jest
równoległa oraz żaden bok nie jest pionowy.
Przez
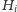 (dla
(dla
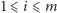 ) oznaczmy tę półpłaszczyznę wyznaczoną
przez prostą
) oznaczmy tę półpłaszczyznę wyznaczoną
przez prostą
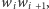 która zawiera wielokąt
która zawiera wielokąt
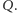 Przesuńmy teraz
wielokąt
Przesuńmy teraz
wielokąt
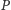 tak, aby zawierał się w
tak, aby zawierał się w
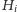 i aby odległość punktu
i aby odległość punktu
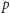 od prostej
od prostej
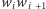 była jak najmniejsza; oznaczmy tę odległość
przez
była jak najmniejsza; oznaczmy tę odległość
przez
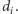 Zauważmy, że
Zauważmy, że
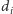 możemy obliczyć bez kłopotu,
jeśli wyznaczymy wierzchołek przesuniętego wielokąta
możemy obliczyć bez kłopotu,
jeśli wyznaczymy wierzchołek przesuniętego wielokąta
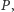 który leży
na brzegu półpłaszczyzny
który leży
na brzegu półpłaszczyzny
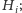 nazwiemy ten wierzchołek krytycznym dla
boku
nazwiemy ten wierzchołek krytycznym dla
boku
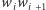 (Rys. 2).
(Rys. 2).
Zauważmy, że wielokąt
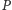 zawiera się w
zawiera się w
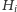 dokładnie wtedy, gdy
punkt
dokładnie wtedy, gdy
punkt
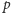 zawiera się w półpłaszczyźnie
zawiera się w półpłaszczyźnie
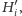 która jest
wyznaczona przez prostą równoległą do
która jest
wyznaczona przez prostą równoległą do
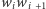 w odległości
w odległości
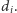 Jest jasne, że
Jest jasne, że
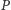 znajduje się wewnątrz
znajduje się wewnątrz
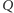 dokładnie
wtedy, gdy znajduje się w każdej z półpłaszczyzn
dokładnie
wtedy, gdy znajduje się w każdej z półpłaszczyzn
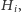 innymi słowy
wtedy, gdy punkt
innymi słowy
wtedy, gdy punkt
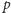 należy do przecięcia półpłaszczyzn
należy do przecięcia półpłaszczyzn
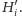 Co
więcej, przecięcie półpłaszczyzn zawiera wszystkie możliwe położenia punktu
Co
więcej, przecięcie półpłaszczyzn zawiera wszystkie możliwe położenia punktu
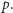
Do pełnego rozwiązania pozostaje zatem pokazanie, jak efektywnie wyznaczyć wierzchołki krytyczne, a następnie przecięcie półpłaszczyzn.
Wyznaczanie wierzchołków krytycznych
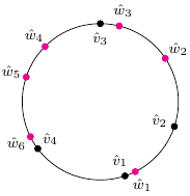
Rys. 3 Nachylenia boków wielokątów naniesione na okrąg.
Narysujmy okrąg i zaznaczmy na nim, dla
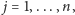 punkt
styczności
punkt
styczności
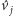 prostej stycznej do okręgu i równoległej do prostej
prostej stycznej do okręgu i równoległej do prostej
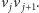 Analogicznie zaznaczamy punkt
Analogicznie zaznaczamy punkt
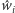 dla prostej
dla prostej
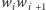 (Rys. 3). Zauważmy, że wierzchołek
(Rys. 3). Zauważmy, że wierzchołek
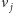 jest krytyczny dla boku
jest krytyczny dla boku
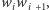 jeśli na okręgu punkt
jeśli na okręgu punkt
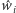 leży pomiędzy punktami
leży pomiędzy punktami
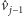 oraz
oraz
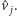 Wystarczy zatem wyznaczyć kolejność punktów
na okręgu – to można zrobić w czasie
Wystarczy zatem wyznaczyć kolejność punktów
na okręgu – to można zrobić w czasie
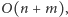 gdyż należy scalić
dwa posortowane ciągi punktów (zakładamy przy tym, że znamy kolejność
wierzchołków na obwodach wielokątów).
gdyż należy scalić
dwa posortowane ciągi punktów (zakładamy przy tym, że znamy kolejność
wierzchołków na obwodach wielokątów).
Na ten problem można spojrzeć też inaczej. Wyobraźmy sobie dwie proste
równoległe, które jednocześnie obracają się wokół wielokątów, będąc do
nich stycznymi. Ilekroć prosta styczna do
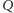 zawiera pewien jego bok, to
prosta styczna do
zawiera pewien jego bok, to
prosta styczna do
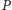 przechodzi przez wierzchołek krytyczny dla tego
boku.
przechodzi przez wierzchołek krytyczny dla tego
boku.
Pozostawiamy Czytelnikowi zaimplementowanie tego pomysłu, tak by działał
w czasie
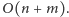 Metoda prostych równoległych pozwala rozwiązać
wiele problemów dotyczących wielokątów wypukłych – zainteresowani
Czytelnicy więcej szczegółów mogą znaleźć w Internecie pod hasłem
rotating calipers.
Metoda prostych równoległych pozwala rozwiązać
wiele problemów dotyczących wielokątów wypukłych – zainteresowani
Czytelnicy więcej szczegółów mogą znaleźć w Internecie pod hasłem
rotating calipers.
Wyznaczanie przecięcia półpłaszczyzn
W ogólności problem ten dla
 półpłaszczyzn wymaga czasu
półpłaszczyzn wymaga czasu
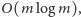 ale my znowu skorzystamy z tego, że znamy kolejność
wierzchołków w wielokącie
ale my znowu skorzystamy z tego, że znamy kolejność
wierzchołków w wielokącie
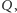 zatem nasze półpłaszczyzny
zatem nasze półpłaszczyzny
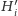 są posortowane według współczynników kierunkowych ich
brzegów (prostych
są posortowane według współczynników kierunkowych ich
brzegów (prostych
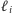 ), co pozwala nam rozwiązać ten problem w czasie
), co pozwala nam rozwiązać ten problem w czasie
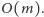
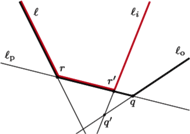
Rys. 4 Rozpatrujemy prostą
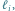 na stosie znajdują się proste
na stosie znajdują się proste
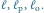 Punkt
Punkt
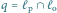 znajduje się na prawo od punktu
znajduje się na prawo od punktu
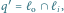 zatem usuwamy ze stosu
prostą
zatem usuwamy ze stosu
prostą
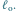 Punkt
Punkt
 jest na lewo od
jest na lewo od
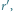 zatem na stosie pozostaną proste
zatem na stosie pozostaną proste
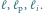
Najpierw pokażemy, jak wyznaczyć „dolne” przecięcie, tzn. dla półpłaszczyzn,
które mogą stanowić dolny brzeg wielokąta będącego przecięciem.
Przeglądamy półpłaszczyzny w kolejności rosnących współczynników
kierunkowych prostych
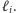 Będziemy utrzymywać następujący
niezmiennik: po rozpatrzeniu prostej
Będziemy utrzymywać następujący
niezmiennik: po rozpatrzeniu prostej
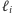 na stosie znajdują się te proste
z ciągu
na stosie znajdują się te proste
z ciągu
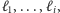 które mają nietrywialne przecięcie z brzegiem zbioru
które mają nietrywialne przecięcie z brzegiem zbioru
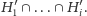
Rozpatrując
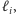 robimy co następuje: dopóki punkt przecięcia prostych
robimy co następuje: dopóki punkt przecięcia prostych
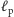 i
i
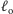 (przedostatniej i ostatniej prostej na stosie) znajduje się na
prawo od punktu przecięcia prostych
(przedostatniej i ostatniej prostej na stosie) znajduje się na
prawo od punktu przecięcia prostych
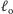 i
i
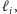 usuwamy
ostatnią prostą ze stosu. Na końcu dodajemy prostą
usuwamy
ostatnią prostą ze stosu. Na końcu dodajemy prostą
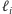 na stos (patrz
Rys. 4).
na stos (patrz
Rys. 4).
Analogicznie wyznaczamy przecięcie „górnych” półpłaszczyzn. Obliczenie
przecięcia powstałych zbiorów w czasie
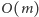 pozostawimy jako
ćwiczenie dla Czytelnika.
pozostawimy jako
ćwiczenie dla Czytelnika.
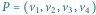 można umieścić wewnątrz wielokąta
można umieścić wewnątrz wielokąta
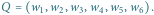
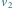 jest wierzchołkiem krytycznym dla boku
jest wierzchołkiem krytycznym dla boku
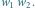
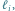 na stosie znajdują się proste
na stosie znajdują się proste
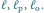 Punkt
Punkt
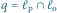 znajduje się na prawo od punktu
znajduje się na prawo od punktu
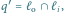 zatem usuwamy ze stosu
prostą
zatem usuwamy ze stosu
prostą
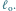 Punkt
Punkt
 jest na lewo od
jest na lewo od
 zatem na stosie pozostaną proste
zatem na stosie pozostaną proste