Złośliwy problem (MAX , +) i kubełkowe struktury danych

Dany jest ciąg złożony z
 nieujemnych liczb całkowitych
nieujemnych liczb całkowitych
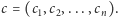 Na ciągu
Na ciągu
 chcemy wykonywać operacje
dwóch rodzajów:
chcemy wykonywać operacje
dwóch rodzajów:
- update
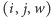 – modyfikuje wartości wyrazów
ciągu o indeksach z przedziału od
– modyfikuje wartości wyrazów
ciągu o indeksach z przedziału od
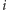 do
do
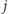 w sposób
zależny od parametru
w sposób
zależny od parametru
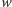 (dodatniej liczby całkowitej);
(dodatniej liczby całkowitej);
- query
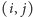 – podaje zagregowaną wartość dla podciągu
o indeksach od
– podaje zagregowaną wartość dla podciągu
o indeksach od
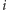 do
do
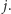
W obydwu przypadkach zakładamy, że
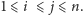
Będziemy rozważali dwie różne operacje update, które oznaczymy symbolicznie
przez
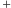 i
i
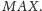 W operacji
W operacji
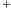 należy do każdego
wyrazu podciągu
należy do każdego
wyrazu podciągu
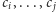 dodać liczbę
dodać liczbę
 Z kolei operacja
Z kolei operacja
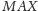 polega na zmianie wartości wyrazu
polega na zmianie wartości wyrazu
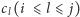 na
na
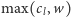 – innymi słowy, jeśli wyraz miał wcześniej wartość nie
mniejszą niż
– innymi słowy, jeśli wyraz miał wcześniej wartość nie
mniejszą niż
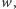 to jej nie zmienia, a jeśli jego wartość była mniejsza
od
to jej nie zmienia, a jeśli jego wartość była mniejsza
od
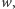 to jego nową wartością jest
to jego nową wartością jest
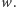
Podobnie definiujemy dwie operacje query:
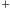 i
i
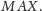 Na
zapytanie
Na
zapytanie
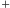 odpowiadamy, podając sumę wyrazów z podciągu
odpowiadamy, podając sumę wyrazów z podciągu
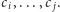 Odpowiedzią na zapytanie typu
Odpowiedzią na zapytanie typu
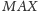 jest natomiast
wartość największego wyrazu w rozważanym podciągu.
jest natomiast
wartość największego wyrazu w rozważanym podciągu.
Biorąc pod uwagę wszystkie kombinacje poszczególnych operacji,
otrzymujemy cztery różne warianty problemu. Każdy taki wariant
oznaczamy za pomocą pary, której pierwszy wyraz opisuje rodzaj operacji
modyfikacji, a drugi określa zapytanie. Mamy zatem następujące warianty:
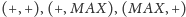 oraz
oraz
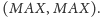
Okazuje się, że nasz problem ma kilka ciekawych zastosowań. Wariant
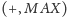 można wykorzystać do implementacji systemu obsługi
rezerwacji miejsc w pociągu na trasie łączącej
można wykorzystać do implementacji systemu obsługi
rezerwacji miejsc w pociągu na trasie łączącej
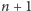 stacji. W pociągu
znajduje się ustalona liczba miejsc siedzących. Każda rezerwacja dotyczy
konkretnej liczby pasażerów i wskazuje numery dwóch stacji, na
których pasażerowie zamierzają wsiąść i wysiąść. Naszym celem jest
przyjmować kolejno wszystkie rezerwacje, które nie powodują przepełnienia
pociągu.
stacji. W pociągu
znajduje się ustalona liczba miejsc siedzących. Każda rezerwacja dotyczy
konkretnej liczby pasażerów i wskazuje numery dwóch stacji, na
których pasażerowie zamierzają wsiąść i wysiąść. Naszym celem jest
przyjmować kolejno wszystkie rezerwacje, które nie powodują przepełnienia
pociągu.
Oznaczmy przez
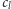 aktualną liczbę pasażerów, którzy będą w pociągu
na trasie pomiędzy stacjami
aktualną liczbę pasażerów, którzy będą w pociągu
na trasie pomiędzy stacjami
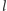 oraz
oraz
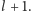 Rezerwację na podróż
ze stacji
Rezerwację na podróż
ze stacji
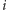 do stacji
do stacji
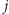 dla
dla
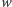 pasażerów możemy
przyjąć, jeśli wartość query
pasażerów możemy
przyjąć, jeśli wartość query
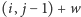 jest nie większa niż
liczba miejsc w pociągu. Po przyjęciu rezerwacji wykonujemy update
jest nie większa niż
liczba miejsc w pociągu. Po przyjęciu rezerwacji wykonujemy update
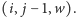
Inaczej można na to spojrzeć jak na problem kontroli przesyłania danych między serwerami połączonymi jedną linią danych o określonej przepustowości albo problem obsługi pobierania danych z Internetu przez użytkowników sieci lokalnej w zadanych przedziałach czasowych (sieć ma ograniczony transfer).
Wariant
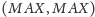 ma natomiast elegancką interpretację
kombinatoryczną powiązaną z popularną grą Tetris. Odpowiada on mianowicie
sytuacji, w której klocki, które opadają na planszę, mają regularną strukturę
(np. mają kształt prostokątów), a naszym celem jest, dla każdego klocka, orzec,
w którym miejscu się on zatrzyma, jeśli spuścimy go z zadanej pozycji
początkowej (nie mamy możliwości wykonywania w locie obrotów ani
przesunięć). Z kolei wariant
ma natomiast elegancką interpretację
kombinatoryczną powiązaną z popularną grą Tetris. Odpowiada on mianowicie
sytuacji, w której klocki, które opadają na planszę, mają regularną strukturę
(np. mają kształt prostokątów), a naszym celem jest, dla każdego klocka, orzec,
w którym miejscu się on zatrzyma, jeśli spuścimy go z zadanej pozycji
początkowej (nie mamy możliwości wykonywania w locie obrotów ani
przesunięć). Z kolei wariant
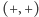 reprezentuje dynamiczny problem
obliczania sum częściowych ciągu.
reprezentuje dynamiczny problem
obliczania sum częściowych ciągu.
Trzy z podanych wariantów wyjściowego problemu mają zatem jasno
określoną interpretację. Co więcej, znane są ich efektywne rozwiązania,
w których koszt obsługi ciągu
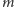 zapytań to
zapytań to
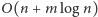 (szukaną strukturą danych są tzw. drzewa przedziałowe, o których więcej
można przeczytać lub posłuchać na stronie http://was.zaa.mimuw.edu.pl).
(szukaną strukturą danych są tzw. drzewa przedziałowe, o których więcej
można przeczytać lub posłuchać na stronie http://was.zaa.mimuw.edu.pl).
Za to czwarty wariant,
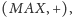 jest inny. Jego interpretacja
kombinatoryczna nie jest wcale aż tak jasna, a do tego nie znamy sposobu
rozwiązania go w czasie
jest inny. Jego interpretacja
kombinatoryczna nie jest wcale aż tak jasna, a do tego nie znamy sposobu
rozwiązania go w czasie
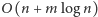 (w tym przypadku klasyczne
drzewa przedziałowe nie sprawdzają się). Okazuje się jednak, że można go
w miarę prosto rozwiązać, korzystając z pewnej kubełkowej struktury danych.
Nasze rozwiązanie będzie działało w czasie
(w tym przypadku klasyczne
drzewa przedziałowe nie sprawdzają się). Okazuje się jednak, że można go
w miarę prosto rozwiązać, korzystając z pewnej kubełkowej struktury danych.
Nasze rozwiązanie będzie działało w czasie
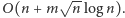
Zacznijmy od podziału wyrazów ciągu pomiędzy kubełki, umieszczając
w każdym kubełku, z wyjątkiem ostatniego,
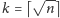 wyrazów.
Jeśli ostatni kubełek jest mniejszy, możemy uzupełnić go sztucznymi
wyrazami do rozmiaru
wyrazów.
Jeśli ostatni kubełek jest mniejszy, możemy uzupełnić go sztucznymi
wyrazami do rozmiaru
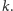 Oprócz kolejnych wyrazów ciągu kubełek
będzie przechowywał pewne dane pomocnicze. Zanim opiszemy strukturę
kubełka, zaproponujmy trochę inny sposób myślenia o operacji update
Oprócz kolejnych wyrazów ciągu kubełek
będzie przechowywał pewne dane pomocnicze. Zanim opiszemy strukturę
kubełka, zaproponujmy trochę inny sposób myślenia o operacji update
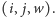 Zamiast mówić, że dla każdego
Zamiast mówić, że dla każdego
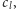 takiego że
takiego że
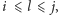 wykonujemy
wykonujemy
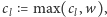 można wyobrazić
sobie, że dodajemy nowe ograniczenie dolne na liczby na pozycjach od
można wyobrazić
sobie, że dodajemy nowe ograniczenie dolne na liczby na pozycjach od
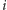 do
do
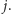 Wtedy wartość liczby w kubełku będzie równa
maksimum z jej początkowej wartości oraz wszystkich ograniczeń dolnych jej
dotyczących. Takie ograniczenia dolne będą trzymane osobno dla każdego
kubełka.
Wtedy wartość liczby w kubełku będzie równa
maksimum z jej początkowej wartości oraz wszystkich ograniczeń dolnych jej
dotyczących. Takie ograniczenia dolne będą trzymane osobno dla każdego
kubełka.
Struktura kubełka będzie następująca:
-
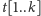 – tablica kolejnych wyrazów ciągu, które znajdują
się w kubełku;
– tablica kolejnych wyrazów ciągu, które znajdują
się w kubełku;
-
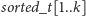 – posortowana tablica liczb
– posortowana tablica liczb
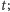
-
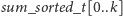 – sumy prefiksowe tablicy
– sumy prefiksowe tablicy
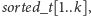 czyli
czyli
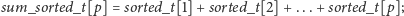
-
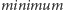 – dolne ograniczenie na wszystkie wyrazy ciągu
przechowywane w kubełku, czyli maksimum z wartości
– dolne ograniczenie na wszystkie wyrazy ciągu
przechowywane w kubełku, czyli maksimum z wartości
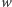 z operacji update
z operacji update
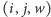 dotyczących
całego przedziału kubełka; aktualna wartość
dotyczących
całego przedziału kubełka; aktualna wartość
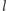 -tej liczby
z kubełka to zawsze
-tej liczby
z kubełka to zawsze
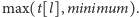
Każdy kubełek umożliwia wykonywanie następujących operacji pomocniczych (szczegółowy opis ich implementacji znajduje się w dalszej części artykułu):
- 1.
-
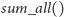 – obliczenie sumy aktualnych wartości wszystkich
wyrazów ciągu zawartych w kubełku (działa w czasie
– obliczenie sumy aktualnych wartości wszystkich
wyrazów ciągu zawartych w kubełku (działa w czasie
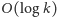 );
);
- 2.
-
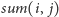 – obliczenie sumy wyrazów o indeksach od
– obliczenie sumy wyrazów o indeksach od
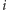 do
do
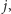 dla
dla
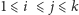 (działa w czasie
(działa w czasie
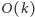 );
);
- 3.
-
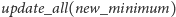 – aktualizacja dolnego ograniczenia na
całym przedziale do wartości co najmniej
– aktualizacja dolnego ograniczenia na
całym przedziale do wartości co najmniej
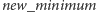 (działa
w czasie
(działa
w czasie
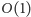 );
);
- 4.
-
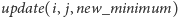 – zwiększenie wyrazów o indeksach
od
– zwiększenie wyrazów o indeksach
od
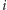 do
do
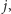 dla
dla
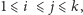 do wartości co
najmniej
do wartości co
najmniej
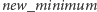 (działa w czasie
(działa w czasie
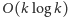 ).
).
Zauważmy teraz, że dowolny zakres indeksów od
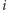 do
do
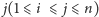 można rozbić na pewną liczbę pełnych kubełków
(oczywiście, nie więcej niż
można rozbić na pewną liczbę pełnych kubełków
(oczywiście, nie więcej niż
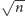 ) oraz na co najwyżej dwa niepełne
kubełki (te skrajne). Dzięki temu zapytanie o sumę liczb na przedziale od
) oraz na co najwyżej dwa niepełne
kubełki (te skrajne). Dzięki temu zapytanie o sumę liczb na przedziale od
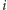 do
do
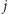 można podzielić na nie więcej niż
można podzielić na nie więcej niż
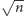 zapytań
zapytań
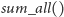 oraz co najwyżej dwa zapytania
oraz co najwyżej dwa zapytania
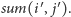 Stąd
każde takie zapytanie obsługujemy w czasie
Stąd
każde takie zapytanie obsługujemy w czasie
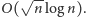 Operację
modyfikacji ciągu na indeksach od
Operację
modyfikacji ciągu na indeksach od
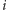 do
do
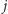 można także
wykonać w czasie
można także
wykonać w czasie
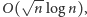 podobnie rozbijając cały przedział na
nie więcej niż
podobnie rozbijając cały przedział na
nie więcej niż
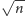 kubełków, na których wykonujemy operację
kubełków, na których wykonujemy operację
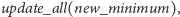 i co najwyżej dwa brzegowe kubełki
z wykonywaną operacją
i co najwyżej dwa brzegowe kubełki
z wykonywaną operacją
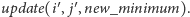
Przykład 1.
W tabeli przedstawiono, jak zmienia się przykładowa kubełkowa struktura
danych
 w wyniku pojedynczej modyfikacji. Warto zwrócić
uwagę, że w środkowym kubełku zmienia się tylko dolne ograniczenie, tj.
w wyniku pojedynczej modyfikacji. Warto zwrócić
uwagę, że w środkowym kubełku zmienia się tylko dolne ograniczenie, tj.
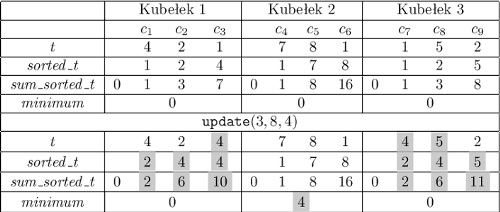
Pozostaje opisać, jak korzystając z przechowywanych danych, efektywnie wykonać cztery operacje pomocnicze oferowane przez kubełek.

Ostatnią pozycję
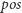 znajdujemy, wyszukując binarnie. Zauważmy,
że w tablicy
znajdujemy, wyszukując binarnie. Zauważmy,
że w tablicy
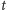 jest dokładnie
jest dokładnie
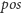 liczb mniejszych od
liczb mniejszych od
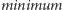 oraz dokładnie
oraz dokładnie
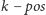 liczb nie mniejszych
niż
liczb nie mniejszych
niż
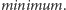 Skoro aktualna wartość każdej liczby to
Skoro aktualna wartość każdej liczby to
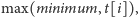 więc suma aktualnych wartości wynosi
więc suma aktualnych wartości wynosi
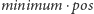 (sumujemy
(sumujemy
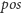 najmniejszych liczb) plus suma
najmniejszych liczb) plus suma
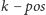 największych liczb, czyli
największych liczb, czyli
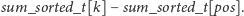

W powyższej funkcji sumujemy aktualne wartości wyrazów z kubełka z określonych pozycji.
Aktualizacja dolnego ograniczenia na cały kubełek jest bardzo łatwa:

Jeśli pojawia się nowe dolne ograniczenie, które nie dotyczy całego
zakresu obejmowanego przez kubełek, lecz jedynie jego części, należy
zaktualizować liczby tylko z tego zakresu. Niestety, po takiej operacji tablice
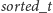 oraz
oraz
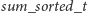 stają się nieaktualne, więc obliczamy je
ponownie. Oto zapis stosownego algorytmu:
stają się nieaktualne, więc obliczamy je
ponownie. Oto zapis stosownego algorytmu:

Zaprezentowane rozwiązanie jest dosyć szybkie, jednak nie widać powodu, dla
którego problemu
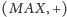 nie można by rozwiązać jeszcze szybciej.
Być może któremuś z Czytelników uda się skonstruować takie
rozwiązanie?
nie można by rozwiązać jeszcze szybciej.
Być może któremuś z Czytelników uda się skonstruować takie
rozwiązanie?
Czytelnik, który do końca lipca 2013 roku przyśle do redakcji rozwiązanie
opisanego problemu o najlepszej złożoności, nie gorszej jednak niż
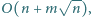 zostanie nagrodzony kilogramem szwajcarskiej czekolady
w przesyłce prosto z Zurychu. W przypadku wielu rozwiązań o tej samej
złożoności nagrodzimy subiektywnie najładniejsze, w przypadku tego samego
najładniejszego rozwiązania – pierwsze spośród otrzymanych.
zostanie nagrodzony kilogramem szwajcarskiej czekolady
w przesyłce prosto z Zurychu. W przypadku wielu rozwiązań o tej samej
złożoności nagrodzimy subiektywnie najładniejsze, w przypadku tego samego
najładniejszego rozwiązania – pierwsze spośród otrzymanych.