Największy wspólny dzielnik
Podobnie jak wyznaczanie liczb pierwszych, problem znajdowania największego
wspólnego dzielnika (NWD) dwóch liczb naturalnych ma klasyczne i zapewne
wszystkim Czytelnikom znane rozwiązanie. Mowa oczywiście o algorytmie
Euklidesa, jednym z najstarszych do dziś używanych algorytmów. Jest to
rozwiązanie bardzo proste w implementacji, a w wersji z dzieleniem –
efektywne: pozwala wyznaczyć NWD dwóch liczb nie większych niż
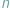 w czasie
w czasie
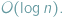 W pewnych przypadkach istnieją jednak
rozwiązania asymptotycznie szybsze.
W pewnych przypadkach istnieją jednak
rozwiązania asymptotycznie szybsze.
Załóżmy, że chcemy wyznaczać największy wspólny dzielnik dla wielu
par stosunkowo niewielkich liczb. A konkretnie – dla
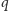 par liczb
całkowitych dodatnich nieprzekraczających
par liczb
całkowitych dodatnich nieprzekraczających
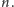 Stosując algorytm
Euklidesa, otrzymujemy oczywiście algorytm o złożoności czasowej
Stosując algorytm
Euklidesa, otrzymujemy oczywiście algorytm o złożoności czasowej
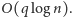 Możemy także spamiętać w dużej tablicy odpowiedzi na
wszystkie możliwe
Możemy także spamiętać w dużej tablicy odpowiedzi na
wszystkie możliwe
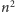 zapytań. Wówczas przy pierwszym podejściu
możemy otrzymać złożoność
zapytań. Wówczas przy pierwszym podejściu
możemy otrzymać złożoność
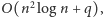 gdy dla każdej
możliwej pary zastosujemy niezależnie algorytm Euklidesa. Bez problemów
takie rozwiązanie możemy przyspieszyć do
gdy dla każdej
możliwej pary zastosujemy niezależnie algorytm Euklidesa. Bez problemów
takie rozwiązanie możemy przyspieszyć do
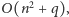 ponieważ
pojedynczy krok algorytmu Euklidesa sprowadza wyznaczanie NWD
dla pary
ponieważ
pojedynczy krok algorytmu Euklidesa sprowadza wyznaczanie NWD
dla pary
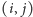 do problemu obliczenia NWD dla pewnej pary
leksykograficznie mniejszej. Możemy zatem wypełniać tablicę w odpowiedniej
kolejności i w każdym kroku przepisywać wynik ze wskazanej komórki.
W praktyce lepiej w tej sytuacji korzystać z algorytmu Euklidesa w wersji
z odejmowaniem, gdyż procesory wykonują je istotnie szybciej niż
wyznaczanie reszty z dzielenia. Otrzymujemy w ten sposób następujący
algorytm:
do problemu obliczenia NWD dla pewnej pary
leksykograficznie mniejszej. Możemy zatem wypełniać tablicę w odpowiedniej
kolejności i w każdym kroku przepisywać wynik ze wskazanej komórki.
W praktyce lepiej w tej sytuacji korzystać z algorytmu Euklidesa w wersji
z odejmowaniem, gdyż procesory wykonują je istotnie szybciej niż
wyznaczanie reszty z dzielenia. Otrzymujemy w ten sposób następujący
algorytm:
![Algorytm tablicuj-nwd(n)
for i = 1to n do
nwd[i,i] = i;
for i = 1to n do
for j = 1toi −1 do
nwd[j , i] = nwd[i, j] = nwd[ j,i − j];](/math/temat/informatyka/algorytmy/2012/12/28/Najwiekszy_wspolny_dzielnik/8x-ceb1c4ced47a0d2425b62b0d880e7420c42d7723-dm-33,33,33-FF,FF,FF.gif)
 jest jednak mało satysfakcjonujący
– dopiero przy
jest jednak mało satysfakcjonujący
– dopiero przy
 zapytaniach podejście korzystające
z algorytmu Euklidesa przestaje osiągać lepsze wyniki.
zapytaniach podejście korzystające
z algorytmu Euklidesa przestaje osiągać lepsze wyniki.Spróbujmy odnieść pewne korzyści już z obliczeń wstępnych rzędu
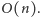 Jak przekonaliśmy się w poprzednim artykule, w tym
czasie można wyznaczyć wszystkie liczby pierwsze nieprzekraczające
Jak przekonaliśmy się w poprzednim artykule, w tym
czasie można wyznaczyć wszystkie liczby pierwsze nieprzekraczające
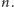 Zaprezentowany tam algorytm jest jednak znacznie silniejszy – dla każdej
liczby
Zaprezentowany tam algorytm jest jednak znacznie silniejszy – dla każdej
liczby
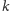 oblicza jej najmniejszy dzielnik pierwszy (oznaczany tu przez
oblicza jej najmniejszy dzielnik pierwszy (oznaczany tu przez
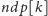 ) oraz największą potęgę tego
) oraz największą potęgę tego
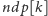 dzielącą
dzielącą
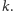 Za ich
pomocą można łatwo skonstruować algorytm znajdowania NWD, działający
w czasie proporcjonalnym do liczby różnych dzielników pierwszych
argumentów. Pesymistycznie wielkość ta wynosi
Za ich
pomocą można łatwo skonstruować algorytm znajdowania NWD, działający
w czasie proporcjonalnym do liczby różnych dzielników pierwszych
argumentów. Pesymistycznie wielkość ta wynosi
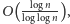 więc
zapytania obsługiwane są niewiele szybciej niż przez algorytm Euklidesa.
Okazuje się jednak, że przy liniowych obliczeniach wstępnych można
osiągnąć stały czas zapytania!
więc
zapytania obsługiwane są niewiele szybciej niż przez algorytm Euklidesa.
Okazuje się jednak, że przy liniowych obliczeniach wstępnych można
osiągnąć stały czas zapytania!
Na wstępie zauważmy, że jeśli jeden z argumentów jest liczbą pierwszą,
obliczenie NWD jest bardzo łatwe. Również łatwo możemy wyznaczać
NWD liczb mniejszych niż
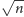 : jeśli mamy do dyspozycji czas
: jeśli mamy do dyspozycji czas
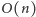 na obliczenia wstępne, można spamiętać wszystkie wartości
NWD, wywołując
na obliczenia wstępne, można spamiętać wszystkie wartości
NWD, wywołując
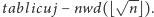 Jak się wkrótce przekonamy,
dowolne zapytanie o NWD można sprowadzić do stałej liczby zapytań,
w których każdy z argumentów jest liczbą pierwszą lub nie przekracza
Jak się wkrótce przekonamy,
dowolne zapytanie o NWD można sprowadzić do stałej liczby zapytań,
w których każdy z argumentów jest liczbą pierwszą lub nie przekracza
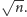 Kluczowe jest tu pojęcie rozkładu specjalnego.
Kluczowe jest tu pojęcie rozkładu specjalnego.
Definicja. Rozkładem specjalnym dodatniej liczby całkowitej
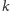 nazwiemy trójkę liczb całkowitych
nazwiemy trójkę liczb całkowitych
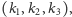 dla której
dla której
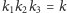 oraz dla każdego
oraz dla każdego
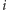 :
:

Przykładowo, jednym z rozkładów specjalnych liczby
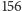 jest
jest
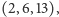 liczby
liczby
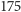 jest
jest
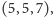 a liczby
a liczby
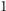 jest
jest
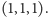
Następujący lemat stanowi podstawę indukcyjnego dowodu faktu, że każda
dodatnia liczba całkowita ma rozkład specjalny. Ten dowód można natychmiast
przekształcić w algorytm wyznaczający rozkłady specjalne wszystkich
liczb od
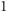 do
do
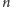 w czasie liniowym na podstawie tablicy
w czasie liniowym na podstawie tablicy
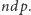
Lemat. Niech
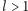 będzie liczbą całkowitą,
będzie liczbą całkowitą,
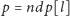 oraz
oraz
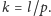 Niech
Niech
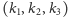 będzie
rozkładem specjalnym
będzie
rozkładem specjalnym
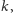 dla którego
dla którego
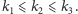 Wówczas
Wówczas
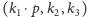 jest rozkładem specjalnym
jest rozkładem specjalnym
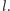
Dowód. Na początek zauważmy, że liczby
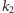 i
i
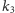 są
pierwsze lub nie większe niż
są
pierwsze lub nie większe niż
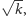 więc są pierwsze lub nie większe
niż
więc są pierwsze lub nie większe
niż
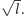 Musimy wobec tego zająć się tylko liczbą
Musimy wobec tego zająć się tylko liczbą
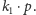 Jeśli
Jeśli
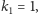 to oczywiście
to oczywiście
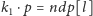 jest liczbą pierwszą.
Załóżmy więc, że
jest liczbą pierwszą.
Załóżmy więc, że
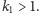 Ponieważ
Ponieważ
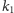 jest dzielnikiem
jest dzielnikiem
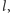 a
a
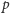 jest najmniejszym (różnym od
jest najmniejszym (różnym od
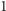 ) dzielnikiem
) dzielnikiem
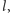 więc
więc
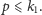 Wobec tego
Wobec tego

a więc
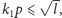 co kończy dowód.
co kończy dowód.
Pozostaje nam jeszcze wykorzystać rozkłady specjalne do efektywnego
obliczania NWD. Tym razem najpierw przedstawimy algorytm, a potem
zastanowimy się nad jego poprawnością. Przyjmiemy, że rozkłady specjalne
zapamiętaliśmy w tablicy
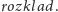
![Algorytm nwd(k, l)
(x1,x2,x3) = rozklad[k];
(y1,y2,y3) = rozklad[l];
g = 1;
foreach i, j∈ {1,2,3}√ do
if max(xi, y j)⩽ n then
d = nwd[xi,yj ];
else if x = y then d = x ;
i j i
elsed = 1;
g = g⋅d;
xi = xi/d;y j = y j/d;
return g;](/math/temat/informatyka/algorytmy/2012/12/28/Najwiekszy_wspolny_dzielnik/1x-8dd9b7a336047c97d0d924fd20091c7faadaed93-dm-33,33,33-FF,FF,FF.gif)
Na początek zauważmy, że w każdym obrocie pętli
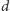 jest pewnym
wspólnym dzielnikiem
jest pewnym
wspólnym dzielnikiem
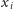 oraz
oraz
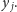 Co więcej,
Co więcej,
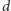 jest
największym wspólnym dzielnikiem
jest
największym wspólnym dzielnikiem
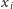 oraz
oraz
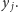 Jeśli
Jeśli
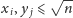 lub
lub
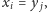 nie mamy co do tego wątpliwości. Bez
straty ogólności niech więc
nie mamy co do tego wątpliwości. Bez
straty ogólności niech więc
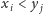 oraz
oraz
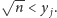 Wówczas
Wówczas
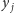 jest liczbą pierwszą, a więc
jest liczbą pierwszą, a więc
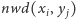 może być
równe
może być
równe
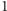 lub
lub
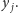 Drugą możliwość natychmiast wyklucza
nierówność
Drugą możliwość natychmiast wyklucza
nierówność
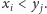
Pozostaje teraz wykazać, że
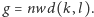 Zrobimy to przez wskazanie
niezmienników pętli:
Zrobimy to przez wskazanie
niezmienników pętli:
-
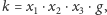
-
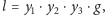
-
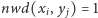 dla już przetworzonych par
dla już przetworzonych par
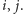
Na ich podstawie wnioskujemy, że po ostatnim obrocie pętli
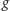 jest
wspólnym dzielnikiem
jest
wspólnym dzielnikiem
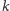 i
i
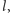 a liczby
a liczby
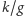 i
i
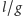 są
względnie pierwsze.
są
względnie pierwsze.
W ten sposób skonstruowaliśmy algorytm, który na
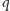 zapytań o NWD
liczb z zakresu
zapytań o NWD
liczb z zakresu
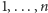 odpowiada w czasie
odpowiada w czasie
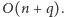 O ile tylko
O ile tylko
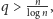 to ten algorytm jest najlepszy z tutaj przedstawionych. Okazuje
się, że w pewien sposób można połączyć jego siły z algorytmem Euklidesa
i otrzymać rozwiązanie, które nigdy nie jest asymptotycznie wolniejsze od
żadnego z zaprezentowanych, a dla pewnych wartości
to ten algorytm jest najlepszy z tutaj przedstawionych. Okazuje
się, że w pewien sposób można połączyć jego siły z algorytmem Euklidesa
i otrzymać rozwiązanie, które nigdy nie jest asymptotycznie wolniejsze od
żadnego z zaprezentowanych, a dla pewnych wartości
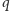 (np.
(np.
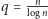 ) jest niemal
) jest niemal
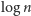 razy szybsze. Stworzenie tego
działającego w czasie
razy szybsze. Stworzenie tego
działającego w czasie
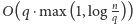 algorytmu pozostawiamy
Czytelnikowi jako zadanie.
algorytmu pozostawiamy
Czytelnikowi jako zadanie.