Informatyczny kącik olimpijski
Dwa przyjęcia
W niedawno wydanej książce W poszukiwaniu wyzwań – zbiorze zadań
z konkursów programistycznych – Filip Wolski opisał rozwiązanie zadania Dwa
przyjęcia z finału XII Olimpiady Informatycznej. W zadaniu tym występuje
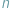 osób, z których niektóre się znają (wiemy które). Chcemy
podzielić ten zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby
zmaksymalizować liczbę osób, które mają parzystą liczbę znajomych na
przyjęciu, na którym przebywają...
osób, z których niektóre się znają (wiemy które). Chcemy
podzielić ten zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby
zmaksymalizować liczbę osób, które mają parzystą liczbę znajomych na
przyjęciu, na którym przebywają...
Przedstawiony w książce algorytm jest efektem indukcyjnego rozumowania o strukturze grafu zbudowanego na bazie relacji znajomości (krawędzie) pomiędzy osobami (wierzchołki) i pokazuje, że zawsze da się podzielić zbiór osób na takie dwie grupy, że każda osoba ma parzystą liczbę znajomych wewnątrz swojej grupy.
Wiedząc o tym, że szukany podział zawsze istnieje, można to zadanie
rozwiązać zupełnie inaczej, bez stosowania teorii grafów. Zauważmy, że
w zasadzie mamy do czynienia jedynie z wartościami binarnymi: są dwa
przyjęcia, każdy gość musi trafić albo na pierwsze, albo na drugie z nich,
wreszcie interesuje nas tylko parzystość liczby znajomych, a nie jej dokładna
wartość. Sprowadzimy zatem oryginalny problem do znalezienia rozwiązania
pewnego układu równań w ciele
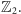
Zaczniemy od przypisania każdej osobie niewiadomej
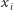 o następującym
znaczeniu:
o następującym
znaczeniu:

Przyjmijmy na chwilę, że
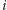 -ta osoba ma znajomych o numerach
-ta osoba ma znajomych o numerach
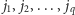 oraz że jest ich parzyście wielu (tj.
oraz że jest ich parzyście wielu (tj.
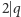 ). Przyjrzyjmy
się takiemu oto równaniu:
). Przyjrzyjmy
się takiemu oto równaniu:
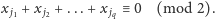 | (1) |
Jeśli znajdziemy wartościowanie niewiadomych
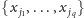 spełniające
to równanie, to wtedy
spełniające
to równanie, to wtedy
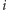 -ta osoba będzie miała tak na pierwszym,
jak i na drugim przyjęciu parzystą liczbę znajomych. W przeciwnym
przypadku na obu przyjęciach będzie nieparzysta liczba znajomych
-ta osoba będzie miała tak na pierwszym,
jak i na drugim przyjęciu parzystą liczbę znajomych. W przeciwnym
przypadku na obu przyjęciach będzie nieparzysta liczba znajomych
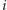 -tej
osoby.
-tej
osoby.
Dla osób o nieparzystej liczbie znajomych będziemy musieli lekko zmodyfikować
nasze rozumowanie. Jeśli bowiem dla takiej osoby
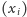 zbudujemy
analogiczne równanie
zbudujemy
analogiczne równanie

to spełniające je wartościowanie niewiadomych
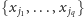 będzie
oznaczało, że
będzie
oznaczało, że
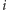 -ta osoba ma parzyście wielu znajomych na pierwszym
przyjęciu i nieparzyście wielu na drugim. Jeśli zamiast zera postawilibyśmy
po prawej stronie równania jedynkę, uzyskalibyśmy analogiczną sytuację:
-ta osoba ma parzyście wielu znajomych na pierwszym
przyjęciu i nieparzyście wielu na drugim. Jeśli zamiast zera postawilibyśmy
po prawej stronie równania jedynkę, uzyskalibyśmy analogiczną sytuację:
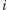 -ta osoba ma parzyście wielu znajomych na drugim przyjęciu
i nieparzyście wielu na pierwszym. W każdym przypadku
-ta osoba ma parzyście wielu znajomych na drugim przyjęciu
i nieparzyście wielu na pierwszym. W każdym przypadku
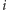 -ta osoba
może „przypadkowo” znaleźć się na przyjęciu z nieparzystą liczbą swoich
znajomych.
-ta osoba
może „przypadkowo” znaleźć się na przyjęciu z nieparzystą liczbą swoich
znajomych.
Aby poradzić sobie z osobami o nieparzyście wielu znajomych, zastosujemy pewną sztuczkę – włączymy takie osoby do równań z ich znajomymi:
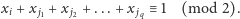 | (2) |
Żeby upewnić się, że taki pomysł ma sens, rozpatrzmy dwa przypadki:
- 1.
- Na pierwszym przyjęciu znajduje się parzyście wielu znajomych
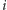 -tej osoby. Wtedy, oczywiście, jest ich nieparzyście wielu
na drugim przyjęciu, a zatem chcemy sprawić, aby
-tej osoby. Wtedy, oczywiście, jest ich nieparzyście wielu
na drugim przyjęciu, a zatem chcemy sprawić, aby
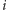 -ta osoba
znalazła się na pierwszym przyjęciu. Ale w takiej sytuacji powyższe
równanie będzie spełnione wtedy i tylko wtedy, gdy
-ta osoba
znalazła się na pierwszym przyjęciu. Ale w takiej sytuacji powyższe
równanie będzie spełnione wtedy i tylko wtedy, gdy
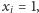 czyli
jest dobrze.
czyli
jest dobrze.
- 2.
- Na pierwszym przyjęciu znajduje się nieparzyście wielu znajomych
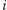 -tej osoby, a na drugim parzyście wielu. Wtedy chcemy wysłać
tę osobę na drugie przyjęcie, więc
-tej osoby, a na drugim parzyście wielu. Wtedy chcemy wysłać
tę osobę na drugie przyjęcie, więc
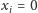 i równanie też zostanie
spełnione.
i równanie też zostanie
spełnione.
Mamy już wszystkie składniki potrzebne do rozwiązania zadania. Konstruujemy
układ
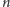 równań – po jednym dla każdej osoby. Jeśli
równań – po jednym dla każdej osoby. Jeśli
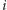 -ta osoba
ma parzyście wielu znajomych, to równanie jest postaci (1), a w przeciwnym
przypadku postaci (2). Na przykład:
-ta osoba
ma parzyście wielu znajomych, to równanie jest postaci (1), a w przeciwnym
przypadku postaci (2). Na przykład:
Do rozwiązywania układów równań liniowych służy algorytm eliminacji Gaussa. Zwykle jednak stosuje się go do „standardowych” układów równań w ciele liczb rzeczywistych, a nie w arytmetyce modularnej. Kluczowymi operacjami w eliminacji Gaussa są działania na wierszach rozszerzonej macierzy reprezentującej układ równań: mnożenie wiersza przez skalar oraz dodawanie wierszy. Za ich pomocą sprowadzamy macierz najpierw do postaci trójkątnej górnej z jedynkami na przekątnej, a następnie pozbywamy się wartości z górnej części macierzy, co daje nam rozwiązanie układu.
Aby przystosować eliminację Gaussa do działania w ciele
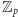 (czyli
w arytmetyce modularnej o podstawie
(czyli
w arytmetyce modularnej o podstawie
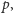 gdzie
gdzie
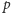 jest liczbą
pierwszą), musimy umieć wykonywać analogiczne operacje. Zazwyczaj nie jest
to duży problem: dodając wiersze, musimy jedynie pamiętać o braniu reszty
z dzielenia przez
jest liczbą
pierwszą), musimy umieć wykonywać analogiczne operacje. Zazwyczaj nie jest
to duży problem: dodając wiersze, musimy jedynie pamiętać o braniu reszty
z dzielenia przez
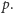 Mnożenie przez skalar działa tak samo. Należy
jednakże pamiętać, że w liczbach rzeczywistych mnożenie zwykle służy
temu, aby doprowadzić do znalezienia się na przekątnej liczby
Mnożenie przez skalar działa tak samo. Należy
jednakże pamiętać, że w liczbach rzeczywistych mnożenie zwykle służy
temu, aby doprowadzić do znalezienia się na przekątnej liczby
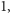 więc
często mnożymy przez jakiś ułamek (de facto wykonujemy dzielenie).
W arytmetyce modularnej o podstawie
więc
często mnożymy przez jakiś ułamek (de facto wykonujemy dzielenie).
W arytmetyce modularnej o podstawie
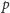 odpowiednikiem takiego
działania będzie przemnożenie
odpowiednikiem takiego
działania będzie przemnożenie
 przez taką liczbę
przez taką liczbę
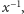 że
że
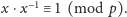 W znajdowaniu takich wartości może pomóc np.
rozszerzony algorytm Euklidesa.
W znajdowaniu takich wartości może pomóc np.
rozszerzony algorytm Euklidesa.
Na szczęście nasze zadanie jest dużo prostsze, wszak działamy w
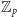 dla
dla
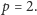 W związku z tym nigdy nie wykonamy mnożenia ani
dzielenia (gdyż jedynym niezerowym skalarem w
W związku z tym nigdy nie wykonamy mnożenia ani
dzielenia (gdyż jedynym niezerowym skalarem w
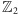 jest jedynka).
Czas i pamięć potrzebne na zbudowanie układu równań są rzędu
jest jedynka).
Czas i pamięć potrzebne na zbudowanie układu równań są rzędu
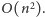 Łączna złożoność czasowa algorytmu wynosi jednak
Łączna złożoność czasowa algorytmu wynosi jednak
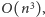 bowiem w takim czasie działa eliminacja Gaussa.
bowiem w takim czasie działa eliminacja Gaussa.