Informatyczny kącik olimpijski
Teleporty
W tej edycji kącika omówimy zadanie pt. Podlewanie ogórków (naprawdę!) z rundy 2A konkursu TopCoder Open 2012.
W zadaniu dany jest pewien zbiór punktów ustawionych wzdłuż prostej
i naszym celem jest odwiedzić wszystkie te punkty w pewnej zadanej kolejności.
Innymi słowy, mamy
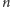 różnych punktów ponumerowanych od
różnych punktów ponumerowanych od
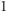 do
do
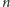 (porządek numerów niekoniecznie od lewej do prawej)
i powinniśmy odwiedzić je wszystkie w kolejności
(porządek numerów niekoniecznie od lewej do prawej)
i powinniśmy odwiedzić je wszystkie w kolejności
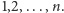 Pomóc
nam w tym mogą teleporty – mamy możliwość rozstawić w dowolnych
punktach prostej łącznie
Pomóc
nam w tym mogą teleporty – mamy możliwość rozstawić w dowolnych
punktach prostej łącznie
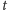 teleportów. Teleporty działają tak, że
w ułamku sekundy możemy teleportować się z dowolnego teleportu do
dowolnego innego teleportu. Naszym zadaniem jest tak ustawić dostępne
teleporty, aby zminimalizować długość trasy odwiedzającej po kolei punkty
teleportów. Teleporty działają tak, że
w ułamku sekundy możemy teleportować się z dowolnego teleportu do
dowolnego innego teleportu. Naszym zadaniem jest tak ustawić dostępne
teleporty, aby zminimalizować długość trasy odwiedzającej po kolei punkty
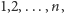 przy założeniu, że po drodze możemy teleportować się
dowolnie wiele razy.
przy założeniu, że po drodze możemy teleportować się
dowolnie wiele razy.
Rozwiązywanie każdego (nietrywialnego) zadania warto rozpocząć od
wstępnej analizy problemu, czyli od stwierdzenia, o co w nim tak naprawdę
chodzi. Niech
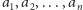 oznaczają współrzędne kolejnych
punktów od lewej do prawej, a
oznaczają współrzędne kolejnych
punktów od lewej do prawej, a
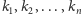 – numery tych punktów.
Niech wreszcie
– numery tych punktów.
Niech wreszcie
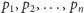 oznaczają współrzędne punktów
w porządku zadanych numerów
oznaczają współrzędne punktów
w porządku zadanych numerów
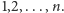 Zauważmy, że
poszukiwaną optymalną ścieżkę możemy podzielić na fragmenty: od
Zauważmy, że
poszukiwaną optymalną ścieżkę możemy podzielić na fragmenty: od
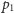 do
do
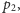 od
od
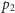 do
do
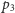 itd., przy czym każdy
z fragmentów biegnie albo w linii prostej między punktami
itd., przy czym każdy
z fragmentów biegnie albo w linii prostej między punktami
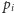 a
a
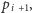 albo ścieżką od punktu
albo ścieżką od punktu
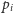 do najbliższego mu
teleportu i od teleportu najbliższego punktowi
do najbliższego mu
teleportu i od teleportu najbliższego punktowi
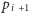 do punktu
do punktu
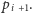
Na pewno warto coś zrobić z faktem, że zgodnie z treścią zadania liczba
możliwych rozstawień teleportów jest nieskończona. Naturalna hipoteza jest
taka, że możemy ograniczyć się do teleportów ustawionych w pewnych
spośród zadanych
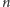 punktów. Łatwo uzasadnić prawdziwość
tej hipotezy: Załóżmy, że pewien teleport znajdowałby się gdzieś
pomiędzy dwoma sąsiednimi punktami, czyli na pozycji
punktów. Łatwo uzasadnić prawdziwość
tej hipotezy: Załóżmy, że pewien teleport znajdowałby się gdzieś
pomiędzy dwoma sąsiednimi punktami, czyli na pozycji
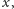 takiej
że
takiej
że
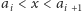 dla pewnego
dla pewnego
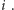 Rozważmy wszystkie
momenty, w których korzystamy z teleportu
Rozważmy wszystkie
momenty, w których korzystamy z teleportu
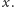 W każdym
z nich musimy dojść do tego teleportu albo od punktu
W każdym
z nich musimy dojść do tego teleportu albo od punktu
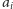 (bądź
innego, położonego na lewo), albo od punktu
(bądź
innego, położonego na lewo), albo od punktu
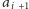 (bądź innego,
położonego na prawo). To oznacza, że odcinek
(bądź innego,
położonego na prawo). To oznacza, że odcinek
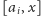 przejdziemy
przejdziemy
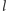 razy, a odcinek
razy, a odcinek
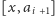 przejdziemy
przejdziemy
 razy. Jeśli więc
razy. Jeśli więc
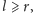 to teleport przestawiamy na pozycję
to teleport przestawiamy na pozycję
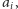 a w przeciwnym
razie na pozycję
a w przeciwnym
razie na pozycję
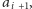 i w obu przypadkach długość trasy nam nie
wzrośnie.
i w obu przypadkach długość trasy nam nie
wzrośnie.
Mamy już jakąś wizję tego, jak będzie wyglądała optymalna trasa oraz
gdzie powinniśmy ustawiać teleporty. To pozwala już skonstruować
pierwsze rozwiązanie zadania, rozpatrujące wszystkie możliwe rozstawienia
teleportów. Złożoność czasowa takiego rozwiązania to z grubsza
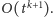
Aby poprawić ten rezultat, powinniśmy jakoś „dobrze uchwycić” nasze zadanie. Problem ewidentnie stanowi w nim obecność dwóch porządków: zadanego porządku odwiedzania punktów oraz naturalnej kolejności „od lewej do prawej”, odpowiadającej najkrótszym ścieżkom między kolejnymi punktami. Potrzebujemy jeszcze jakichś spostrzeżeń.
Załóżmy, że znamy pozycje wszystkich rozstawionych teleportów:
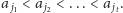 Teleporty te wyznaczałyby wówczas podział
ciągu wszystkich punktów na fragmenty położone między kolejnymi
teleportami. Czy na podstawie tego podziału umielibyśmy łatwo obliczyć
wynik?
Teleporty te wyznaczałyby wówczas podział
ciągu wszystkich punktów na fragmenty położone między kolejnymi
teleportami. Czy na podstawie tego podziału umielibyśmy łatwo obliczyć
wynik?
Rozważmy pewien punkt
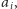 taki że
taki że
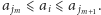 Oznaczmy
Oznaczmy
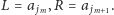 Wiemy, że poprzedni punkt w kolejności
odwiedzania znajduje się na pozycji
Wiemy, że poprzedni punkt w kolejności
odwiedzania znajduje się na pozycji
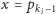 (punkt ten może też nie
istnieć). Jeśli teraz punkt
(punkt ten może też nie
istnieć). Jeśli teraz punkt
 szczęśliwym trafem również znajduje się
między teleportami
szczęśliwym trafem również znajduje się
między teleportami
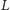 i
i
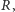 to możemy bardzo łatwo wyznaczyć
najkrótszą ścieżkę między nim a
to możemy bardzo łatwo wyznaczyć
najkrótszą ścieżkę między nim a
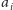 : albo idziemy bezpośrednio po
prostej, albo korzystamy z kombinacji teleportów
: albo idziemy bezpośrednio po
prostej, albo korzystamy z kombinacji teleportów
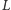 i
i
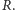 A co,
jeśli punkt
A co,
jeśli punkt
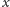 znajduje się zupełnie gdzieś indziej? Wiemy wówczas, że
najkrótsza ścieżka od
znajduje się zupełnie gdzieś indziej? Wiemy wówczas, że
najkrótsza ścieżka od
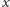 do
do
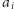 biegnie od
biegnie od
 do
najbliższego mu teleportu i dalej od teleportu najbliższego
do
najbliższego mu teleportu i dalej od teleportu najbliższego
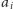 do
do
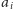 (zauważmy, że jeśli wynikiem jest najkrótsza ścieżka z
(zauważmy, że jeśli wynikiem jest najkrótsza ścieżka z
 do
do
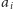 w linii prostej, to i tak możemy ją opisać w podanej
postaci!). To oznacza, że wkład punktu
w linii prostej, to i tak możemy ją opisać w podanej
postaci!). To oznacza, że wkład punktu
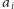 do wyniku możemy
opisać całkiem lokalnie: jeśli mianowicie
do wyniku możemy
opisać całkiem lokalnie: jeśli mianowicie
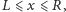 to do wyniku
dodajemy
to do wyniku
dodajemy
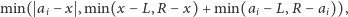 | (1) |
a w przeciwnym razie wynik zwiększamy tylko o
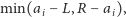 | (2) |
natomiast odległość od punktu
 do najbliższego mu teleportu
dodamy do wyniku w chwili rozpatrywania tego punktu. Aby ta metoda była
poprawna, przy rozpatrywaniu
do najbliższego mu teleportu
dodamy do wyniku w chwili rozpatrywania tego punktu. Aby ta metoda była
poprawna, przy rozpatrywaniu
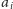 należy jeszcze stwierdzić, czy
następny punkt w kolejności odwiedzania,
należy jeszcze stwierdzić, czy
następny punkt w kolejności odwiedzania,
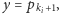 znajduje się
między teleportami
znajduje się
między teleportami
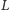 i
i
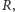 a jeśli nie, jeszcze raz dodać do
wyniku składnik (2). (Jeśli
a jeśli nie, jeszcze raz dodać do
wyniku składnik (2). (Jeśli
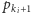 nie istnieje, nie musimy niczego
dodawać).
nie istnieje, nie musimy niczego
dodawać).
To oznacza, że do wyznaczenia wyniku wystarcza nam dla każdego punktu
znajomość pozycji dwóch najbliższych mu teleportów. Możemy więc
zastosować metodę programowania dynamicznego. W ramach stanu
musimy na pewno jakoś zapamiętać zakres rozpatrzonych punktów
wzdłuż prostej, liczbę już ustawionych teleportów oraz pozycje
skrajnych ustawionych teleportów. Najlepiej jest to zrobić tak: pole
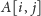 tablicy będzie odpowiadać minimalnej sumie wkładów
punktów
tablicy będzie odpowiadać minimalnej sumie wkładów
punktów
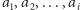 do wyniku, przy założeniu, że rozstawiliśmy
wśród nich
do wyniku, przy założeniu, że rozstawiliśmy
wśród nich
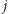 teleportów, z których ostatni znajduje się na pozycji
teleportów, z których ostatni znajduje się na pozycji
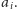 Wówczas ze stanu
Wówczas ze stanu
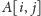 mamy
mamy
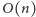 przejść,
do stanów postaci
przejść,
do stanów postaci
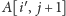 dla
dla
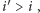 i możemy je
wszystkie rozpatrzyć w czasie
i możemy je
wszystkie rozpatrzyć w czasie
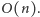 Żeby uniknąć nieprzyjemnych
przypadków brzegowych, postawimy łącznie
Żeby uniknąć nieprzyjemnych
przypadków brzegowych, postawimy łącznie
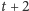 teleporty, z czego
dwa pomocnicze: jeden na pozycji
teleporty, z czego
dwa pomocnicze: jeden na pozycji
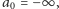 a drugi na pozycji
a drugi na pozycji
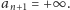
Całe rozwiązanie działa w czasie
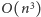 i pamięci
i pamięci