Jeśli chcemy wyznaczyć wszystkie liczby pierwsze nieprzekraczające 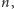 wypisujemy na kartce liczby naturalne od 1 do 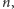 wykreślamy 1, bo nie jest pierwsza, zostawiamy 2 i wykreślamy wszystkie jej wielokrotności, potem zostawiamy 3 i wykreślamy wszystkie jej wielokrotności (niektóre, np. 6, już zostały wykreślone) i tak dalej. W kolejnym kroku pozostawiamy pierwszą niewykreśloną liczbę i wykreślamy jej wielokrotności. Liczby, które nie zostaną wykreślone, to wszystkie liczby pierwsze nie większe od

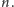
W tym artykule zastanowimy się nad tym, jak szybkie jest sito Eratostenesa. Najczęstszą operacją wykonywaną w tym algorytmie jest wykreślanie.

Za pomocą każdej liczby pierwszej wykreślimy, rzecz jasna, co najwyżej 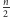 liczb złożonych, wobec czego wykonamy łącznie co najwyżej 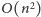 operacji.

Zauważmy, że możemy zakończyć wykreślanie, gdy rozpatrzymy liczby pierwsze od 2 do 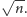 Faktycznie: każda liczba złożona z zakresu od 4 do 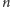 musi mieć jakiś dzielnik pierwszy nie większy niż 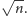 W ten sposób otrzymujemy wariant algorytmu sita działający w czasie

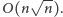
Okazuje się, że możemy uzyskać jeszcze lepsze oszacowanie złożoności czasowej. W tym celu w ogóle nie musimy zmieniać zasady działania algorytmu – wystarczy bardziej precyzyjnie oszacować liczbę wykreśleń. Oznaczmy przez 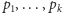 kolejne liczby pierwsze nieprzekraczające 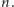 Wówczas łączna liczba wykreśleń to co najwyżej

(*)

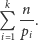Tę sumę możemy oszacować z góry przez

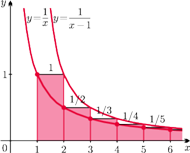
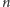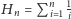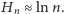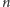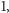
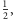
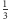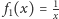Czytelnik Wytrawny dostrzeże w powyższej sumie -tą liczbę harmoniczną  i od razu stwierdzi, że przecież  Można to także sprawdzić, jeśli narysuje się  prostokątów o szerokości 1 i wysokościach kolejno      itd., a także wykresy funkcji i 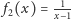 (rysunek ). Wówczas suma pól prostokątów – równa co do wartości liczbie 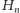 – jest nie mniejsza niż pole pod wykresem funkcji 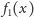 dla 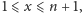 a zatem:

Podobnie, 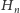 możemy oszacować z góry przez 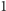 plus pole pod wykresem 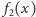 dla 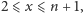 czyli:

W ten sposób wykazaliśmy, że złożoność sita Eratostenesa to 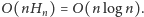 Co ciekawe, można otrzymać jeszcze lepsze oszacowanie, jeśli tylko dokładniej przyjrzeć się sumie 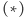 i wykorzystać pewien znany fakt z teorii liczb.

Oznaczmy przez 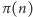 liczbę liczb pierwszych nieprzekraczających liczby 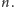 Kluczowy fakt to: 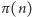 asymptotycznie zachowuje się tak, jak 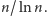 Nie będziemy tego faktu dowodzić. Korzystając z niego, wnioskujemy, że 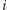-ta liczba pierwsza, 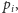 średnio jest rzędu 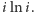 To pozwala nam zapisać sumę 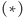 w postaci równoważnej asymptotycznie sumy:

Podobnie jak poprzednio, 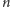-tą część tej sumy możemy asymptotycznie przybliżać całką:

a tę z kolei oszacować z góry przez całkę z prostszym ograniczeniem górnym:

Ostatnią z powyższych całek wyznaczamy przez podstawienie   :

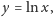
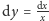W ten sposób otrzymaliśmy asymptotyczne oszacowanie sumy 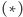 przez funkcję 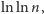 co pozwala stwierdzić, że złożoność sita Eratostenesa to

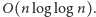
Czytelnik nielubiący manipulować takimi całkami może otrzymać podobnie dobre oszacowania, jeśli tylko spojrzy na algorytm sita z nieco innej strony. Otóż każda liczba złożona między 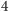 a 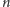 zostanie wykreślona tyle razy, ile ma różnych czynników pierwszych w rozkładzie. Dla liczby całkowitej dodatniej 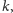 oznaczmy przez 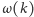 liczbę różnych dzielników pierwszych liczby

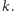
Łatwo wykazać, że zawsze 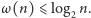 Faktycznie, jeśli 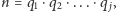 przy czym wszystkie liczby 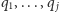 są pierwsze, to 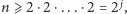 skąd 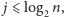 więc tym bardziej 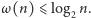 W ten sposób łatwo uzasadniliśmy, że łączna liczba wykreśleń jest rzędu 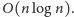 Niestety, tą metodą trudniej jest dojść do lepszego z wcześniejszych oszacowań, tj.

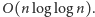
Metodę sita możemy jeszcze trochę usprawnić. Zauważmy, że za pomocą danej liczby pierwszej 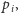 nie większej od 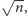 wystarczy wykreślać liczby złożone począwszy od 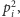 gdyż wszystkie wcześniejsze wielokrotności 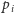 musiały zostać wykreślone wcześniej. Taka poprawka nie zmienia jednak złożoności czasowej algorytmu.

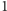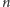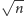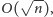Na koniec warto wspomnieć, że w algorytmie sita Eratostenesa cały zakres liczb od  do  możemy podzielić na kawałki długości  i wykreślać liczby złożone tylko w takich kawałkach. To pozwala nam zredukować rozmiar tablicy używanej do wykreślania do wartości rzędu  co ma niebagatelne znaczenie tak teoretyczne, jak i praktyczne. Więcej na ten temat można znaleźć w artykule Tomasza Idziaszka ,,Kolejność ma znaczenie" z Delty 9/2011.